Методы и виды криптографии и шифрования для начинающих — журнал «Рутвет»
Оглавление:
- Методы криптографии
- Виды криптографии
- Криптография для начинающих
Люди еще в древности научились защищать информацию методом её преобразования, чтобы посторонние лица не имели возможности её прочитать. Криптография возникла приблизительно тогда, когда люди только научились разговаривать. Более того, первое время письменность сама по себе представляла криптографическую систему, поскольку ею могли владеть только избранные люди, которым было доступно изучение криптографии.
Методы криптографии
Криптографическим методом защиты информации называется ряд специальных методов кодирования, шифрования или иных преобразований информации, которые позволяют сделать её содержание недоступным для лиц, не обладающих ключом криптограммы. Криптография и шифрование являются самыми надёжными методами защиты, поскольку шифровальщик охраняет непосредственно саму информацию, а не доступ к ней. К примеру, прочтение зашифрованного файла будет невозможным, если даже злоумышленнику удастся похитить носитель. Реализация данного метода защиты осуществляется с помощью программ или пакетов программ.
 Для многих обывателей термин «криптография» означает что-то загадочное и таинственное. Однако в настоящее время различные виды шифрования можно встретить буквально везде — это и простые кодовые замки на дипломатах, и многоуровневые системы защиты секретных файлов. Люди сталкиваются с ней, когда вставляют в банкомат карточку, совершают денежные переводы, покупают через интернет товары, общаются по Skype, отправляют письма на электронную почту. Любые дела, связанные с информацией, так или иначе имеют отношение к криптографии.
Для многих обывателей термин «криптография» означает что-то загадочное и таинственное. Однако в настоящее время различные виды шифрования можно встретить буквально везде — это и простые кодовые замки на дипломатах, и многоуровневые системы защиты секретных файлов. Люди сталкиваются с ней, когда вставляют в банкомат карточку, совершают денежные переводы, покупают через интернет товары, общаются по Skype, отправляют письма на электронную почту. Любые дела, связанные с информацией, так или иначе имеют отношение к криптографии.
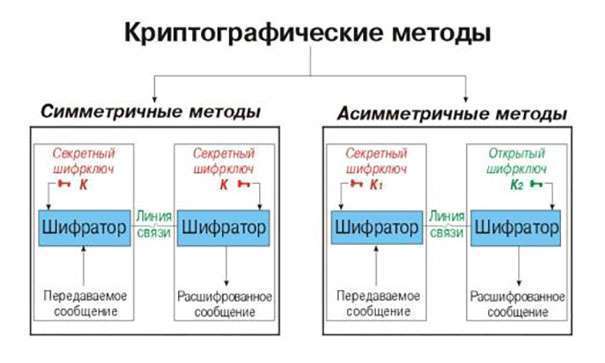
Но, несмотря на всё многообразие сфер применения, в настоящее время существует всего несколько способов шифрования. Все эти методы криптографии относятся к двум видам криптографических систем: симметричным (с секретным ключом) и ассиметричным (с открытым ключом).
- Симметричные системы позволяют шифровать и расшифровывать информацию с помощью одного и того же ключа. Расшифровать криптографическую систему секретного ключа невозможно, если дешифровщик не обладает секретным ключом.
- В криптографических системах с открытым ключом пользователи обладают собственным открытым и частным закрытым ключами. К открытому ключу имеют доступ все пользователи, и информация шифруется именно с его помощью. А вот для расшифровки необходим частный ключ, находящийся у конечного пользователя. В отличие от криптограмм с секретным ключом в такой системе участниками являются не две, а три стороны. Третья может представлять собой сотового провайдера или, например, банк. Однако эта сторона не заинтересована в хищении информации, поскольку она заинтересована в правильном функционировании системы и получении положительных результатов.
Виды криптографии
Достоинством любого современного криптографического метода можно назвать возможность обеспечения высокой гарантированной стойкости защиты, рассчитываемой и выражаемой в числовой форме (среднее число операций или время, необходимое для расшифровки секретной информации или подбора ключей). В настоящее время существуют следующие виды криптографии:
- Шифрование информации.
- Кодирование информации.
- Рассечение информации.
- Сжатие данных.
Видео о криптографии и шифровании
Шифрование
В процессе шифрования в шифруемом сообщении выполняется криптографическое преобразование каждого символа. Среди всех известных способов шифрования можно выделить следующие пять основных групп:
- Замена (подстановка). В свою очередь, различают простую (одноалфавитную), многоалфавитную одноконтурную обыкновенную, многоалфавитную многоконтурную и многоалфавитную одноконтурную монофоническую замены.
- Перестановка. Различают простую, усложнённую по таблице и усложнённую по маршрутам перестановки.
- Аналитические преобразования — осуществляются по особым зависимостям или с помощью правил алгебры матриц.
- Гаммирование — шифрование выполняется с помощью короткой или длинной конечных гамм или с помощью бесконечной гаммы.
- Комбинированные — сообщения шифруются методами замены и перестановки, замены и гаммирования, перестановки и гаммирования или двойного гаммирования.
Кодирование сообщений
В данном типе криптопреобразований используется замена некоторых элементов данных определёнными кодами (к примеру, это могут быть сочетания цифр и/или букв).
Рассечение информации
В этом методе защищаемая информация разделяется на отдельные массивы данных, при расшифровке лишь одного из которых будет невозможно раскрытие засекреченной информации.
Сжатие сообщения
Способ сжатия предусматривает замену в защищаемых данных повторяющимися последовательностями символов на меньшие по размерам последовательности. Эффективность такого сжатия зависит от количества одинаковых последовательностей в защищаемом тексте.
Криптография для начинающих
На протяжении всей многовековой истории криптографии и до настоящего времени это искусство было доступно далеко не каждому. Как правило, эти методы использовали люди, не выходящие за границы резиденций глав держав, посольств, органов разведки. И только несколько десятков лет назад начали происходить кардинальные изменения в этой области — информация стала самостоятельной коммерческой ценностью и превратилась в широко распространённый, почти обычный товар. Её производят, хранят, передают, продают, покупают, а, соответственно — воруют и подделывают. Именно поэтому сегодня существует большое количество учебных пособий и компьютерных программ, предназначенных для обычных пользователей, которым интересна криптография. Обучение некоторым простым видам шифрования может освоить даже школьник.
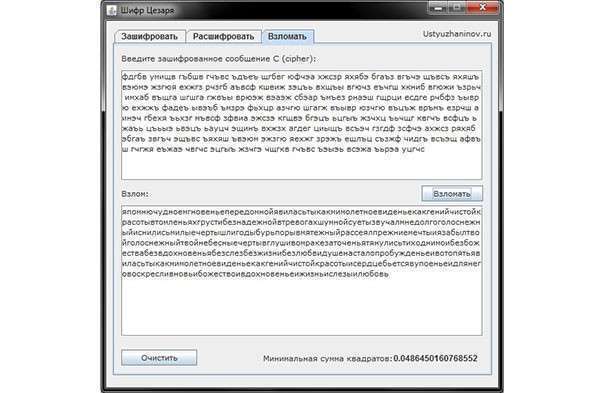
Программа «Шифр Цезаря»
Данный метод шифрования также называют и шифром сдвига. В программном варианте шифр Цезаря представляет собой шифр подстановки с ключом, символы которого заменяются в тексте символами, находящимися на некоторых постоянных числах позиций слева или справа от него в алфавите. К примеру, шифр со сдвигом в правую сторону на три позиции: буква А заменяется на букву Г, Б — на Д и т. д. Следует учитывать, что буква Ё не используется в зашифровке и заменяется буквой Е.
Программа:
 Зашифровка:
Зашифровка:
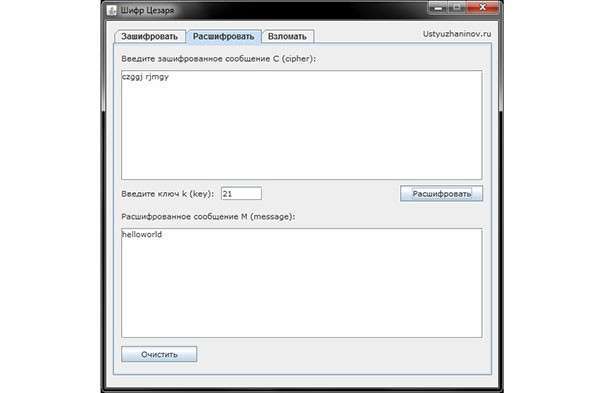
Расшифровка:
А Вас увлекает криптография? Разбираетесь ли Вы в ней? Расскажите об этом в комментариях.
Видео о криптографии для начинающих
9.2. Основные виды шифрования
Б
15
ольшинство средств защиты информации базируется на использовании криптографических шифров и процедур шифрования-расшифрования. В соответствии со стандартом ГОСТ 28147-89 под шифром понимают совокупность обратимых преобразований множества открытых данных на множество зашифрованных данных, задаваемых ключом и алгоритмом криптографического преобразования.Ключ – это конкретное секретное состояние некоторых параметров алгоритма криптографического преобразования данных, обеспечивающее выбор только одного варианта из всех возможных для данного алгоритма /1/.
Основной характеристикой шифра является криптостойкость, которая определяет его стойкость к раскрытию методами криптоанализа. Обычно эта характеристика определяется интервалом времени, необходимым для раскрытия шифра.
К шифрам, используемым для криптографической защиты информации, предъявляется ряд требований:
В той или иной мере этим требованиям отвечают:
Ш
16
ифрование перестановкойзаключается в том, что символы шифруемого текста переставляются по определенному правилу в пределах некоторого блока этого текста. При достаточной длине блока, в пределах которого осуществляется перестановка, и сложном неповторяющемся порядке перестановки можно достигнуть приемлемой для простых практических приложений стойкости шифра.Шифрование заменой (подстановкой)заключается в том, что символы шифруемого текста заменяются символами того же или другого алфавита в соответствии с заранее обусловленной схемой замены.
Шифрование гаммированиемзаключается в том, что символы шифруемого текста складываются с символами некоторой случайной последовательности, именуемойгаммой шифра. Стойкость шифрования определяется в основном длиной (периодом) неповторяющейся части гаммы шифра. Поскольку с помощью ЭВМ можно генерировать практически бесконечную гамму шифра, то данный способ является одним из основных для шифрования информации в автоматизированных системах.
Шифрование аналитическим преобразованиемзаключается в том, что шифруемый текст преобразуется по некоторому аналитическому правилу (формуле).
Например, можно использовать правило умножения вектора на матрицу, причем умножаемая матрица является ключом шифрования (поэтому ее размер и содержание должны храниться в секрете), а символами умножаемого вектора последовательно служат символы шифруемого текста. Другим примером может служить использование так называемых однонаправленных функций для построения криптосистем с открытым ключом.
П
17
о мнению К. Шеннона /5/, в практических шифрах необходимо использовать два основных общих принципа: рассеивание и перемешивание.Рассеиваниепредставляет собой распространение влияния одного знака открытого текста на много знаков шифртекста, что позволяет скрыть статистические свойства открытого текста.
Перемешиваниепредполагает использование таких шифрующих преобразований, которые усложняют восстановление взаимосвязи статистических свойств открытого и шифрованного текстов. Однако шифр должен не только затруднять раскрытие, но и обеспечивать легкость зашифрования и расшифрования при известном пользователю секретном ключе.
Распространенным способом достижения эффектов рассеивания и перемешивания является использование составного шифра, т.е. такого шифра, который может быть реализован в виде некоторой последовательности простых шифров, каждый из которых вносит свой вклад в значительное суммарное рассеивание и перемешивание.
В составных шифрах в качестве простых шифров чаще всего используются простые перестановки и подстановки. При перестановкепросто перемешивают символы открытого текста, причем конкретный вид перемешивания определяется секретным ключом. Приподстановкекаждый символ открытого текста заменяют другим символом из того же алфавита, а конкретный вид подстановки также определяется секретным ключом. Следует заметить, что в современном блочном шифре блоки открытого текста и шифртекста представляют собой двоичные последовательности обычно длиной 64 бита. В принципе каждый блок может принимать 264значений. Поэтому подстановки выполняются в очень большом алфавите, содержащем до 2641019«символов».
П
18
ри многократном чередовании простых перестановок и подстановок, управляемых достаточно длинным секретным ключом, можно получить очень стойкий шифр с хорошим рассеиванием и перемешиванием. Рассмотренные ниже криптоалгоритмы DES, IDEA и отечественный стандарт шифрования данных построен в полном соответствии с указанной методологией.Шифр — Википедия
Материал из Википедии — свободной энциклопедии

Шифр (от фр. chiffre «цифра» от араб. صِفْر, sifr «ноль») — система обратимых преобразований, зависящая от некоторого секретного параметра (ключа) и предназначенная для обеспечения секретности передаваемой информации.
Шифры применяются для тайной переписки дипломатических представителей со своими правительствами, в вооружённых силах для передачи текста секретных документов по техническим средствам связи, банками для обеспечения безопасности транзакций, а также некоторыми интернет-сервисами по различным причинам.
Шифр может представлять собой совокупность условных знаков (условная азбука из цифр, букв или определённых знаков) либо алгоритм преобразования обычных цифр и букв. Процесс засекречивания сообщения с помощью шифра называется шифрованием. Наука о создании и использовании шифров называется криптографией. Криптоанализ — наука о методах получения исходного значения зашифрованной информации.
Важным параметром любого шифра является ключ — параметр криптографического алгоритма, обеспечивающий выбор одного преобразования из совокупности преобразований, возможных для этого алгоритма. В современной криптографии предполагается, что вся секретность криптографического алгоритма сосредоточена в ключе, но не деталях самого алгоритма (принцип Керкгоффса).
Не стоит путать шифр с кодированием — фиксированным преобразованием информации из одного вида в другой. В последнем отсутствует понятие ключа и не выполняется принцип Керкгоффса. В наше время кодирование практически не используется для защиты информации от несанкционированного доступа, а лишь от ошибок при передаче данных (помехоустойчивое кодирование) и других целях, не связанных с защитой.
Шифры могут использовать один ключ для шифрования и расшифрования или два различных ключа. По этому признаку различают:
Шифры могут быть сконструированы так, чтобы либо шифровать сразу весь текст, либо шифровать его по мере поступления. Таким образом существуют:
- Блочный шифр шифрует сразу целый блок текста, выдавая шифротекст после получения всей информации.
- Поточный шифр шифрует информацию и выдаёт шифротекст по мере поступления, таким образом имея возможность обрабатывать текст неограниченного размера, используя фиксированный объём памяти.
Естественно, что блочный шифр можно превратить в поточный, разбивая входные данные на отдельные блоки и шифруя их по отдельности.
Также существуют неиспользуемые сейчас подстановочные шифры, обладающие (в своём большинстве) слабой криптостойкостью.
Асимметричный шифр — система шифрования и/или электронной цифровой подписи (ЭЦП), при которой открытый ключ передаётся по открытому (то есть незащищённому, доступному для наблюдения) каналу, и используется для проверки ЭЦП и для шифрования сообщения. Для генерации ЭЦП и для расшифровки сообщения используется секретный ключ.[1] Криптографические системы с открытым ключом в настоящее время широко применяются в различных сетевых протоколах, в частности, в протоколах TLS и его предшественнике SSL (лежащих в основе HTTPS), в SSH. Также используется в PGP, S/MIME.
Блочные шифры[править | править код]
Поточные шифры[править | править код]
- ↑ Брюс Шнайер. Прикладная криптография. 2-е изд. Протоколы, алгоритмы и исходные тексты на языке Си. Глава 2.7 Цифровые подписи и шифрование.
Криптосистема с открытым ключом — Википедия
Криптографическая система с открытым ключом (разновидность асимметричного шифрования, асимметричного шифра) — система шифрования и/или электронной подписи (ЭП), при которой открытый ключ передаётся по открытому (то есть незащищённому, доступному для наблюдения) каналу и используется для проверки ЭП и для шифрования сообщения. Для генерации ЭП и для расшифровки сообщения используется закрытый ключ[1]. Криптографические системы с открытым ключом в настоящее время широко применяются в различных сетевых протоколах, в частности, в протоколах TLS и его предшественнике SSL (лежащих в основе HTTPS), в SSH. Также используется в PGP, S/MIME.
Идея криптосистемы с открытым ключом[править | править код]
Общие принципы[править | править код]
Асимметричное шифрование с открытым ключом базируется на следующих принципах:
- Можно сгенерировать пару очень больших чисел (открытый ключ и закрытый ключ) так, чтобы, зная открытый ключ, нельзя было вычислить закрытый ключ за разумный срок. При этом механизм генерации является общеизвестным.
- Имеются надёжные методы шифрования, позволяющие зашифровать сообщение открытым ключом так, чтобы расшифровать его можно было только закрытым ключом. Механизм шифрования является общеизвестным.
- Владелец двух ключей никому не сообщает закрытый ключ, но передает открытый ключ контрагентам или делает его общеизвестным.
Если необходимо передать зашифрованное сообщение владельцу ключей, то отправитель должен получить открытый ключ. Отправитель шифрует свое сообщение открытым ключом получателя и передает его получателю (владельцу ключей) по открытым каналам. При этом расшифровать сообщение не может никто, кроме владельца закрытого ключа.
В результате можно обеспечить надёжное шифрование сообщений, сохраняя ключ расшифровки секретным для всех — даже для отправителей сообщений.
Реализация через одностороннюю функцию[править | править код]
Идея криптографии с открытым ключом очень тесно связана с идеей односторонних функций, то есть таких функций f(x){\displaystyle f(x)}, что по известному x{\displaystyle x} довольно просто найти значение f(x){\displaystyle f(x)}, тогда как определение x{\displaystyle x} из f(x){\displaystyle f(x)} невозможно за разумный срок.
Но сама односторонняя функция бесполезна в применении: ею можно зашифровать сообщение, но расшифровать нельзя. Поэтому криптография с открытым ключом использует односторонние функции с лазейкой. Лазейка — это некий секрет, который помогает расшифровать. То есть существует такой y{\displaystyle y}, что зная f(x){\displaystyle f(x)} и y{\displaystyle y}, можно вычислить x{\displaystyle x}. Например, если разобрать часы на множество составных частей, то очень сложно собрать вновь работающие часы. Но если есть инструкция по сборке (лазейка), то можно легко решить эту проблему.
Получатель информации формирует открытый ключ и «лазейку» (другими словами, открытую и закрытую часть ключа), затем передает открытый ключ отправителю, а «лазейку» оставляет у себя. Отправитель шифрует информацию на основе открытого ключа: такую зашифрованную информацию просто расшифровать, лишь имея одновременно и открытый ключ, и «лазейку». В терминах функции, получатель формирует f(){\displaystyle f()} с лазейкой y{\displaystyle y}, затем передает информацию о параметрах функции f(){\displaystyle f()} отправителю (при этом, даже зная параметры функции f(){\displaystyle f()}, невозможно обнаружить «лазейку» за разумный срок). После этого отправитель формирует шифрованное сообщение f(x){\displaystyle f(x)}, а получатель извлекает x{\displaystyle x} из f(x){\displaystyle f(x)}, зная y{\displaystyle y}.
Примеры[править | править код]
Понять идеи и методы криптографии с открытым ключом помогает следующий пример — хранение паролей в удалённом компьютере, к которому должны подключаться пользователи. Каждый пользователь в сети имеет свой пароль. При входе он указывает имя и вводит секретный пароль. Но если хранить пароль на диске удалённого компьютера, то кто-нибудь его может считать (особенно легко это сделать администратору этого компьютера) и получить доступ к секретной информации. Для решения задачи используется односторонняя функция. При создании секретного пароля в компьютере сохраняется не сам пароль, а результат вычисления функции от этого пароля и имени пользователя. Например, пользователь Алиса придумала пароль «Гладиолус». При сохранении этих данных вычисляется результат функции f{\displaystyle f}(АЛИСА_ГЛАДИОЛУС), пусть результатом будет строка РОМАШКА, которая и будет сохранена в системе. В результате файл паролей примет следующий вид:
| Имя | f{\displaystyle f}(имя_пароль) |
|---|---|
| АЛИСА | РОМАШКА |
| БОБ | НАРЦИСС |
Вход в систему теперь выглядит так:
| Имя: | АЛИСА |
|---|---|
| Пароль: | ГЛАДИОЛУС |
Когда Алиса вводит «секретный» пароль, компьютер проверяет, даёт или нет функция, применяемая к АЛИСА_ГЛАДИОЛУС, правильный результат РОМАШКА, хранящийся на диске компьютера. Стоит изменить хотя бы одну букву в имени или в пароле, и результат функции будет совершенно другим. «Секретный» пароль не хранится в компьютере ни в каком виде. Файл паролей может быть теперь просмотрен другими пользователями без потери секретности, так как функция практически необратимая.
В предыдущем примере используется односторонняя функция без лазейки, поскольку не требуется по зашифрованному сообщению получить исходное. В следующем примере рассматривается схема с возможностью восстановить исходное сообщение с помощью «лазейки», то есть труднодоступной информации. Для шифрования текста можно взять большой абонентский справочник, состоящий из нескольких толстых томов (по нему очень легко найти номер любого жителя города, но почти невозможно по известному номеру найти абонента). Для каждой буквы из шифруемого сообщения выбирается имя, начинающееся на ту же букву. Таким образом букве ставится в соответствие номер телефона абонента. Отправляемое сообщение, например «КОРОБКА», будет зашифровано следующим образом:
| Сообщение | Выбранное имя | Криптотекст |
|---|---|---|
| К | Королёв | 5643452 |
| О | Орехов | 3572651 |
| Р | Рузаева | 4673956 |
| O | Осипов | 3517289 |
| Б | Батурин | 7755628 |
| К | Кирсанова | 1235267 |
| А | Арсеньева | 8492746 |
Криптотекстом будет являться цепочка номеров, записанных в порядке их выбора в справочнике. Чтобы затруднить расшифровку, следует выбирать случайные имена, начинающиеся на нужную букву. Таким образом исходное сообщение может быть зашифровано множеством различных списков номеров (криптотекстов).
Примеры таких криптотекстов:
| Криптотекст 1 | Криптотекст 2 | Криптотекст 3 |
|---|---|---|
| 1235267 | 5643452 | 1235267 |
| 3572651 | 3517289 | 3517289 |
| 4673956 | 4673956 | 4673956 |
| 3517289 | 3572651 | 3572651 |
| 7755628 | 7755628 | 7755628 |
| 5643452 | 1235267 | 5643452 |
| 8492746 | 8492746 | 8492746 |
Чтобы расшифровать текст, надо иметь справочник, составленный согласно возрастанию номеров. Этот справочник является лазейкой (секрет, который помогает получить начальный текст), известной только получателю. Без данных из обоих справочников расшифровать текст в общем случае невозможно, однако для шифровки достаточно лишь первого справочника[2]. При этом получатель может заранее легко сформировать оба справочника, передав лишь первый из них отправителю для шифровки.
Пусть K{\displaystyle K} — пространство ключей, а e{\displaystyle e} и d{\displaystyle d} — ключи шифрования и расшифрования соответственно. Ee{\displaystyle E_{e}} — функция шифрования для произвольного ключа e{\displaystyle e}∈{\displaystyle \in }K{\displaystyle K}, такая что:
Ee(m)=c{\displaystyle E_{e}(m)=c}
Здесь c{\displaystyle c}∈{\displaystyle \in }C{\displaystyle C}, где C{\displaystyle C} — пространство шифротекстов, а m{\displaystyle m}∈{\displaystyle \in }M{\displaystyle M}, где M{\displaystyle M} — пространство сообщений.
Dd{\displaystyle D_{d}} — функция расшифрования, с помощью которой можно найти исходное сообщение m{\displaystyle m}, зная шифротекст c{\displaystyle c} :
Dd(c)=m{\displaystyle D_{d}(c)=m}
{Ee{\displaystyle E_{e}}: e{\displaystyle e}∈{\displaystyle \in }K{\displaystyle K}} — набор шифрования, а {Dd{\displaystyle D_{d}}: d{\displaystyle d}∈{\displaystyle \in }K{\displaystyle K}} — соответствующий набор для расшифрования. Каждая пара (E,D){\displaystyle (E,D)} имеет свойство: зная Ee{\displaystyle E_{e}}, невозможно решить уравнение Ee(m)=c{\displaystyle E_{e}(m)=c}, то есть для данного произвольного шифротекста c{\displaystyle c}∈{\displaystyle \in }C{\displaystyle C}, невозможно найти сообщение m{\displaystyle m}∈{\displaystyle \in }M{\displaystyle M}. Это значит, что по данному e{\displaystyle e} невозможно определить соответствующий ключ расшифрования d{\displaystyle d}. Ee{\displaystyle E_{e}} является односторонней функцией, а d{\displaystyle d} — лазейкой[3].
Ниже показана схема передачи информации лицом А лицу В. Они могут быть как физическими лицами, так и организациями и так далее. Но для более лёгкого восприятия принято участников передачи отождествлять с людьми, чаще всего именуемыми Алиса и Боб. Участника, который стремится перехватить и расшифровать сообщения Алисы и Боба, чаще всего называют Евой.
- Боб выбирает пару (e,d){\displaystyle (e,d)} и шлёт ключ шифрования e{\displaystyle e} (открытый ключ) Алисе по открытому каналу, а ключ расшифрования d{\displaystyle d} (закрытый ключ) защищён и секретен (он не должен передаваться по открытому каналу).
- Чтобы послать сообщение m{\displaystyle m} Бобу, Алиса применяет функцию шифрования, определённую открытым ключом e{\displaystyle e}: Ee(m)=c{\displaystyle E_{e}(m)=c}, c{\displaystyle c} — полученный шифротекст.
- Боб расшифровывает шифротекст c{\displaystyle c}, применяя обратное преобразование Dd{\displaystyle D_{d}}, однозначно определённое значением d{\displaystyle d}.
Начало асимметричным шифрам было положено в работе «Новые направления в современной криптографии» Уитфилда Диффи и Мартина Хеллмана, опубликованной в 1976 году. Находясь под влиянием работы Ральфа Меркла о распространении открытого ключа, они предложили метод получения секретных ключей, используя открытый канал. Этот метод экспоненциального обмена ключей, который стал известен как обмен ключами Диффи — Хеллмана, был первым опубликованным практичным методом для установления разделения секретного ключа между заверенными пользователями канала. В 2002 году Хеллман предложил называть данный алгоритм «Диффи — Хеллмана — Меркле», признавая вклад Меркле в изобретение криптографии с открытым ключом. Эта же схема была разработана Малькольмом Вильямсоном (англ. Malcolm J. Williamson) в 1970-х, но держалась в секрете до 1997 года. Метод Меркле по распространению открытого ключа был изобретён в 1974 и опубликован в 1978 году, его также называют загадкой Меркле.
В 1977 году учёными Рональдом Ривестом, Ади Шамиром и Леонардом Адлеманом из Массачусетского технологического института был разработан алгоритм шифрования, основанный на проблеме разложения на множители. Система была названа по первым буквам их фамилий (RSA — Rivest, Shamir, Adleman). Эта же система была изобретена в 1973 году Клиффордом Коксом (англ. Clifford Cocks), работавшим в центре правительственной связи (GCHQ), но эта работа хранилась лишь во внутренних документах центра, поэтому о её существовании не было известно до 1977 года. RSA стал первым алгоритмом, пригодным и для шифрования, и для цифровой подписи.
Вообще, в основу известных асимметричных криптосистем кладётся одна из сложных математических проблем, которая позволяет строить односторонние функции и функции-лазейки. Например, криптосистемы Меркля — Хеллмана и Хора — Ривеста опираются на так называемую задачу об укладке рюкзака.
Основные принципы построения криптосистем с открытым ключом[править | править код]
- Начинаем с трудной задачи P{\displaystyle P}. Она должна решаться сложно в смысле теории: не должно быть алгоритма, с помощью которого можно было бы перебрать все варианты решения задачи P{\displaystyle P} за полиномиальное время относительно размера задачи. Более правильно сказать: не должно быть известного полиномиального алгоритма, решающего данную задачу — так как ни для одной задачи ещё пока не доказано, что для неё подходящего алгоритма нет в принципе.
- Можно выделить легкую подзадачу P′{\displaystyle P’} из P{\displaystyle P}. Она должна решаться за полиномиальное время и лучше, если за линейное.
- «Перетасовываем и взбалтываем» P′{\displaystyle P’}, чтобы получить задачу P″{\displaystyle P»}, совершенно не похожую на первоначальную. Задача P″{\displaystyle P»} должна по крайней мере выглядеть как оригинальная труднорешаемая задача P{\displaystyle P}.
- P″{\displaystyle P»} открывается с описанием, как она может быть использована в роли ключа зашифрования. Как из P″{\displaystyle P»} получить P′{\displaystyle P’}, держится в секрете как секретная лазейка.
- Криптосистема организована так, что алгоритмы расшифрования для легального пользователя и криптоаналитика существенно различны. В то время как второй решает P″{\displaystyle P»}-задачу, первый использует секретную лазейку и решает P′{\displaystyle P’}-задачу.
Криптография с несколькими открытыми ключами[править | править код]
- В следующем примере показана схема, в которой Алиса шифрует сообщение так, что только Боб может прочитать его, и наоборот, Боб шифрует сообщение так, что только Алиса может расшифровать его.
Пусть есть 3 ключа KA{\displaystyle K_{A}}, KB{\displaystyle K_{B}}, KC{\displaystyle K_{C}}, распределенные так, как показано в таблице.
Тогда Алиса может зашифровать сообщение ключом KA{\displaystyle K_{A}}, а Эллен расшифровать ключами KB{\displaystyle K_{B}}, KC{\displaystyle K_{C}}, Кэрол — зашифровать ключом KC{\displaystyle K_{C}}, а Дэйв расшифровать ключами KA{\displaystyle K_{A}}, KB{\displaystyle K_{B}}. Если Дэйв зашифрует сообщение ключом KA{\displaystyle K_{A}}, то сообщение сможет прочитать Эллен, если ключом KB{\displaystyle K_{B}}, то его сможет прочитать Франк, если же обоими ключами KA{\displaystyle K_{A}} и KB{\displaystyle K_{B}}, то сообщение прочитает Кэрол. По аналогии действуют и другие участники. Таким образом, если используется одно подмножество ключей для шифрования, то для расшифрования требуются оставшиеся ключи множества. Такую схему можно использовать для n ключей.
- Теперь можно посылать сообщения группам агентов, не зная заранее состав группы.
Рассмотрим для начала множество, состоящее из трех агентов: Алисы, Боба и Кэрол. Алисе выдаются ключи KA{\displaystyle K_{A}} и KB{\displaystyle K_{B}}, Бобу — KB{\displaystyle K_{B}} и KC{\displaystyle K_{C}}, Кэрол — KA{\displaystyle K_{A}} и KC{\displaystyle K_{C}}. Теперь, если отправляемое сообщение зашифровано ключом KC{\displaystyle K_{C}}, то его сможет прочитать только Алиса, последовательно применяя ключи KA{\displaystyle K_{A}}
Криптографическая стойкость — Википедия
Криптографическая стойкость (или криптостойкость) — способность криптографического алгоритма противостоять криптоанализу. Стойким считается алгоритм, успешная атака на который требует от атакующего обладания недостижимым на практике объёмом вычислительных ресурсов или перехваченных открытых и зашифрованных сообщений либо настолько значительных затрат времени на раскрытие, что к его моменту защищённая информация утратит свою актуальность. В большинстве случаев криптостойкость не может быть математически доказана; можно только доказать уязвимости криптографического алгоритма либо (в случае криптосистем с открытым ключом) свести задачу вскрытия алгоритма к некоторой задаче, которая считается вычислительно сложной (то есть доказать, что «взлом» не легче решения этой задачи).
Типы криптостойких систем шифрования[править | править код]
Рассмотрим условия, которым должна удовлетворять криптосистема для надежной защиты информации. Стойкость зашифрованной информации (криптографическая стойкость, или просто стойкость) зависит от возможности несанкционированного чтения данных.
Абсолютно стойкие системы[править | править код]
Об абсолютной стойкости (или теоретической стойкости) говорят в случае, если криптосистема не может быть раскрыта ни теоретически, ни практически даже при наличии у атакующего бесконечно больших вычислительных ресурсов. Доказательство существования абсолютно стойких алгоритмов шифрования было выполнено Клодом Шенноном и опубликовано в работе «Теория связи в секретных системах»[1]. Там же определены требования к такого рода системам:
- ключ генерируется для каждого сообщения (каждый ключ используется только один раз)
- ключ статистически надёжен (то есть вероятности появления каждого из возможных символов равны, символы в ключевой последовательности независимы и случайны)
- длина ключа равна или больше длины сообщения
- исходный (открытый) текст обладает некоторой избыточностью (что является критерием оценки правильности расшифровки)
Стойкость этих систем не зависит от того, какими вычислительными возможностями обладает криптоаналитик. Практическое применение систем, удовлетворяющих требованиям абсолютной стойкости, ограничено соображениями стоимости и удобства пользования.
Шенноном было доказано, что примером абсолютно стойкого алгоритма является шифр Вернама (одноразовый блокнот). Иными словами, корректное использование шифра Вернама не даёт злоумышленнику никакой информации об открытом тексте (любой бит сообщения он может лишь угадать с вероятностью 1/2{\displaystyle 1/2}).
Достаточно стойкие системы[править | править код]
В основном в криптографических системах гражданского назначения применяются практически стойкие или вычислительно стойкие системы. О вычислительной стойкости системы говорят в случае, если потенциальная возможность вскрыть шифр существует, но при выбранных параметрах и ключах шифрования. На практике атакующий на современном этапе развития технологий не может обладать достаточными вычислительными ресурсами для вскрытия шифра за приемлемое время. Стойкость таких систем зависит от того, какими вычислительными возможностями обладает криптоаналитик.
Практическая стойкость таких систем базируется на теории сложности и оценивается исключительно в расчёте на определённый момент времени и последовательно c двух позиций:
В каждом конкретном случае могут существовать дополнительные критерии оценки стойкости.
О доказуемой стойкости говорят в случае, если доказательство стойкости криптосистемы сводится к решению определённой трудно решаемой математической проблемы, положенной в основу алгоритма. Так, криптосистема RSA считается стойкой, если модуль числового преобразования невозможно факторизовать за полиномиальное время.
Оценка криптостойкости систем шифрования[править | править код]
Начальная оценка[править | править код]
Поскольку атака методом грубой силы (полным перебором всех ключей) возможна для всех типов криптографических алгоритмов, кроме абсолютно стойких «по Шеннону», для вновь созданного алгоритма она может являться единственной существующей. Способы её оценки основываются на вычислительной сложности, которая затем может быть выражена во времени, деньгах, и требуемой производительности вычислительных ресурсов, например, в MIPS. Эта оценка пока является максимальной и минимальной одновременно.
Текущая оценка[править | править код]
Дальнейшее исследование алгоритма с целью поиска слабостей (уязвимостей) (криптоанализ) добавляет оценки стойкости по отношению к известным криптографическим атакам (линейный, дифференциальный криптоанализ и др.) и могут понизить известную стойкость.
Например, для многих симметричных шифров существуют слабые ключи[en] и S-блоки, применение которых снижает криптографическую стойкость.
Также важным способом проверки стойкости являются атаки на реализацию, выполняемые для конкретного программно-аппаратно-человеческого комплекса.
Важность длительной проверки и открытого обсуждения[править | править код]
Чем более длительным и экспертным является анализ алгоритма и реализаций, тем более достоверной можно считать его стойкость. В нескольких случаях длительный и внимательный анализ приводил к снижению оценки стойкости ниже приемлемого уровня (например, в черновых версиях FEAL).
Недостаточная проверка (по мнению многих криптографов — искусственное ослабление) алгоритма потокового шифрования А5/1 привела к успешной атаке.
Симметричные криптосистемы — Википедия
Симметри́чные криптосисте́мы (также симметричное шифрование, симметричные шифры) (англ. symmetric-key algorithm) — способ шифрования, в котором для шифрования и расшифровывания применяется один и тот же криптографический ключ. До изобретения схемы асимметричного шифрования единственным существовавшим способом являлось симметричное шифрование. Ключ алгоритма должен сохраняться в тайне обеими сторонами, осуществляться меры по защите доступа к каналу, на всем пути следования криптограммы, или сторонами взаимодействия посредством криптообъектов, сообщений, если данный канал взаимодействия под грифом «Не для использования третьими лицами». Алгоритм шифрования выбирается сторонами до начала обмена сообщениями.
Алгоритмы шифрования данных широко применяются в компьютерной технике в системах сокрытия конфиденциальной и коммерческой информации от злонамеренного использования сторонними лицами. Главным принципом в них является условие, что передатчик и приемник заранее знают алгоритм шифрования, а также ключ к сообщению, без которых информация представляет собой всего лишь набор символов, не имеющих смысла.
Классическими примерами таких алгоритмов являются симметричные криптографические алгоритмы, перечисленные ниже:
- Простая перестановка
- Одиночная перестановка по ключу
- Двойная перестановка
- Перестановка «Магический квадрат»
Простая перестановка[править | править код]
Простая перестановка без ключа — один из самых простых методов шифрования. Сообщение записывается в таблицу по столбцам. После того, как открытый текст записан колонками, для образования шифртекста он считывается по строкам. Для использования этого шифра отправителю и получателю нужно договориться об общем ключе в виде размера таблицы. Объединение букв в группы не входит в ключ шифра и используется лишь для удобства записи несмыслового текста.
Одиночная перестановка по ключу[править | править код]
Более практический метод шифрования, называемый одиночной перестановкой по ключу, очень похож на предыдущий. Он отличается лишь тем, что колонки таблицы переставляются по ключевому слову, фразе или набору чисел длиной в строку таблицы.
Двойная перестановка[править | править код]
Для дополнительной скрытности можно повторно шифровать сообщение, которое уже было зашифровано. Этот способ известен под названием двойная перестановка. Для этого размер второй таблицы подбирают так, чтобы длины её строк и столбцов отличались от длин в первой таблице. Лучше всего, если они будут взаимно простыми. Кроме того, в первой таблице можно переставлять столбцы, а во второй строки. Наконец, можно заполнять таблицу зигзагом, змейкой, по спирали или каким-то другим способом. Такие способы заполнения таблицы если и не усиливают стойкость шифра, то делают процесс шифрования гораздо более занимательным.
Перестановка «Магический квадрат»[править | править код]
Магическими квадратами называются квадратные таблицы со вписанными в их клетки последовательными натуральными числами от 1, которые дают в сумме по каждому столбцу, каждой строке и каждой диагонали одно и то же число. Подобные квадраты широко применялись для вписывания шифруемого текста по приведенной в них нумерации. Если потом выписать содержимое таблицы по строкам, то получалась шифровка перестановкой букв. На первый взгляд кажется, будто магических квадратов очень мало. Тем не менее, их число очень быстро возрастает с увеличением размера квадрата. Так, существует лишь один магический квадрат размером 3 х 3, если не принимать во внимание его повороты. Магических квадратов 4 х 4 насчитывается уже 880, а число магических квадратов размером 5 х 5 около 250000. Поэтому магические квадраты больших размеров могли быть хорошей основой для надежной системы шифрования того времени, потому что ручной перебор всех вариантов ключа для этого шифра был немыслим.
В квадрат размером 4 на 4 вписывались числа от 1 до 16. Его магия состояла в том, что сумма чисел по строкам, столбцам и полным диагоналям равнялась одному и тому же числу — 34. Впервые эти квадраты появились в Китае, где им и была приписана некоторая «магическая сила».
| 16 | 3 | 2 | 13 |
| 5 | 10 | 11 | 8 |
| 9 | 6 | 7 | 12 |
| 4 | 15 | 14 | 1 |
Шифрование по магическому квадрату производилось следующим образом. Например, требуется зашифровать фразу: «ПриезжаюСегодня.». Буквы этой фразы вписываются последовательно в квадрат согласно записанным в них числам: позиция буквы в предложении соответствует порядковому числу. В пустые клетки ставится точка.
| 16. | 3 и | 2 р | 13 д |
| 5 з | 10 е | 11 г | 8 ю |
| 9 С | 6 ж | 7 а | 12 о |
| 4 е | 15 я | 14 н | 1 П |
После этого шифрованный текст записывается в строку (считывание производится слева направо, построчно):
.ирдзегюСжаоеянП
При расшифровывании текст вписывается в квадрат, и открытый текст читается в последовательности чисел «магического квадрата». Программа должна генерировать «магические квадраты» и по ключу выбирать необходимый. Размер квадрата больше чем 3х3.
Полная утрата всех статистических закономерностей исходного сообщения является важным требованием к симметричному шифру. Для этого шифр должен иметь «эффект лавины» — должно происходить сильное изменение шифроблока при 1-битном изменении входных данных (в идеале должны меняться значения 1/2 бит шифроблока).
Также важным требованием является отсутствие линейности (то есть условия f(a) xor f(b) == f(a xor b)), в противном случае облегчается применение дифференциального криптоанализа к шифру.
В настоящее время симметричные шифры — это:
- блочные шифры. Обрабатывают информацию блоками определённой длины (обычно 64, 128 бит), применяя к блоку ключ в установленном порядке, как правило, несколькими циклами перемешивания и подстановки, называемыми раундами. Результатом повторения раундов является лавинный эффект — нарастающая потеря соответствия битов между блоками открытых и зашифрованных данных.
- поточные шифры, в которых шифрование проводится над каждым битом либо байтом исходного (открытого) текста с использованием гаммирования. Поточный шифр может быть легко создан на основе блочного (например, ГОСТ 28147-89 в режиме гаммирования), запущенного в специальном режиме.
Большинство симметричных шифров используют сложную комбинацию большого количества подстановок и перестановок. Многие такие шифры исполняются в несколько (иногда до 80) проходов, используя на каждом проходе «ключ прохода». Множество «ключей прохода» для всех проходов называется «расписанием ключей» (key schedule). Как правило, оно создается из ключа выполнением над ним неких операций, в том числе перестановок и подстановок.
Типичным способом построения алгоритмов симметричного шифрования является сеть Фейстеля. Алгоритм строит схему шифрования на основе функции F(D, K), где D — порция данных размером вдвое меньше блока шифрования, а K — «ключ прохода» для данного прохода. От функции не требуется обратимость — обратная ей функция может быть неизвестна. Достоинства сети Фейстеля — почти полное совпадение дешифровки с шифрованием (единственное отличие — обратный порядок «ключей прохода» в расписании), что значительно облегчает аппаратную реализацию.
Операция перестановки перемешивает биты сообщения по некоему закону. В аппаратных реализациях она тривиально реализуется как перепутывание проводников. Именно операции перестановки дают возможность достижения «эффекта лавины». Операция перестановки линейна — f(a) xor f(b) == f(a xor b)
Операции подстановки выполняются как замена значения некоей части сообщения (часто в 4, 6 или 8 бит) на стандартное, жестко встроенное в алгоритм иное число путём обращения к константному массиву. Операция подстановки привносит в алгоритм нелинейность.
Зачастую стойкость алгоритма, особенно к дифференциальному криптоанализу, зависит от выбора значений в таблицах подстановки (S-блоках). Как минимум считается нежелательным наличие неподвижных элементов S(x) = x, а также отсутствие влияния какого-то бита входного байта на какой-то бит результата — то есть случаи, когда бит результата одинаков для всех пар входных слов, отличающихся только в данном бите.
Существует множество (не менее двух десятков) алгоритмов симметричных шифров, существенными параметрами которых являются:
- стойкость
- длина ключа
- число раундов
- длина обрабатываемого блока
- сложность аппаратной/программной реализации
- сложность преобразования
- блочные шифры
- AES (англ. Advanced Encryption Standard) — американский стандарт шифрования
- ГОСТ 28147-89 — советский и российский стандарт шифрования, также является стандартом СНГ
- DES (англ. Data Encryption Standard) — стандарт шифрования данных в США
- 3DES (Triple-DES, тройной DES)
- RC2 (Шифр Ривеста (Rivest Cipher или Ron’s Cipher))
- RC5
- Blowfish
- Twofish
- NUSH
- IDEA (International Data Encryption Algorithm, международный алгоритм шифрования данных)
- CAST (по инициалам разработчиков Carlisle Adams и Stafford Tavares)
- CRAB
- 3-WAY
- Khufu и Khafre
- Kuznechik
- потоковые шифры
- RC4 (алгоритм шифрования с ключом переменной длины)
- SEAL (Software Efficient Algorithm, программно-эффективный алгоритм)
- WAKE (World Auto Key Encryption algorithm, алгоритм шифрования на автоматическом ключе)
Сравнение с асимметричными криптосистемами[править | править код]
Достоинства[править | править код]
- скорость
- простота реализации (за счёт более простых операций)
- меньшая требуемая длина ключа для сопоставимой стойкости
- изученность (за счёт большего возраста)
Недостатки[править | править код]
- сложность управления ключами в большой сети
- сложность обмена ключами. Для применения необходимо решить проблему надёжной передачи ключей каждому абоненту, так как нужен секретный канал для передачи каждого ключа обеим сторонам
Для компенсации недостатков симметричного шифрования в настоящее время широко применяется комбинированная (гибридная) криптографическая схема, где с помощью асимметричного шифрования передаётся сеансовый ключ, используемый сторонами для обмена данными с помощью симметричного шифрования.
Важным недостатком симметричных шифров является невозможность их использования в механизмах формирования электронной цифровой подписи и сертификатов, так как ключ известен каждой стороне.
- Гатчин Ю. А., Коробейников А. Г. Основы криптографических алгоритмов. Учебное пособие. — СПб.: СПбГИТМО(ТУ), 2002.
- Кон П. Универсальная алгебра. — М.: Мир. — 1968.
- Коробейников А. Г. Математические основы криптографии. Учебное пособие. СПб: СПб ГИТМО (ТУ), 2002.
«Что такое криптография, и где она применяется?» – Яндекс.Знатоки
Криптография — наука о методах изложения о информации, которые скрывают смысл изложенного путём перестановки информационных единиц по определённой системе.
Криптография в переводе с греческого языка означает «скрытное написание»: κρυπτός — «скрытый» и γράφω — «пишу».
Люди, занимающиеся криптографией, называются Криптографы. Специалисты в области вскрытия шифров называются Криптоаналитики.
Наука, объединяющая криптографию и криптоанализ, называется Криптология.
Немного простой математики:
Схематично, математическим языком, элементарный процесс шифрования и дешифрования информации можно выразить так:
- E(P) = C — процесс простого шифрования.
E — функция шифрования.
P — информация для шифрования (обычное сообщение: текст, аудио, видео — любой битовый поток).
C — зашифрованный результат.
- D(C) = P — процесс дешифрования (преобразование зашифрованной информации в простой вид).
D — функция дешифрования.
Таким образом, отношения шифрования и последующего дешифрования информации можно выразить формулой: D(E(P)) = P.
Основные задачи криптографии
Криптография позволяет решить основные задачи по обеспечению: аутентификации, целостности и неоспоримости данных.
- Аутентификация позволяет установить, что сообщение исходит от конкретного отправителя.
- Проверка целостности информации позволяет установить/исключить факт перехвата зашифрованного сообщения и внесения в его содержимое изменений.
- Проверка неоспоримости авторства отправителя сообщения необходима для исключения возможных отрицаний причастности конкретных отправителей к отправленному сообщению.
Гражданское применение криптографии
Криптографические механизмы защиты информации в гражданском обороте применяются для защиты информации составляющей коммерческую тайну, персональные данные граждан и другие виды информации с ограниченным доступом.
Также, в коммерческой и социальной сфере криптографические механизмы в виде электронно-цифровой подписи (ЭЦП) используются для фиксирования результатов и условий заключения договоров.
Криптографические механизмы применяются в программно-аппаратных устройствах, являющихся средствами криптографической защиты информации (СКЗИ).
***
Дополнительные сведения о криптографических устройствах можно узнать на канале «ИНФОРМАЦИОННОЕ ПРАВО в обществе», например, в нарративе Аппаратные средства защиты информации.
5 декабря 2018 г.
дополнительно, статьи о древних шифрах:
автор: Демешин Сергей Владимирович.

