что это такое в математике, операции и действия, как составить, примеры

При решении алгебраических или дифференциальных уравнений студенты сталкиваются с понятием матрицы. Этот термин используется в программировании, электронике, фотоискусстве, но основная область применения — математика. Рассмотрим, что это такое, как применяется и какие операции позволяет осуществить.

Что такое матрицы в математике

Матрица в математике — это абстрактный объект, имеющий вид таблицы чисел или других математических величин. Чаще таблица прямоугольная, но встречаются и другие виды (квадратные, треугольные).

Обычно матрица называется заглавной буквой латинского алфавита: матрица A, матрица B. В таблице есть строки (их количество называется m) и столбцы (их количество называется n). Количество строк и столбцов определяет размер матрицы и может называться порядком. Матрицы такого типа называются матрицами строения m×n, или размера m×n, или порядка m×n.

Элементы матрицы, т. е. числа или остальные величины, называются строчной буквой. Они имеют 2 нижних индекса, необходимых для определения их положения в матрице. Например, элемент a13 располагается на пересечении 2 строки и 3 столбца. Значения элемента а13 читаются по-отдельности, не как целое число: «а один-три».

Откуда они взялись и чем полезны

Первые упоминания матрицы появились в Древнем Китае. Это была квадратная таблица, получившая название магического или волшебного квадрата. Самым древним и известным считается квадрат 3×3, датируемый около 2200 г до н.э. Он был высечен на панцире черепахи. В Китае его называют квадрат Ло Шу, а в Западной Европе — «Печать Сатурна».

 

Таким же древним является квадрат, найденный в Кхаджурахо, столице средневекового государства Чандела (IX–XIII вв. ) в Центральной Индии. Это первый из «дьявольских квадратов». Также он называется пандиагональным.

 

В древности матрицы были необходимы преимущественно для решения линейных уравнений. Когда матрицы появились в арабских странах, стали разрабатываться принципы работы с ними, в том числе, принцип сложения. В XVIII веке швейцарский математик, «отец линейной алгебры» Габриэль Крамер опубликовал правило Крамера. Это способ решения систем линейных уравнений с помощью матрицы.

Источник: ruspekh.ru

Способ Крамера не подходит для решения тех систем линейных уравнений, в которых может быть бесконечное множество решений.

В следующем веке появляется метод немецкого математика Карла Фридриха Гаусса. Этот способ решения алгебраических уравнений не является открытием ученого. Впервые о методе Гаусса написали в китайском трактате «Математика в девяти книгах», а сам он только привел способ в удобную форму.

Для решения уравнений таким способом необходимо записать расширенную матрицу системы.

Источник: ruspekh.ru

В отличие от метода Крамера, правило Гаусса можно использовать для решения любых систем линейных уравнений.

Детальная разработка теории матриц активно продолжилась с середины XIX века. Наиболее значимые ученые: Уильям Гамильтон, Артур Кэли, Карл Вейерштрасс, Мари Энмон Камиль Жордан, Фердинанд Георг Фробениус.

Сам термин «матрица» предложил английский математик Джеймс Сильвестр в 1850 г.

В наше время матрицы используются не только для записи и решения систем линейных уравнений. Списки, статистические данные, табеля с информацией — все это в какой-то степени матрица. Их применяют для упрощения подачи и работы с информацией в любой сфере. Например, таблица продаж, где указан год (первый столбец), вид продукции (первая строка), а остальные значения — количество проданных единиц.

Обозначения матриц

Помимо самого термина «матрицы», при их решении нужно знать и другие обозначения.

Элементы матрицы — любые математические объекты: числа, переменные, другие матрицы. Элемент обозначается как a

ab, где a — номер строки расположения элемента, b — номер столбца.

Главная диагональ матрицы — диагональ, пересекающая квадратную матрицу из верхнего левого угла в нижний правый угол (квадратные матрицы имеют одинаковое количество строк и столбцов). Прямоугольные матрицы также могут иметь диагонали: они пересекают элементы с одинаковыми индексами.

Побочная диагональ матрицы — диагональ, пересекающая верхний правый и нижний левый углы. Для прямоугольного вида матриц понятие «побочные диагонали» не используется.

Диагональные элементы — числа и другие математические величины матрицы, расположенные на главной диагонали.

Размер (порядок) матрицы — произведение количества строк на количество столбцов: m×n. Например, если матрица содержит 2 строки и 3 столбца, то ее обозначают матрицей 2×3.

След матрицы — сумма элементов матрицы, расположенных на главной диагонали.

Обозначается как Sp (А) или Tr (A), где A — название матрицы.

Равные матрицы — матрицы, у которых соответствующие элементы равны.

Виды матриц, какие бывают

В математике существует несколько видов матриц в зависимости от их размера.

1. Матрица–строка. Имеет размер 1×n, т.е. состоит из одной строки и нескольких столбцов.
   \(\begin{vmatrix}54&2&-7&0&4\end{vmatrix}\)
2. Матрица–столбец. Имеет размер m×1, т.е. состоит из одного столбца и нескольких строк.
   \(\begin{vmatrix}3\\-6\\64.5\end{vmatrix}\)

Также различают матрицы по значениям их элементов.

1. Нулевая матрица. Все элементы матрицы равны 0.
   \(\begin{vmatrix}0&0&0\\0&0&0\end{vmatrix}\)
2. Квадратная матрица. Количество строк и столбцов одинаковое: m=n.
   \(\begin{vmatrix}4&5&1\\5&0&0\\-2&2&-8\end{vmatrix}\)
3. Диагональная матрица — разновидность квадратной матрицы, у которой все элементы равны 0, за исключением диагональных элементов.
   \(\begin{vmatrix}3&0&0\\0&-8&0\\0&0&1.5\end{vmatrix}\)
4. Единичная матрица — разновидность диагональной матрицы. На главной диагонали расположены 1, а все остальные элементы равны 0. Обозначается латинской буквой E.
   \(\begin{vmatrix}1&0&0\\0&1&0\\0&0&1\end{vmatrix}\)
5. Треугольная матрица. Имеет 2 разновидности: верхняя и нижняя. У верхней треугольной матрицы равны 0 элементы под главной диагональю, а у нижней треугольной матрицы — над главной диагональю.
   
   \(A=\begin{vmatrix}4&1.5&-2\\0&1&7\\0&0&4\end{vmatrix}\)

Треугольная матрица всегда квадратная: m=n.

6. Противоположная матрица. Обозначается -A и всегда рассматривается в отношении матрицы A. Ее элементы имеют обратный знак от элементов матрицы A.
7. Кососимметрическая (антисимметричная) матрица. T=\begin{vmatrix}0&-5&-217\\5&0&43\\217&-43&0\end{vmatrix}\)

Кососимметрическая матрица всегда квадратная.

8. Симметрическая матрица. Элементы лежат симметрично по отношению к главной диагонали. Матрица всегда квадратная.
   \(A=\begin{vmatrix}1&3&0\\3&2&6\\0&6&5\end{vmatrix}\)
9. Трапециевидная матрица. Есть ряд условий, при которых матрица становится такого вида. Например, она должна быть квадратной или прямоугольной, при этом количество столбцов обязательно больше числа строк. Также элементы, расположенные над главной диагональю, не равны 0, а элементы под главной диагональю равны 0.
   
   \(A=\begin{vmatrix}1&2&3&4&5&6\\0&-1&0&7&-3&2\\0&0&4&1&-1&-2\end{vmatrix}\)

Применение матриц в математико-экономическом моделировании

С древности и по настоящее время матрицы используются для решения и удобной записи системы линейных алгебраических или дифференциальных уравнений. Но их также применяют в математико-экономическом моделировании для структурирования данных и комфортной работы с ними.

Наиболее популярной является матричная модель экономики «затраты–выпуск». Ее внедрил Василий Леонтьев — американский экономист. За развитие этого метода он получил нобелевскую премию: матричная модель упростила решение некоторых экономических проблем. В последствии Леонтьева стали называть «апостолом планирования».

Суть модели «затраты–выпуск» в том, что экономист разделил производственный сектор экономики на отрасли, число которых обозначается n. 1 отрасль — 1 вид продукции. Значит, n количество отраслей выпускает n количество продуктов. Это приводит к появлению межотраслевых связей: одна отрасль заимствует у другой продукт и использует в процессе производства своей продукции. Данная балансовая модель представлена в виде системы линейных уравнений, решаемых с помощью матрицы.

Какие операции можно производить с матрицами

С матрицами можно проводить несколько операций.

1. Сложение и вычитание. Это действие можно проводить только с теми матрицами, у которых одинаковый размер. Например, матрица размера 3×2. Ответом будет матрица такого же размера. Чтобы получить ответ нужно вычесть или сложить соответствующие элементы двух матриц. Т.е. при сложении элемент a ₁₁ складывается с элементом b₁₁.
2. Умножение матрицы на число. Каждый элемент матрицы нужно умножить на число. Получится матрица такого же размера.
3. Умножение матриц. Не все матрицы можно умножить между собой. Обязательное свойство: число столбцов первой матрицы должно равняться числу строк второй матрицы. Например, можно умножить матрицу A размером 3×2 и матрицу B размером 2×3. Как осуществляется умножение: чтобы получить элемент a₁₁ новой матрицы, нужно поочередно умножить элементы строки матрицы A на соответствующие элементы столбца матрицы B, а затем суммировать эти произведения.

При умножении матрицы нельзя менять местами.

4. Транспонирование матрицы. Смена мест строк и столбцов матрицы. Первая строка матрицы становится первым столбцом. Дальше по аналогии.

Примеры решения задач на матрицы

Пример решения задачи на умножение.

Дано: \( A=\begin{vmatrix}1&-1\\2&0\\3&0\end{vmatrix},\;B=\begin{vmatrix}1&1\\2&0\end{vmatrix}\)

Найти: \(A*B\)

Решение: 

Назовем искомую матрицу \(C\). Она будет иметь следующий вид:

\(C=\begin{vmatrix}c_{11}&c_{12}\\c_{21}&c_{22}\\c_{31}&c_{32}\end{vmatrix}\)

Найдем значение каждого элемента:

\(с_{11}=a_{11}*b_{11}+a_{12}*b_{21}=1*1+(-1)*2=-1\)
\(c_{12}=a_{11}*b_{12}+a_{12}*b_{22}=1*1+(-1)*0=1\)
\(c_{21}=a_{21}*b_{11}+a_{22}*b_{21}=2*1+0*2=2\)
\(c_{22}=a_{21}*b_{12}+a_{22}*b_{22}=2*1+0*0=2\)
\(c_{31}=a_{31}*b_{11}+a_{32}*b_{21}=3*1+0*2=3\)

\(c_{32}=a_{31}*b_{12}+a_{32}*b_{22}=3*1+0*0=3\)

Ответ: \(C=\begin{vmatrix}-1&1\\2&2\\3&3\end{vmatrix}\)

Пример решения задачи на умножение матрицы на число 5.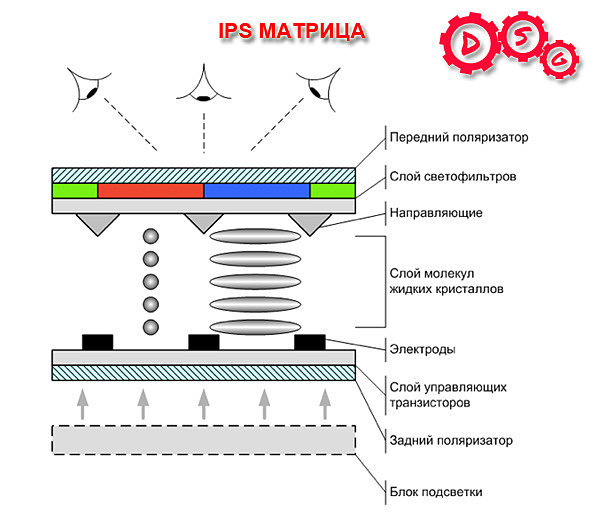

Дано: \(A=\begin{vmatrix}12&-1\\7&0\end{vmatrix}\)

Найти: \(A*5\)

Решение: \(5\ast\begin{vmatrix}12&-1\\7&0\end{vmatrix}=\begin{vmatrix}5\ast12&5\ast(-1)\\5\ast7&5\ast0\end{vmatrix}=\begin{vmatrix}60&-5\\35&0\end{vmatrix}\)

Ответ: \(\begin{vmatrix}60&-5\\35&0\end{vmatrix}\)

Учитесь работать с матрицами и продолжайте осваивать математику, а если задач накопилось слишком много и «горят» сроки, вам поможет сервис Феникс.Хелп. Обращайтесь!

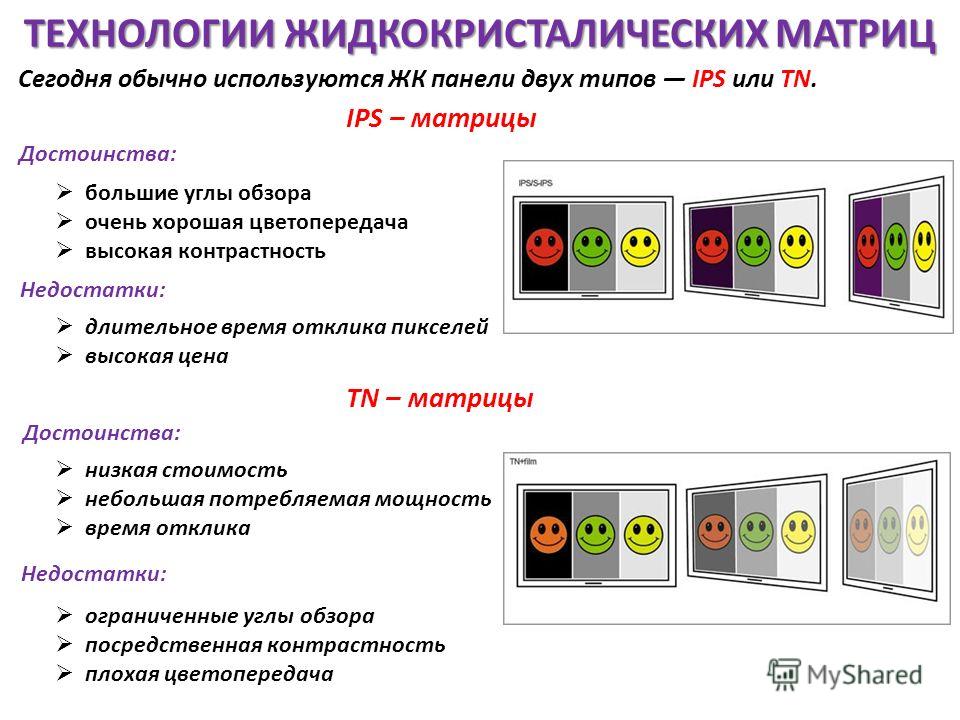
Типы матриц мониторов

Выбор монитора всегда сводится в первую очередь к выбору типа матрицы монитора. И когда вы уже определились, какого типа матрица вам нужна,  можно переходить к другим характеристикам монитора. В данной статье мы рассмотрим основные типы матриц мониторов, которые сейчас используются производителями.

 

Сейчас на рынке можно найти мониторы с такими типами матриц:

• TN+film (Twisted Nematic + film)
• IPS (SFT – Super Fine TFT)
• *VA (Vertical Alignment)
• PLS (Plane-to-Line Switching)

Рассмотрим все типы матриц мониторов по порядку

TN+film – самая простая и дешевая в производстве технология создания матриц. Благодаря своей низкой цене пользуется наибольшей популярностью. Еще несколько лет назад почти 100 процентов всех мониторов использовали эту технологию. И только продвинутые профессионалы, которым нужны качественные мониторы, покупали устройства, построенные на основе других технологий. Сейчас ситуация немного изменилась, мониторы подешевели и TN+film матрицы теряют свою популярность.

Преимущества и недостатки матриц TN+film:

• Низкая цена
• Хорошая скорость отклика
• Плохие углы обзора
• Низкая контрастность
• Плохая цветопередача

IPS – самый продвинутый тип матриц. Данная технология была разработана компаниями Hitachi и NEC. Разработчиками матрицы IPS удалось избавиться от недостатков TN+film, но в результате цена матриц такого типа значительно поднялась по сравнению с TN+film. Тем не менее, с каждым годом цены на мониторы с IPS снижаются и стают более доступными для обычного потребителя.

Преимущества и недостатки матриц IPS:

• Хорошая цветопередача
• Хорошая контрастность
• Широкие углы обзора
• Высока цена
• Большое время отклика

*VA это тип матриц мониторов, которые можно считать компромиссом между TN+film и IPS. Наибольшую популярность, среди таких матриц получила MVA (Multi-domain Vertical Alignment). Данная технология была разработана компанией Fujitsu.

Аналоги данной технологии,  разработанные другими производителями:

• PVA (Patterned Vertical Alignment) от Samsung.
• Super PVA от Sony-Samsung (S-LCD).
• Super MVA от CMO.

Преимущества и недостатки матриц MVA:

• Большие углы обзора
• Хорошая цветопередача (лучше, чем TN+film, но хуже чем IPS)
• Хорошая скорость отклика
• Глубокий черный цвет
• Не высокая цена
• Исчезновение деталей в тенях (по сравнению с IPS)

PLS – тип матриц, разработанный компанией Samsung как альтернатива дорогим IPS матрицам.

Преимущества и недостатки матриц PLS:

• Высокая яркость
• Хорошая цветопередача
• Широкие углы обзора
• Низкое потребление энергии
• Большое время отклика
• Низкая контрастность
• Неравномерная подсветка матрицы

 

Звоните или оставляйте заявку прямо на сайте! Наши специалисты с удовольствием помогут Вам

Здесь могла быть ваша реклама

Типы матриц — Примеры, Идентификация, Специальные матрицы

В линейной алгебре существует множество различных типов матриц. Все типы матриц различаются по элементам, порядку и определенному набору условий. Слово «матрицы» является формой множественного числа матрицы и реже используется для обозначения матриц.

В этой статье давайте узнаем о некоторых наиболее часто используемых типах матриц, их определениях и примерах.

1.	Какие бывают типы матриц?
2.	Определение типов матриц
3.	Другие типы матриц
4.	Специальные матрицы
5.	Часто задаваемые вопросы о типах матриц

Какие бывают типы матриц?

В этой статье описываются некоторые важные типы матриц, которые используются в математике, технике и естественных науках. Вот список наиболее часто используемых типов матриц в линейной алгебре:

• Матрица строк и матрица столбцов
• Прямоугольная матрица и квадратная матрица
• Идентификационная матрица
• Нулевая матрица
• Диагональная матрица
• Сингулярная матрица и невырожденная матрица
• Эрмитова матрица и косоэрмитова матрица
• Верхняя и нижняя треугольные матрицы
• Симметричная матрица и кососимметричная матрица
• Ортогональная матрица

Мы можем использовать эти различные типы матриц для организации данных по возрастным группам, лицам, компаниям, месяцам и т. д. Затем мы можем использовать эту информацию для принятия решений и решения многих математических задач.

Определение типов матриц

Матрицы бывают разных размеров, но обычно их форма остается неизменной. Размер матрицы называется ее порядком, который представляет собой общее количество строк и столбцов в данной матрице. На приведенном ниже изображении мы видим, как вычисляется размерность матрицы.

В этом разделе мы научимся определять типы матриц в зависимости от их размера:

Матрица строк и столбцов

Матрицы только с одной строкой и любым количеством столбцов известны как матрицы-строки и матрицы с одним столбцом и любое количество строк называется матрицей-столбцом. Давайте рассмотрим два примера ниже:

Матрица строк	Матрица столбцов
\(A=\left[\begin{array}{ll} 1 и 0 и 2 и 4\\ \конец{массив}\справа]\)	\(B=\left[\begin{массив}{c} 3\ 2\ 5 \конец{массив}\справа]\)
Имеется только одна строка, поэтому A — матрица-строка.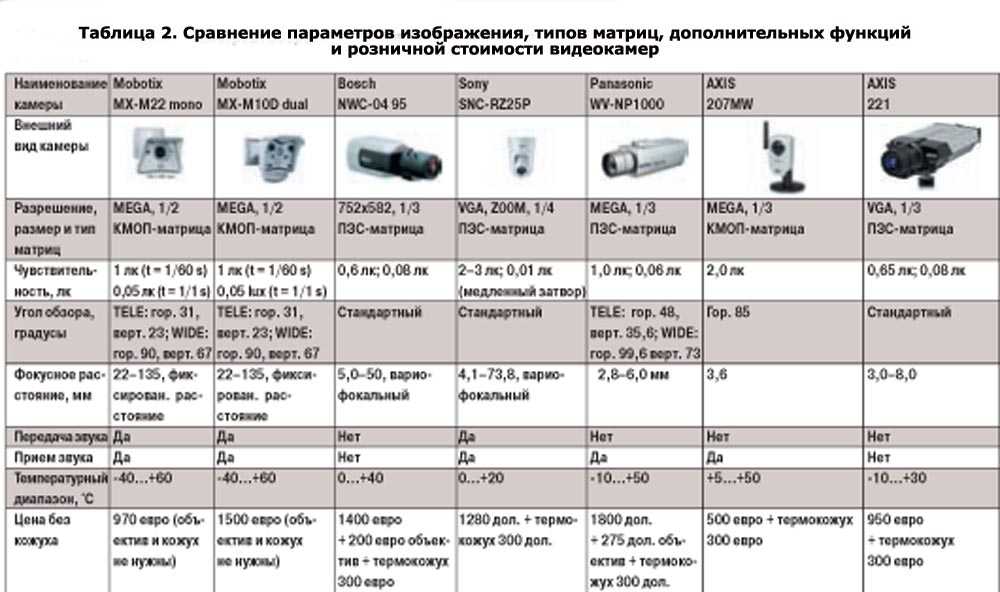	Имеется только один столбец, поэтому B является матрицей-столбцом.

Прямоугольная и квадратная матрица

Любая матрица, которая не имеет одинакового количества строк и столбцов, называется прямоугольной матрицей, а прямоугольная матрица может быть обозначена как B _{m × n} . Любая матрица, имеющая одинаковое количество строк и столбцов, называется квадратной матрицей, а квадратную матрицу можно обозначить как B _{n × n} . Давайте посмотрим на примеры ниже:

Прямоугольная матрица	Квадратная матрица
\(B = \left[\begin{array}{ccc} 2&-1&3&5\ 0 и 5 и 2 и 7\\ 1 и -1 и -2 и 9 \конец{массив}\справа] \)	\(C = \left[\begin{массив}{ccc} 2&-1&3\ 0 и 5 и 2 \ 1 и -1 и -2 \конец{массив}\справа] \)
В этой матрице три строки и четыре столбца, поэтому B — прямоугольная матрица.	В этой матрице три строки и три столбца, поэтому C — квадратная матрица.

Единичная и нулевая матрицы

Давайте посмотрим на единичную матрицу и нулевую матрицу.

Матрица идентичности	Нулевая матрица
Единичная матрица представляет собой квадратную диагональную матрицу, в которой все элементы на главной диагонали равны 1, а остальные элементы равны 0. Она обозначается I.	Любая матрица, в которой все элементы равны 0, называется нулевой матрицей.
\(I = \left[\begin{array}{ccc} 1&0&0\ 0&1&0\ 0 и 0 и 1 \конец{массив}\справа] \)	\(D = \left[\begin{массив}{ccc} 0&0&0\ 0&0&0\ 0 и 0 и 0 \end{массив}\right] \)

Другие типы матриц

Помимо наиболее часто используемых матриц, существуют и другие типы матриц, которые используются в высшей математике и компьютерных технологиях. Ниже приведены некоторые другие типы матриц:

Сингулярная и невырожденная матрица

Любая квадратная матрица, определитель которой равен 0, называется вырожденной матрицей, а любая матрица, определитель которой не равен 0, называется невырожденной матрицей. матрица. Определитель матрицы можно найти по формуле определителя. Давайте рассмотрим два примера ниже:

Сингулярная матрица	Несингулярная матрица
C = \(\left[\begin{array}{ccc} 1&1&1\ 1&1&1\ 1 и 1 и 1 \конец{массив}\справа] \)	D = \(\left[\begin{массив}{ccc} 2&1&1\ 1&2&1\ 1 и 1 и 1 \end{массив}\right] \)
|С| = \(\begin{vmatrix} 1&1&1\ 1&1&1\ 1 и 1 и 1 \end{vmatrix}\)	|Д| = \(\left|\begin{массив}{ccc} 2&1&1\ 1&2&1\ 1 и 1 и 1 \конец{массив}\право| \)
=1×(1×1-1×1)-1×(1×1-1×1)+1×(1×1-1×1) =1×(1-1)-1×(1-1)+1×(1-1) =1×(0)-1×(0)+1×(0) =0+0+0 =0	=2×(2×1-1×1)-1×(1×1-1×1)+1×(1×1-2×1) =2×(2-1)-1×(1-1)+1×(1-2) =2×(1)-1×(0)+1×(-1) =2-0-1 =1
Здесь |С| = 0, поэтому C — сингулярная матрица	Здесь |D| ≠ 0, поэтому D — неособая матрица

Диагональная матрица

Квадратная матрица, в которой все элементы равны 0, кроме тех элементов, которые находятся на диагонали, называется диагональной матрицей. Давайте рассмотрим примеры различных видов диагональных матриц: Скалярная матрица — это особый тип квадратной диагональной матрицы, в которой все диагональные элементы равны.

Диагональная матрица	Скалярная матрица
B = \(\left[\begin{массив}{llll} 1&0&0&0\ 0&5&0&0\ 0&0&2&0\ 0 и 0 и 0 и 4 \конец{массив}\справа]\)	C = \(\left[\begin{массив}{lll} 3&0&0\ 0 & 3 & 0 \ 0 и 0 и 3 \конец{массив}\справа]\)
Здесь мы видим, что кроме диагональных элементов все остальные элементы равны нулю. Следовательно, B — диагональная матрица.	Здесь мы видим, что диагональные элементы равны, а все остальные элементы равны нулю. Следовательно, C — скалярная матрица.

Верхняя и нижняя треугольная матрица

Верхняя треугольная матрица представляет собой квадратную матрицу, в которой все элементы, расположенные ниже диагональных элементов, равны 0. Нижняя треугольная матрица представляет собой квадратную матрицу, в которой все элементы находятся над диагональными элементами. диагональные элементы равны 0. Давайте посмотрим на примеры ниже:

Верхняя треугольная матрица	Нижняя треугольная матрица
B = \(\left[\begin{array}{lll} 3&2&1\ 0 и 4 и 5 \ 0 и 0 и 6 \конец{массив}\справа]\)	C = \(\left[\begin{массив}{lll} 3&0&0\ 4 & 1 & 0 \ 2 и 7 и 9 \конец{массив}\справа]\)
Здесь мы видим, что все элементы, находящиеся ниже главной диагонали, равны 0. Следовательно, B — верхнетреугольная матрица.	Здесь мы видим, что все элементы, находящиеся выше главной диагонали, равны 0. Следовательно, B — верхнетреугольная матрица.

Симметричная и кососимметричная матрица

Квадратная матрица D размера n×n считается симметричной тогда и только тогда, когда D ^T = D. Квадратная матрица F размера n×n считается кососимметричной тогда и только тогда, когда F ^T = — F. Рассмотрим примеры двух матриц D и F:

Симметричная матрица	Кососимметричная матрица
D = \(\left[\begin{массив}{lll} 2 и 3 и 6 \ 3 и 4 и 5 \ 6 и 5 и 9 \end{массив}\right] \) D T = \(\left[\begin{array}{lll} 2 и 3 и 6 \ 3 и 4 и 5 \ 6 и 5 и 9 \конец{массив}\справа]\)	F = \(\left[\begin{массив}{cc} 0 и 3 \ -3 и 0 \конец{массив}\справа]\) F T = \(\left[\begin{массив}{cc} 0&-3\ 3 и 0 \конец{массив}\справа]\) -F = \(\left[\begin{массив}{cc} 0&-3\ 3 и 0 \конец{массив}\справа]\)
Здесь D = D T . Следовательно, D — симметричная матрица.	Здесь, F T = -F. Следовательно, F — кососимметричная матрица.

Эрмитовы и косоэрмитовы матрицы

Существует небольшая разница между симметричными и эрмитовыми матрицами.

• Матрица называется эрмитовой, если и только она равна транспонированию сопряженной матрицы.
  Пример: \(\left[\begin{массив}{cc}
  3&3-2 я\\\
  3+2 я и 2
  \конец{массив}\справа]\)
• Матрица называется косоэрмитовой тогда и только тогда, когда она равна отрицательному значению сопряженной матрицы.
  Пример: \(\left[\begin{массив}{cc}
  3 я и 1+я \\
  -1+я и -я
  \конец{массив}\справа]\)

Булева матрица

Матрица считается булевой матрицей, если все ее элементы равны единицам или нулям. Давайте рассмотрим пример матрицы B, чтобы лучше понять это:

B = \(\left[\begin{array}{lll}
0&1&0\
1&0&1\
0 и 1 и 1
\end{array}\right]\)

Стохастические матрицы

Стохастическая матрица — это тип матрицы, все элементы которой представляют вероятность. Квадратная матрица C считается левостохастической, если все ее элементы неотрицательны, а сумма элементов в каждом столбце равна 1. Точно так же матрица, все элементы которой являются неотрицательными, так что элементы в каждой строке в сумме составляют 1 называется правой стохастической матрицей. Рассмотрим пример левой стохастической матрицы C здесь:

C = \(\left[\begin{массив}{lll}
0,3&0,4&0,5\
0,3&0,4&0,3\
0,4 и 0,2 и 0,2
\end{array}\right]\)

Ортогональная матрица

Квадратная матрица B считается ортогональной матрицей, когда B × B ^T = I, где I — единичная матрица, а B ^T — транспонирование матрицы B. Возьмем пример матрицы B:

B =\(\left[\begin{array}{ll} 0 & 1 \\\ 1 и 0 \конец{массив}\справа]\)	B T =\(\left[\begin{array}{ll} 0 & 1 \\\ 1 и 0 \конец{массив}\справа]\)
B × B T = \(\left[\begin{array}{ll} 0 & 1 \\\ 1 и 0 \end{массив}\right] \times\left[\begin{массив}{ll} 0 и 1 \\\ 1 и 0 \конец{массив}\справа]\) = \(\left[\begin{массив}{ll} 0+1 и 0+0 \\ \\ 0+0 и 1+0 \конец{массив}\справа]\) = \(\left[\begin{массив}{ll} 1 & 0 \\\ 0 и 1 \конец{массив}\справа]\) Здесь мы видим, что B × B T = I. Следовательно, B — ортогональная матрица.

Специальные матрицы

Помимо того, что мы узнали до сих пор, существуют некоторые специальные типы матриц:

Идемпотентная матрица

Квадратная матрица A называется идемпотентной матрицей тогда и только тогда, когда A ⁿ = A, для каждого n ≥ 2. Например, А ² = А, А ³ = А и так далее. Чтобы проверить, является ли квадратная матрица A идемпотентной, достаточно проверить, является ли A ² = A.

Нильпотентная матрица

Квадратная матрица A порядка n нильпотентна тогда и только тогда, когда A ^k = O для некоторого k ≤ n. Например, A = \(\left[\begin{array}{ll}
2&-4\\
1 и -2
\end{array}\right]\) является нильпотентной матрицей, поскольку A ² = O, где O является нулевой матрицей порядка 2.

Инволютивная матрица

Квадратная матрица A называется инволютивной матрицей тогда и только тогда, когда A ^-1 = A. Например, единичная матрица является инволютивной, поскольку она равна своей обратной.

Важные примечания о типах матриц:

• Матрицы только с одной строкой и любым количеством столбцов называются матрицами-строками.
• Матрицы с одним столбцом и любым количеством строк называются матрицами-столбцами.
• Постоянные матрицы — это матрицы, в которых все элементы являются константами для любой заданной размерности/порядка матрицы.

☛ Статьи по теме:

• Матричный калькулятор
• Формула матрицы
• Калькулятор диагональной матрицы
• Калькулятор матрицы транспонирования

Часто задаваемые вопросы о типах матриц

Назовите различные типы матриц.

Матрицы делятся на несколько типов в зависимости от их порядка, элементов и некоторых других условий. Вот список различных типов матриц :

• Матрица строк
• Матрица столбца
• Сингулярная матрица
• Несингулярная матрица
• Прямоугольная матрица
• Квадратная матрица
• Идентификационная матрица
• Матрица единиц
• Нулевая матрица
• Диагональная матрица
• Верхняя матрица
• Нижняя треугольная матрица
• Ортогональная матрица
• Симметричная матрица
• Кососимметричная матрица
• Эрмитова матрица
• Косоэрмитова матрица

Как определить типы матриц?

Одним из способов определения типа матрицы является проверка ее размерности. Размерность матрицы — это общее количество строк и столбцов в данной матрице. Рассмотрим пример матрицы B = [ 1 2 5 7 0]. В этой матрице одна строка и 5 столбцов, следовательно, ее размерность равна 1 × 5. Если матрица имеет одну строку и много столбцов, то ее можно рассматривать как матрицу-строку, и, следовательно, матрица B является матрицей-строкой. .

Какой тип матрицы 2×2?

Квадратная матрица — это матрица размерности n × n, т. е. имеющая одинаковое количество строк и столбцов. Матрица типа 2 × 2 имеет 2 строки и 2 столбца, поэтому ее можно рассматривать как квадратную матрицу.

Матрица какого типа необратима?

Квадратная матрица называется обратимой тогда и только тогда, когда ее определитель не равен нулю. Например, матрица 2 x 2 обратима только в том случае, если определитель этой матрицы не равен 0. Если определитель этой матрицы равен 0, то матрица необратима и не может иметь реверса. Таким образом, любая сингулярная матрица, определитель которой равен нулю, никогда не будет обратимой.

Какие типы матриц имеют обратные?

Матрицы, определитель которых не равен нулю, могут иметь обратные. Несингулярная матрица — это тип матрицы, определитель которой не равен нулю, и, следовательно, мы можем найти обратную для невырожденной матрицы.

(a b c) Какой тип матрицы?

(a b c) — это матрица с одной строкой и тремя столбцами, и этот тип матрицы с одной строкой и многими столбцами называется матрицей-строкой. Таким образом, (ABC) — матрица-строка.

Что такое треугольная матрица и ее виды?

Треугольная матрица считается особым типом квадратной матрицы, в которой либо все элементы выше диагональных элементов, либо все элементы ниже диагональных элементов равны нулю. Два типа треугольной матрицы — это верхняя треугольная матрица и нижняя треугольная матрица. Верхняя треугольная матрица — это квадратная матрица, в которой все элементы, расположенные ниже диагональных элементов, равны 0. Нижняя треугольная матрица — это квадратная матрица, в которой все элементы, находящиеся выше диагональных элементов, равны 0,9. 0003

Матрица какого типа называется нулевой матрицей?

Нулевая матрица — это тип матрицы, который называется нулевой матрицей, поскольку все элементы в нулевой матрице равны нулю. У нее нет обратной, так как ее определитель равен 0, и, следовательно, это сингулярная матрица.

Свойства с примерами и специальными матрицами

Матрицы — форма множественного числа матрицы, которая символизирует прямоугольный массив или таблицу, в которой числа/элементы организованы в строки и столбцы. Матрицы могут содержать любое количество столбцов и строк. Прямоугольный массив из m × n чисел (действительных или комплексных) в кадре из m горизонтальных линий (обозначается как 9).0045 строк ) и n вертикальных линий (названных как столбцов ), называется матрицей, имеющей порядка m на n, и записывается как матрица m × n, как показано ниже.

\(A=\left[\begin{matrix}a_{11}&a_{12}&……&a_{1n}\\a_{21}&a_{22}&……&a_{2n}\\ . & .&.&.\\ .&.&.&.\\a_{m1}&a_{m2}&……&a_{mn}\end{matrix}\right] \)

\(\text{Здесь числа }a_{11},a_{12\ },\dots..\ \text{etc известны как элементы матрицы A} \)

Пример матрицы:

\(B=\begin{bmatrix}2&3&6\\3&4&5\\6&5&9\end{bmatrix}_{3\times3} \)

Приведенная выше матрица B имеет порядок 3 × 3. Следовательно, всего в матрице 9 элементов. Здесь горизонтальный массив идентифицируется как строки, а вертикальный массив распознается как столбцы.

Матрицы доступны во всех размерах, но их форма обычно остается неизменной. Размер матрицы называется ее размерностью, которая представляет собой общее количество строк и столбцов в назначенной матрице. Над матрицами могут выполняться различные операции, такие как сложение матриц, вычитание матриц, скалярное умножение матриц, умножение матриц, транспонирование матриц и т. д. Существуют различные типы матриц в зависимости от количества компонентов и организации элементов в матрицах.

В линейной алгебре существует множество типов матриц. Все типы матриц различаются по компонентам, порядку и определенному набору условий. Различные типы матриц: матрица-строка, матрица-столбец, одноэлементная матрица, прямоугольная матрица, квадратная матрица, единичная матрица, нулевая матрица, диагональная матрица и т. д. Существуют также некоторые специальные матрицы.

Какие бывают типы матриц?

В линейной алгебре существуют различные типы матриц. Все типы матриц различаются по компонентам, порядку и определенному набору условий. Различные типы матриц с примерами приведены ниже:

1. Матрица-строка: Любая матрица, состоящая из одной строки и n столбцов, называется матрицей-строкой.

т.е. \(A=\left[a_{11}\dots..a_{1n}\right]_{1\times n} \)

Пример матрицы строк:

\(P=\begin{bmatrix }\ 1&-3&17\end{bmatrix} \)

2. Матрица-столбец: Любая матрица, имеющая m строк и один столбец, называется матрицей-столбцом.

т.е. \(A=\begin{bmatrix}a_{11}\\\vdots\\a_{m1}\end{bmatrix}_{m\times1}\)

Пример матрицы столбцов:

\(Q=\begin{bmatrix}2\\3\\7\end{bmatrix}\)

3. Нулевая матрица или нулевая матрица: Любая матрица, в которой все компоненты равны нулю, называется нулевой матрицей. Она также распознается как нулевая матрица и обозначается O. нулевая матрица порядка 3 x 3.

4. Одноэлементная матрица: Любая матрица называется одноэлементной, если матрица имеет только один элемент.

т. е. \(A=\left[a_{ij}\right]_{ m\times n}\) является одноэлементной матрицей, если m = n = 1.

Пример одноэлементной матрицы:

\(\left [4\right],\left[7\right],\left[b\right]\) являются примерами одноэлементной матрицы.

5. Квадратная матрица: Любая матрица, в которой количество строк равно количеству столбцов, скажем «A», называется квадратной матрицей порядка n.

т. е. \(A=\left[a_{ij}\right]_{ m\times n}\) объявляется квадратной матрицей порядка n, если m = n.

Пример квадратной матрицы:

\(B=\begin{bmatrix}2&3&6\\3&4&5\\6&5&9\end{bmatrix}\)

6. Прямоугольная матрица:  Матрица идентифицируется как прямоугольная, если количество строк не совпадает с количеством столбцов.

Пример прямоугольной матрицы:

\(B=\begin{bmatrix}2&3&6&-1\\3&4&5&5\\6&5&9&-1\end{bmatrix}\)

Здесь мы видим, что есть четыре столбца и три строки в эта матрица, поэтому B является прямоугольной матрицей.

7. Горизонтальная матрица:  Матрица порядка m x n называется горизонтальной матрицей, если n > m. То есть, если количество столбцов больше, чем количество строк в горизонтальной матрице.

\(B=\begin{bmatrix}1&2&3&4\\4&3&2&1\end{bmatrix}\)

8. Вертикальная матрица:  Матрица порядка m x n называется вертикальной, если m > n. То есть, если количество строк больше, чем количество столбцов в вертикальной матрице.

\(B=\begin{bmatrix}1&1\\2&5\\3&6\\2&4\end{bmatrix}\)

9. Диагональная матрица:  Любая квадратная матрица, в которой все компоненты равны нулю, за исключением компонентов в главная диагональ называется диагональной матрицей.

То есть \(A=\left[a_{ij}\right]_{n\times n}\) является диагональной матрицей, если \(a_{ij}=0\) для i не равно j.

Пример диагональной матрицы:

\(B=\begin{bmatrix}2&\ 0&\ \ 0\\0&\ 1&\ \ 0\\0&\ 0&-2\end{bmatrix}_{3\times3}\ )

\(P=\begin{bmatrix}1&0&0&0\\0&5&0&0\\0&\ 0&2&0\\0&0&0&4\end{bmatrix}\)

Здесь мы можем понять, что кроме диагональных элементов все остальные элементы равны до нуля. Следовательно, вышеупомянутый тип матрицы в математике является диагональной матрицей.

10. Прямоугольные диагональные матрицы: Прямоугольная диагональная матрица — это тип матрицы, которая также имеет одну ведущую диагональ с числами, а остальные записи — нули. Ведущая диагональ выбирается из самого большого квадрата в неквадратной матрице.

\(\begin{bmatrix}1&0&0&0&0\\0&4&0&0&0\\0&0&7&0&0\end{bmatrix}\)

11. Скалярная матрица: Диагональная матрица, в которой все главные диагональные компоненты равны, называется скалярной матрицей.

Пример скалярной матрицы:

\(B=\begin{bmatrix}2&\ 0&\ 0\\0&\ 2&\ 0\\0&\ 0&\ 2\end{bmatrix}_{3\times3}\)

\(B=\begin{bmatrix}-5&\ 0&\ 0\\0&\ -5&\ 0\\0&\ 0&-5\end{bmatrix}_{3\times3}\)

12. Единичная матрица или единичная матрица: Диагональная матрица, в которой все главные диагональные компоненты равны 1, называется единичной матрицей. Она также признается единичной матрицей. Единичная матрица порядка n обозначается I или \(I_{n}\).

Примеры матрицы идентичности:

\(I_2=\begin{bmatrix}1&\ \ 0\\0&\ \ 1\end{bmatrix}\)

\(B=\begin{bmatrix}1&0&0\\0&1&0\ \0&0&1\end{bmatrix}_{3\times3}\)

Подробнее об определителях

Специальные типы матриц

Существуют специальные типы матриц, которые применяются в передовых математических расчетах и ​​компьютерных технологиях:

1. Вырожденные и невырожденные матрицы: Любая квадратная матрица, определитель которой равен нулю называется сингулярной матрицей, а любая матрица, определитель которой не равен нулю, называется невырожденной матрицей.

Пример сингулярной матрицы:

\(B=\begin{bmatrix}1&\ 1&1\\1&1&1\\1&1&1\end{bmatrix}\left|B\right|=\begin{vmatrix}1&1&1\\1&1&1\\ 1&1&1\конец{vmatrix}=1\влево(1-1\вправо)-1\влево(1-1\вправо)+1\влево(1-1\вправо)\влево|B\вправо|=0+0 +0=0\)

Пример невырожденной матрицы:

\(B=\begin{bmatrix}2&\ 1&1\\1&2&1\\1&1&1\end{bmatrix}\left|B\right|=\begin{vmatrix}2&1&1\\1&2&1 \\1&1&1\end{vmatrix}=2\влево(2-1\вправо)-1\влево(1-1\вправо)+1\влево(1-2\вправо)\влево|B\вправо|=2 -0-1=1\)

Любая квадратная матрица называется треугольной матрицей , если элементы выше или ниже главной диагонали равны нулю. Существует 2 типа треугольных матриц, как показано ниже:

2. Верхнетреугольная матрица: Любая квадратная матрица \(A=\left[a_{ij}\right]_{n\times n}\) называется верхнетреугольной матрицей, если \(a_{ij} =0\) ∀ i > j.

Пример верхней треугольной матрицы:

\(B=\begin{bmatrix}2&\ 3&\ \ 4\\0&\ 1&\ \ 5\\0&\ 0&-2\end{bmatrix}_{3\times3} \)

3. Нижняя треугольная матрица: Любая квадратная матрица, скажем, \(A=\left[a_{ij}\right]_{n\times n}\) называется нижней треугольной матрицей, если \(a_{ ij}=0\) ∀ i < j. 9{’} (транспонировать A) \)тогда A называется кососимметричной матрицей.

Пример кососимметричной матрицы:

\(Q=\begin{bmatrix}\ 0&\ \ 3\\-3&\ \ 0\end{bmatrix}\)

Характеристики симметричных и кососимметричных матриц

• Для кососимметричной матрицы A все ее диагональные элементы равны нулю. то есть \(a_{ii\left(i=j\right)}=0\) ∀ i и j.
• Нулевая матрица / Нулевая матрица является как симметричной, так и кососимметричной матрицей.
• A+B и AB также являются симметричными матрицами. 9{\ тета} \).

  \(Q=\begin{bmatrix}0&\ -2+i\\2-i&\ \ \ \ \ 0\end{bmatrix}\)

  Подробнее о матрице преобразования

  Типы матриц в табличной форме

  The types of matrices with examples are given in the tabular form below:

  Type of Matrices	Matrix Representation Details	Matrix Example
  Row Matrix	\(A=\left[a_{ij}\right]_{1\times n}\)	\(P=\begin{bmatrix}\ 1&-3&17\end{bmatrix}\)
  Столбец Матрица	\(A=\left[a_{ij}\right]_{m\times1}\)	\(Q=\begin{bmatrix}2\\3\\7\end{bmatrix}\)
  Нулевая или нулевая матрица	\(A=\left[a_{ij}\right]_{m\times n}\text{, где }a_{ij}=0\)	\(B= \begin{bmatrix}0&0&0\0&0&0\0&0&0\end{bmatrix}_{3\times3}\)
  Одноэлементная матрица	\(A=\left[a_{ij}\right]_{m\times n}\text{где }m=n=1\)	\(\left[4\right],\left[ 7\right],\left[b\right]\)
  Горизонтальная матрица	\(A=\left[a_{ij}\right]_{m\times n}\text{где }n\ gt m\)	\(B=\begin{bmatrix}1&2&3&4\\4&3&2&1\end{bmatrix}\)
  Вертикальная матрица	\(A=\left[a_{ij}\right]_{ m\times n}\text{ где}m>n\)	\(B=\begin{bmatrix}1&1\\2&5\\3&6\\2&4\end{bmatrix}\)
  Квадратная матрица	\(A=\left[a_{ij}\right]_{m\times n}\text{где}m=n\)	\(B=\begin{bmatrix} 2&3&6\\3&4&5\\6&5&9\end{bmatrix}\)
  Диагональная матрица	\(A=\left[a_{ij}\right]_{n\times n}\text{ где } a_{ ij}=0\text{ for } i\ne j\)	\(P=\begin{bmatrix}1&0&0&0\\0&5&0&0\\0&\ 0&2&0\\0&0&0&4\end{bmatrix}\)
  Скаляр Матрица	\(A=\left[a_{ij}\right]_{n\times n}\text{, где }a_{ij}=\begin{Bmatrix}0&i\ne j\\k&i=j\end{ Bmatrix}\) Здесь k — константа.	\(B=\begin{bmatrix}-5&\ 0&\ 0\\0&\ -5&\ 0\\0&\ 0&-5\end{bmatrix}_{3\times3}\)
  Идентичность или единичная матрица	\(A=\left[a_{ij}\right]_{n\times n}\text{, где }a_{ij}=\begin{Bmatrix}0&i\ne j\\1&i= j\end{Bmatrix}\)	\(B=\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}_{3\times3}\)
  Равная матрица	\(A=\left[a_{ij}\right]_{m\times n}\text{ и }B=\left[b_{ij}\right]_{r\ раз s}\text{, где }a_{ij}=b_{ij},\m=r,\text{и} n=s\)	\(A=\begin{bmatrix}2&-5\\2& \ 4\end{bmatrix},\ B=\begin{bmatrix}2&-5\\2&\ 4\end{bmatrix}\) Здесь A и B — равные матрицы.
  Верхняя треугольная матрица	\(A=\left[a_{ij}\right]_{n\times n}\text{ for }a_{ij}=0\ ∀\ i>j\)	\(B=\begin{bmatrix}2&\ 3&\ \ 4\\0&\ 1&\ \ 5\\0&\ 0&-2\end{bmatrix}_{3\times3}\)
  Нижняя треугольная матрица	\(A=\left[a_{ij}\right]_{n\times n}\text{ for }a_{ij}=0\ ∀\ i	\(B=\begin{bmatrix}2&\ 0&\ \ 0\\3&\ 1&\ \ 0\\4&\ 5&-2\end{bmatrix}_{3\times3}\)
  Сингулярная матрица	\(\left|A\right|=0\)	\(B=\begin{bmatrix}1&\ 1&1\\1&1&1\\1&1&1\end{bmatrix}\)
  Несингулярная матрица	\(\влево|А\вправо|\ne 0\)	\(B=\begin{bmatrix}2&\ 1&1\\1&2&1\\1&1&1\end{bmatrix}\)
  Симметричные матрицы	\(A=\left[a_{ij}\right]\ text{ где }a_{ij}=a_{ij}\) То есть A=A’ .	\(B=\begin{bmatrix}\ \ 1&4&-3\\\ \ 4&1&\ 7\\3&7&\ 0\end{bmatrix}\)
  Кососимметричные матрицы	\(A= \left[a_{ij}\right]\text{ где }a_{ij}=-a_{ij}\) То есть A=-A’.	\(Q=\begin{bmatrix}\ 0&\ \ 3\\-3&\ \ 0\end{bmatrix}\) 9{m} = O\), где O — нулевая матрица порядка n.	–

  Важные сведения о типах матриц
  • Для матричных продуктов матрицы должны быть совместимы. Это утверждает, что две матрицы A и B совместимы, если количество столбцов в A= количеству строк в B.
  • Если мы умножаем матрицу на скалярное значение, то это распознается как скалярное умножение.
  • Чтобы матрица была симметричной, она должна быть квадратной, т. е. иметь одинаковое количество строк и столбцов.
  • Если m=n, матрица считается квадратной.
  • Если m \ne n, матрица считается прямоугольной.
  • Здесь m обозначает количество строк, а n обозначает количество столбцов.
  • Диагональная матрица, в которой все главные диагональные компоненты равны 1, называется единичной матрицей. Она также распознается как единичная матрица, тогда как единичная матрица порядка n обозначается \(I\) или \(I_n\).
  • Единичная матрица, нулевая матрица или нулевая матрица, а также скалярная матрица являются примерами диагональной матрицы, поскольку во всех них неглавным диагональным элементам присваивается нуль.

  Мы надеемся, что приведенная выше статья о типах матриц поможет вам понять и подготовиться к экзамену. Оставайтесь с нами в приложении Testbook, чтобы получать больше обновлений по связанным с математикой темам и другим подобным предметам. Кроме того, обратитесь к серии тестов, доступных для проверки ваших знаний по нескольким экзаменам.

  Часто задаваемые вопросы о типах матриц

  В.1 Какие существуют типы матриц?

  Ответ 1 Существуют различные типы матриц: матрица-строка, матрица-столбец, одноэлементная матрица, прямоугольная матрица, квадратная матрица, единичная матрица, нулевая матрица, диагональная матрица и т. д.

  В.2 Можно ли добавлять матрицы разных размеров?

  Ответ 2 Для выполнения сложения или вычитания матриц они должны иметь одинаковый размер или размерность. Если сложение или разность двух матриц, имеющих разные размеры или размерности, не определены.

  Q.3 Каков порядок матрицы?

  Ответ 3 Говорят, что матрица с m строк и n столбцов имеет порядок m x n.

  Q.4 Что такое транспонирование матрицы?

  Ответ 4 Можно определить транспонирование матрицы путем переключения строк в столбцы и столбцов в строки для заданной матрицы, т. е. строки и столбцы меняются местами.

  В.5 Что такое матрицы?

  Ответ 5 Матрицы — форма множественного числа матрицы, которая символизирует прямоугольный массив или таблицу, в которой числа/элементы организованы в строки и столбцы. Матрицы могут содержать любое количество столбцов и строк.