Криптосистема с открытым ключом | Контроль Разума

Криптографическая система с открытым ключом (или Асимметричное шифрование, Асимметричный шифр) — система шифрования и/или электронной цифровой подписи (ЭЦП), при которой открытый ключ передаётся по открытому (то есть незащищённому, доступному для наблюдения) каналу, и используется для проверки ЭЦП и для шифрования сообщения. Для генерации ЭЦП и для расшифрования сообщения используется секретный ключ. ^[1]Криптографические системы с открытым ключом в настоящее время широко применяются в различных сетевых протоколах, в частности, в протоколах TLS и его предшественнике SSL (лежащих в основе HTTPS), в SSH. Также используется в PGP, S/MIME.

Идея криптосистемы с открытым ключом Править

Идея криптографии с открытым ключом очень тесно связана с идеей односторонних функций, то есть таких функций $ f(x) $, что

x	легко вычислимо	$ f(x) $
	——————————→
	←···································
	сложновычислимо

По известному $ x $ довольно просто найти значение $ f(x) $, тогда как определение $ x $ из $ f(x) $ сложно в смысле теории.

Но сама односторонняя функция бесполезна в применении: ею можно зашифровать сообщение, но расшифровать нельзя. Поэтому криптография с открытым ключом использует односторонние функции с лазейкой. Лазейка — это некий секрет, который помогает расшифровать. То есть существует такой $ y $, что зная $ f(x) $, можно вычислить $ x $. К примеру, если разобрать часы на множество составных частей, то очень сложно собрать вновь работающие часы. Но если есть инструкция по сборке (лазейка), то можно легко решить эту проблему.

Понять идеи и методы криптографии с открытым ключом помогает следующий пример — хранение паролей в компьютере. Каждый пользователь в сети имеет свой пароль. При входе, он указывает имя и вводит секретный пароль. Но если хранить пароль на диске компьютера, то кто-нибудь его может считать (особенно легко это сделать администратору этого компьютера) и получить доступ к секретной информации. Для решения задачи используется односторонняя функция. При создании секретного пароля в компьютере сохраняется не сам пароль, а результат вычисления функции от этого пароля и имени пользователя. Например, пользователь Алиса придумала пароль «Гладиолус». При сохранении этих данных вычисляется результат функции $ f $

(АЛИСАГЛАДИОЛУС), пусть результатом будет строка РОМАШКА, которая и будет сохранена в системе. В результате файл паролей примет следующий вид:

Имя	$ f $(имя_пароль)
АЛИСА	РОМАШКА
БОБ	НАРЦИСС

Вход в систему теперь выглядит так:

Имя:	АЛИСА
Пароль:	ГЛАДИОЛУС

Когда Алиса вводит «секретный» пароль, компьютер проверяет, даёт или нет функция, применяемая к

АЛИСАГЛАДИОЛУС, правильный результат РОМАШКА, хранящийся на диске компьютера. Стоит изменить хотя бы одну букву в имени или в пароле, и результат функции будет совершенно другим. «Секретный» пароль не хранится в компьютере ни в каком виде. Файл паролей может быть теперь просмотрен другими пользователями без потери секретности, так как функция необратимая.

Полезно рассмотреть также схему на примере большого абонентского справочника, состоящего из нескольких толстых томов. По нему очень легко найти номер любого жителя города, но почти невозможно найти по известному номеру абонента. Теперь для каждой буквы из отправляемого сообщения выбирается случайно имя, начинающееся на ту же букву. Таким образом, букве ставится в соответствие номер телефона абонента или шифр. Отправляемое сообщение «КОРОБКА» будет шифроваться следующим образом:

Сообщение	Выбранное имя	Криптотекст
К	Королёв	5643452
О	Орехов	3572651
Р	Рузаева	4673956
O	Осипов	3517289
Б	Батурин	7755628
К	Кирсанова	1235267
А	Арсеньева	8492746

Криптотекстом будет являться цепочка номеров, записанных в порядке их появления в таблице. Из примера следует, что одному и тому же сообщению может соответствовать несколько криптотекстов.

Примеры таких криптотекстов:

Криптотекст 1	Криптотекст 2	Криптотекст 3
1235267	5643452	1235267
3572651	3517289	3517289
4673956	4673956	4673956
3517289	3572651	3572651
7755628	7755628	7755628
5643452	1235267	5643452
8492746	8492746	8492746

Чтобы расшифровать текст, достаточно иметь справочник, составленный согласно возрастанию номеров. Этот справочник является лазейкой (секрет, который помогает получить начальный текст), известной только легальным пользователям. Не имея на руках копии справочника, криптоаналитик затратит очень много времени на расшифровку.^[2]

Схема шифрования с открытым ключом Править

Пусть $ K $ — пространство ключей, а $ e $ и $ d $ — ключи шифрования и расшифрования соответственно. $ E_e $ — функция шифрования для произвольного ключа $ e $$ \in $$ K $, такая что:

$ E_e(m)=c $

Здесь $ c $$ \in $$ C $, где $ C $ — пространство шифротекстов, а $ m $$ \in $$ M $, где $ M $ — пространство сообщений.

$ D_d $ — фукция расшифрования , с помощью которой можно найти исходное сообщение $ m $, зная шифротекст $ c $ :

$ D_d(c)=m $

{$ E_e $: $ e $$ \in $$ K $}- набор шифрования, а {$ D_d $: $ d $$ \in $$ K $} — соответствующий набор для расшифрования. Каждая пара $ (E, D) $ имеет свойство: зная $ E_e $, невозможно решить уравнение $ E_e(m)=c $, то есть для данного произвольного шифротекста $ c $$ \in $$ C $, невозможно найти сообщение $ m $$ \in $$ M $. Это значит, что по данному $ e $ невозможно определить соответствующий ключ расшифрования $ d $. $ E_e $ является односторонней функцией, а $ d $ — лазейкой.^[3]

Ниже показана схема передачи информации лицом А лицу В. Они могут быть как физическими лицами, так и организациями и так далее. Но для более лёгкого восприятия принято участников передачи отождествлять с людьми, чаще всего именуемых Алиса и Боб. Участника, который стремится перехватить и расшифровать сообщения Алисы и Боба, чаще всего называют Евой.

1. Боб выбирает пару $ (e,d) $ и шлёт ключ шифрования $ e $ (открытый ключ) Алисе по открытому каналу, а ключ расшифрования $ d $ (закрытый ключ) защищён и секретен (он не должен передаваться по открытому каналу, либо его подлинность должна быть гарантирована некоторым сертифицирующим органом).
2. Чтобы послать сообщение $ m $ Бобу, Алиса применяет функцию шифрования, определённую открытым ключом $ e $: $ E_e(m)=c $, $ c $ — полученный шифротекст.
3. Боб расшифровывает шифротекст $ c $, применяя обратное преобразование $ D_d $, однозначно определённое значением $ d $.

Начало асимметричным шифрам было положено в работе «Новые направления в современной криптографии» Уитфилда Диффи и Мартина Хеллмана, опубликованной в 1976 году. Находясь под влиянием работы Ральфа Меркле (Ralph Merkle) о рапространении открытого ключа, они предложили метод получения секретных ключей, используя открытый канал. Этот метод экспоненциального обмена ключей, который стал известен как обмен ключами Диффи-Хеллмана, был первым опубликованным практичным методом для установления разделения секретного ключа между заверенными пользователями канала. В 2002 году Хеллман предложил называть данный алгоритм «Диффи — Хеллмана — Меркле», признавая вклад Меркле в изобретение криптографии с открытым ключом. Эта же схема была разработана Малькольмом Вильямсоном в 1970-х, но держалась в секрете до 1997 года. Метод Меркле по распространению открытого ключа был изобретён в 1974 году и опубликован в 1978, его также называют загадкой Меркле.

В 1977 году учёными Рональдом Райвестом (Ronald Linn Rivest), Ади Шамиром (Adi Shamir) и Леонардом Адлеманом (Leonard Adleman) из Массачусетского Технологического Института (MIT) был разработан алгоритм шифрования, основанный на проблеме о разложении на множители. Система была названа по первым буквам их фамилий. Эта же система была изобретена Клиффордом Коксом (Clifford Cocks) в 1973 году, работавшим в центре правительственной связи (GCHQ). Но эта работа хранилась лишь во внутренних документах центра, поэтому о её существовании было не известно до 1977 года. RSA стал первым алгоритмом, пригодным и для шифрования, и для цифровой подписи.

Вообще, в основу известных асимметричных криптосистем кладётся одна из сложных математических проблем, которая позволяет строить односторонние функции и функции-лазейки. Например, криптосистемы

Быстрые криптосистемы с открытым ключом — Википедия

Быстрая криптосистема с открытым ключом (англ. Fast public-key cryptosystem) или лёгкая криптосистема с открытым ключом (англ. Lightweight public-key cryptosystem) — асимметричная криптосистема, используемая в устройствах с ограниченными ресурсами.

Обычные криптографические алгоритмы используются на специальных аппаратных устройствах или настольных компьютерах. Встраиваемые системы, такие как: мобильные телефоны, КПК, смарт-карты, RFID-системы и т. д., обладают ограниченными ресурсами и требуют, для использования в них криптографической защиты, применения других алгоритмов, которые бы использовали меньше памяти, были более быстрыми и эффективнее использовали энергию. Криптосистемы с открытым ключом работают медленнее, чем симметричные криптосистемы. Поэтому при использовании их в мобильных устройствах особенно важно выбрать производительную реализацию.

Одна из наиболее распространенных асимметричных криптосистем — RSA. RSA плохо подходит для использования во встраиваемых устройствах, потому что требует оперирования большими числами, что не всегда можно реализовать при ограниченных ресурсах. Кроме того, RSA работает довольно медленно, особенно это касается генерации ключей, и в RSA используются более длинные ключи по сравнению с другими криптосистемами с открытым ключом. Но RSA хорошо подходит для сравнения криптографической стойкости других криптосистем. Для использования криптографии в мобильных устройствах, память и вычислительная мощность которых сильно ограничены, необходимы более эффективные алгоритмы. Самая распространенная из таких криптосистем — эллиптическая криптосистема, требует меньше ресурсов, чем RSA. Хотя эллиптическая криптосистема не настолько хорошо исследована, как RSA, она считается надежной и используется в нескольких стандартах. Криптосистемы, созданные позднее, такие как: NTRU, Braid Cryptosystem, работают быстрее, чем эллиптическая криптосистема, но их надежность недостаточно исследована.

Основная статья: RSA

NTRU был разработан в середине 1990-х годов и впервые был представлен на конференции CRYPTO’96. NTRU запатентован NTRU Cryptosystems, Inc. 24 июля 2000 года. В этом алгоритме все операции производятся в кольце усечённых многочленов. Криптографическая стойкость алгоритма основана на сложности задачи нахождения короткого вектора в заданной решётке. NTRU работает быстрее, чем используемые в настоящее время криптосистемы с открытым ключом. Для шифрования и расшифрования сообщения длиной N символов необходимо O(N2){\displaystyle O(N^{2})} операций для алгоритма NTRU, в то время как для RSA требуется O(N3){\displaystyle O(N^{3})} операций. Криптографическая стойкость NTRU ещё не достаточно исследована. Кроме того NTRU является ненадёжным алгоритмом, то есть при расшифровании можно получить сообщение, отличающее от того, которое использовалось при шифровании. Криптостойкость NTRU-167 (Параметр N = 167) примерно соответствует RSA-512. Стойкость NTRU-263 и NTRU-503 сопоставима со стойкостью RSA-1024 и RSA-2048 соответственно. При этом при использовании NTRU-263 длина открытого ключа равняется 1841 биту, а секретного — 834 бита. В NTRU зашифрованное сообщение больше открытого текста примерно в 4,5 раза.

Кольцо усечённых многочленов[править | править код]

Различные реализации NTRU характеризуются тремя целыми числами — N, p и q. Числа p и q не обязательно должны быть простыми, но необходимо, чтобы они не имели общих делителей. Базовыми объектами в NTRU являются многочлены порядка N-1 с целочисленными коэффициентами:

a=a0+a1X+a2X2+⋯+aN−1XN−1{\displaystyle a=a_{0}+a_{1}X+a_{2}X^{2}+\cdots +a_{N-1}X^{N-1}}.

Операция сложения определена просто, как сложение коэффициентов при соответствующих степенях:

a+b=(a0+b0)+(a1+b1)X+⋯+(aN−1+bN−1)XN−1{\displaystyle a+b=(a_{0}+b_{0})+(a_{1}+b_{1})X+\cdots +(a_{N-1}+b_{N-1})X^{N-1}}.

Операция умножения определена так же, с помощью умножения коэффициентов при соответствующих степенях, с одной поправкой. При умножении многочленов XN{\displaystyle X^{N}} необходимо заменить на 1, XN+1{\displaystyle X^{N+1}} заменить на X и т. д.:

a⊗b=c0+c1X+⋯+cN−1XN−1{\displaystyle a\otimes b=c_{0}+c_{1}X+\cdots +c_{N-1}X^{N-1}}, где ck=a0bk+a1bk−1+⋯+akb0+ak+1bN−1+ak+2bN−2+⋯+aN−1bk+1{\displaystyle c_{k}=a_{0}b_{k}+a_{1}b_{k-1}+\cdots +a_{k}b_{0}+a_{k+1}b_{N-1}+a_{k+2}b_{N-2}+\cdots +a_{N-1}b_{k+1}}.

Правила сложения и умножения обладают свойством дистрибутивности:

a⊗(b+c)=(a⊗b)+(a⊗c){\displaystyle a\otimes (b+c)=(a\otimes b)+(a\otimes c)}.

Кольцо многочленов с определёнными таким образом операциями сложения и умножения называется кольцом усечённых многочленов. Оно изоморфно кольцу отношений Z[X]/(XN−1){\displaystyle Z[X]/(X^{N}-1)}. В NTRU используются кольца усечённых многочленов с арифметикой по модулю p и q. Это значит, что коэффициенты ai{\displaystyle a_{i}} и bi{\displaystyle b_{i}} складываются и умножаются по модулю.

Генерация ключа[править | править код]

Пусть R — кольцо усечённых многочленов. Если Боб хочет создать пару ключей, он случайно выбирает многочлены f,g∈R{\displaystyle f,g\in R}. Многочлен f должен иметь обратный многочлен по модулю p и q. Если для f не существует обратного, то Боб должен выбрать другой многочлен. Далее Боб должен вычислить обратные многочлены по модулю p и q, обозначим их fp−1{\displaystyle f_{p}^{-1}} и fq−1{\displaystyle f_{q}^{-1}} соответственно. Затем нужно вычислить

h=pfq−1⊗gmodq{\displaystyle h=pf_{q}^{-1}\otimes g\mod q}.

Секретным ключом будет пара f, fp−1{\displaystyle f_{p}^{-1}}, а открытым h.

Шифрование[править | править код]

Если Алиса хочет отправить сообщение Бобу, используя его открытый ключ h, ей необходимо представить сообщение в виде многочлена m, коэффициенты которого взяты по модулю p. Также ей необходимо произвольно выбрать многочлен r. Далее, используя эти параметры, она вычисляет многочлен

e=r⊗h+mmodq{\displaystyle e=r\otimes h+m\mod q}.

Многочлен e является зашифрованным сообщением, которое хочет отправить Алиса.

Расшифрование[править | править код]

Предположим Боб получил зашифрованное сообщение, которое послала ему Алиса. Для начала ему необходимо вычислить

a=f⊗emodq{\displaystyle a=f\otimes e\mod q},

используя известный только ему многочлен f. Теперь Боб может восстановить сообщение Алисы, вычислив

m=fp−1⊗amodp{\displaystyle m=f_{p}^{-1}\otimes a\mod p}.

Как это работает[править | править код]

Рассмотрим почему при расшифровании получается исходное сообщение:

a=f⊗emodq=f⊗r⊗h+f⊗mmodq=f⊗r⊗pfq−1⊗g+f⊗mmodq=pr⊗g+f⊗mmodq{\displaystyle a=f\otimes e\mod q=f\otimes r\otimes h+f\otimes m\mod q=f\otimes r\otimes pf_{q}^{-1}\otimes g+f\otimes m\mod q=pr\otimes g+f\otimes m\mod q}

m=fp−1⊗amodp=fp−1⊗pr⊗g+fp−1⊗f⊗mmodp{\displaystyle m=f_{p}^{-1}\otimes a\mod p=f_{p}^{-1}\otimes pr\otimes g+f_{p}^{-1}\otimes f\otimes m\mod p}

Следует заметить, что при расшифровании может получиться сообщение отличающееся от исходного. Это происходит из-за того, что операции производятся сначала по модулю q, а потом по модулю p. На практике, если правильно выбрать параметры, вероятность возникновения такой ошибки становится меньше, чем 2−100{\displaystyle 2^{-100}}.

Дополнение[править | править код]

Рекомендации[править | править код]

1. Авторы криптосистемы NTRU рекомендуют использовать в качестве коэффициентов для многочленов f, g и m числа из множества {-1,0,1}. Такой подход позволяет оптимизировать хранение данных в памяти компьютера, ускорить некоторые вычисления и не сказывается на криптостойкости системы.
2. В то же время, данная рекомендация не распространяется на многочлен r. Напротив, для улучшения обфускации оригинального сообщения рекомендуется не ограничиваться числами из множества {-1,0,1}. Однако и слишком большие числа брать не следует, ведь вычисления все равно будут проводиться по модулю.
3. Использование числа -1 в качестве коэффициента опционально, так как оно особенно удобно в троичной системе счисления, но не слишком — в двоичной.
4. Что касается больших чисел, то криптостойкость алгоритма NTRU основана не на длинах модулей p и q, а на значении числа N. Из этого следует, что не обязательно использовать большие целые числа в качестве модулей. Можно ограничиться числами до 512 включительно. Однако N следует брать относительно большое. На данный момент (конец 2011 года) для максимальной криптостойкости рекомендуется брать N⩾500{\displaystyle N\geqslant 500}. Здесь 500 — не длина числа N в битах, а непосредственное значение.

Оптимизация[править | править код]

1. Во-первых, если внимательно посмотреть на используемые для шифрования и расшифрования формулы, то нетрудно заметить, что многочлен fq−1{\displaystyle f_{q}^{-1}} успешно сокращается и нигде более не используется. А значит, можно не тратить время на его вычисление.
2. Во-вторых, раз уж нам более не нужно вычислять fq−1{\displaystyle f_{q}^{-1}}, значит мы можем выбрать число q так, чтобы было наиболее удобно вести расчеты по этому модулю. Логичнее всего использовать степени двойки. Например, 64, 128, 256 и т.д. Тогда, вместо медленной операции взятия остатка от деления можно будет использовать быструю операцию побитового «и» (или аналогичную).
3. В-третьих, в описании алгоритма сказано, что модули p и q не обязательно должны быть простыми, достаточно, чтобы они были взаимно простыми. А это значит, что для некоторого непростого p в кольце чисел по этому модулю p обязательно найдутся необратимые элементы. Подобный недостаток может сказаться на поиске многочлена fp−1{\displaystyle f_{p}^{-1}}. Чтобы избежать подобной проблемы, рекомендуется использовать простые числа. Причем не обязательно тратить время на генерирование простого числа (методы проверки на простоту слишком медленные, чтобы их использовать без причины), достаточно брать значение p из множества {3,5,7,11,…}.

Возможные ошибки[править | править код]

Во время этапа расшифровки нужно быть особенно внимательным с коэффициентами многочлена a{\displaystyle a}. Все коэффициенты должны находиться в интервале [-q/2, q/2], а не [0, q-1]. Если не сделать подобную проверку, то могут получиться разные результаты. В этом нетрудно убедиться. Пусть, мы имеем следующий многочлен a{\displaystyle a}:

a=3−7X−10X2−11X3+10X4+7X5+6X6+7X7+5X8−3X9−7X10(mod32){\displaystyle {\textbf {a}}=3-7X-10X^{2}-11X^{3}+10X^{4}+7X^{5}+6X^{6}+7X^{7}+5X^{8}-3X^{9}-7X^{10}{\pmod {32}}}

Записанный таким образом многочлен полностью соответствует заявленному условию. Теперь выпишем возможный «ошибочный» вариант:

a=3+25X+22X2+21X3+10X4+7X5+6X6+7X7+5X8+29X9+28X10(mod32){\displaystyle {\textbf {a}}=3+25X+22X^{2}+21X^{3}+10X^{4}+7X^{5}+6X^{6}+7X^{7}+5X^{8}+29X^{9}+28X^{10}{\pmod {32}}}

Казалось бы, мы не сделали никаких неравносильных преобразований. Однако, достаточно просто взять все коэффициенты по модулю p (а это, фактически, следующее действие расшифровки), как сразу станет понятна суть ошибки. Допустим, p = 3. Тогда «правильное» выражение преобразуется в следующее:

a=2X+2X2+X3+X4+X5+X7+2X8+2X10(mod3){\displaystyle {\textbf {a}}=2X+2X^{2}+X^{3}+X^{4}+X^{5}+X^{7}+2X^{8}+2X^{10}{\pmod {3}}}

А ошибочное в следующее:

a=X+X2+X4+X5+X7+2X8+2X9+X10(mod3){\displaystyle {\textbf {a}}=X+X^{2}+X^{4}+X^{5}+X^{7}+2X^{8}+2X^{9}+X^{10}{\pmod {3}}}

Очевидно, что дальнейшая работа с каждым из полученных многочленов даст разные результаты. Разница в том, что первый многочлен позволит вычислить правильное исходное сообщение, а второй — искаженное.

Криптосистема, основанная на группе кос[править | править код]

Идея создания криптосистемы, основанной на группе кос, была описана на конференции CRYPTO’2000. Она основана на сложности задачи поиска обобщенного сопряженного в группе кос.

Для шифрования и расшифрования используется хеш-функция H:Bl+r→{0,1}k{\displaystyle H:B_{l+r}\rightarrow \{0,1\}^{k}}. Эта хеш-функция не должна содержать коллизий. В криптосистеме, основанной на группе кос, используется свойство коммутативности кос построенных в LBl{\displaystyle LB_{l}}, то есть в группе n-кос, построенной с использованием только генераторов меньших, чем некоторое целое число d, и в RBr{\displaystyle RB_{r}}, то есть в группе n-кос, построенной с использованием только генераторов больших, чем d.

Генерация ключа[править | править код]

Выбирается достаточно сложная (l+r)-коса x∈Bl+r{\displaystyle x\in B_{l+r}}. Далее выбирается коса a∈LBl{\displaystyle a\in LB_{l}}. Открытым ключом является пара (x, y), где y=axa−1{\displaystyle y=axa^{-1}}. Секретным ключом является a.

Шифрование[править | править код]

Пусть необходимо отправить сообщение m∈{0,1}k{\displaystyle m\in \{0,1\}^{k}}, зашифровав его с помощью ключа (x, y). Тогда необходимо произвольно выбрать b∈RBr{\displaystyle b\in RB_{r}}. Шифротекстом будет пара (c, d), где c=bxb−1{\displaystyle c=bxb^{-1}} и d=H(byb−1)+m{\displaystyle d=H(byb^{-1})+m}.

Расшифрование[править | править код]

Чтобы расшифровать сообщение (c, d), используя ключ a необходимо, вычислить m=H(aca−1)+d{\displaystyle m=H(aca^{-1})+d}.

ECC и RSA на восьмибитном процессоре[править | править код]

ECC, по сравнению с RSA, лучше подходит для применения в мобильных устройствах, так как она работает быстрее, использует ключи меньшей длины и потребляет меньше памяти и энергии. В RSA используется арифметика в кольце целых чисел, и в её основу положена трудность разложения больших целых чисел на множители. В ECC используются группы точек эллиптических кривых, и её стойкость основана на сложности дискретного логарифмирования. В настоящее время не известны алгоритмы нахождения дискретного логарифма на эллиптической кривой с суб-экспоненциальной сложностью, в то время как для разложения на множители такие алгоритмы существуют. Это позволяет использовать ключи для ECC меньшей длины, чем для RSA. ECC-160 обеспечивает примерно такой же уровень безопасности, как RSA-1024. Но в то же время увеличение длины ключа ECC в два раза приводит к большему увеличению криптостойкости, чем увеличение в два раза длины ключа RSA. Из-за этого ECC-224 примерно соответствует RSA-2048, а значит в будущем преимущества ECC только возрастут. Также увеличение длины ключа и уменьшение разрядности процессора приводит к увеличению преимущества в производительности ECC перед RSA.

В статье «Comparing Elliptic Curve Cryptography and RSA on 8-bit CPUs» проводилось сравнение производительности и использования памяти ECC и RSA реализованных для восьмибитных процессоров. Производительность сравнивается на двух процессорах: Chipcon CC1010 и Atmel ATmega128. Результаты сравнения сведены в таблицу. Для шифрования RSA использовался открытый ключ e=216+1{\displaystyle e=2^{16}+1}.

Алгоритм	ATmega128 @ 8МГц			CC1010 @ 14,7456 МГц
	Время, с	Память под данные, байтов	Память под код, байтов	Время, с	Память под данные, байтов	Память под код, байтов
ECC-160	0,81	282	3682	4,58	180+86	2166
ECC-192	1,24	336	3979	7,56	216+102	2152
ECC-224	2,19	422	4812	11,98	259+114	2214
RSA-1024 шифрование	0,43	542	1073	> 4,48
RSA-1024 расшифрование	10,99	930	6292	~ 106,66
RSA-2048 шифрование	1,94	1332	2854
RSA-2048 расшифрование	83,26	1853	7736

RSA, ECC, NTRU и криптосистема в группе кос[править | править код]

В статье «Practical comparison of fast public-key cryptosystems» было проведено сравнение четырех криптосистем. Авторы написали свои реализации ECC, NTRU и криптосистемы в группе кос. Результаты для RSA были взяты из тестов производительности библиотеки J/Crypto, поэтому код RSA был лучше оптимизирован, чем код остальных криптосистем.

	RSA-1024	ECC-168	NTRU-263	Криптосистема в группе кос
Увеличение сообщения	1	2	≈4,5{\displaystyle \approx 4,5}	4
Длина блока, битов	1024	160	416	1088
Длина открытого ключа, битов	1024	169	1841	1000
Скорость генерации ключа, мс	1432	65	19,8	8,5
Скорость шифрования, мс	4,28	140	1,9	29,8
Скорость расшифрования, мс	48,5	67	3,5	14,9

• Priit Karu, Jonne Loikkanen. Practical comparison of fast public-key cryptosystems. Helsinki University of Technology, 2001.
• Ki Hyoung Ko, Sang Jin Lee, Jung Hee Cheon, Jae Woo Han, Ju-sung Kang, and Choonsik Park. New Public-key Cryptosystem Using Braid Groups. Proceedings of Crypto 2000, LNCS 1880 (2000).
• Jeffrey Hoffstein, Jill Pipher, Joseph H. Silverman. NTRU: A Ring-Based Public Key Cryptosystem. Proceedings of ANTS , Portland (1998), Springer-Verlag.
• Jeffrey Hoffstein, Jill Pipher and Joseph H. Silverman. NTRU: A Public Key Cryptosystem. August 1999.
• Joseph H. Silverman, W. Whyte. NTRU Report 018. Estimating Decryption Failure Probabilities for NTRUEncrypt. June 20, 2003.
• Nils Gura, Arun Patel, Arvinderpal Wander, Hans Eberle, Sheueling Chang Shantz. Comparing Elliptic Curve Cryptography and RSA on 8-bit CPUs. Workshop on Cryptographic Hardware and Embedded Systems (CHES 2004), LNCS 3156, pp. 119–132, 2004.

Криптография с открытым ключом

Криптографическая система с открытым ключом или Асимметричное шифрование, Асимметричный шифр — это система шифрования или электронной цифровой подписи (ЭЦП), при которой открытый ключ передаётся по незащищенному от постороннего наблюдения каналу, и используется для проверки ЭЦП и шифрования сообщения. Генерация и расшифровака сообщения осуществляется посредством секретного ключа.

Основы криптографии с открытым ключом были сформулированы совсем недавно. Идею создания криптографии с открытым ключом выдвинули Уитфилдом Диффи (Whitfield Diffie), Мартином Хеллманом (Martin Hellman) и Ральфом Мерклом (Ralph Merkle). По их убеждению, ключи можно использовать парами — ключ шифрования и ключ дешифрования, благодаря чему получлить один ключ из другого не представляется возможным. В 1976 году Диффи и Хеллман впервые представили эту идею на Национальной компьютерной конференции, а всего через несколько месяцев была опубликована их основополагающая работа «Новые направления в криптографии» («New Directions in Cryptography»).



---

Схема передачи информации лицом А лицу В

Большая часть безопасных алгоритмов основано на так называемых необратимых функциях. В криптографии под необратимыми функциями подразумевают, невозможность получения обратного значения с помощью современной техники за обозримый интервал времени. Все известные и действующие на настоящий момент системы с открытым ключом базируются на одном из трех типов необратимых преобразований:

• Разложение больших чисел на простые множители (RSA)
• Вычисление логарифма в конечном поле (криптосистема Эль-Гамаля)
• Вычисление корней алгебраических уравнений (на основе эллиптических уравнений)

Криптосистемы с открытым ключом в последнее время широко применяются в качестве самостоятельных средств защиты передаваемых и хранимых данных, как средство для распределения ключей и средства аутентификации пользователей.

Все современные криптосистемы с открытым ключом весьма медлительны и практически ни одна из них не может сравниться по быстродействию с симметричными криптосистемами. Быстродействие RSA в тысячи раз ниже, чем у DES или ГОСТ 28147-89. Поэтому эффективнее использовать гибридные криптосистемы.



---

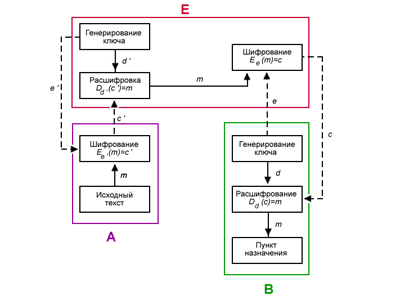
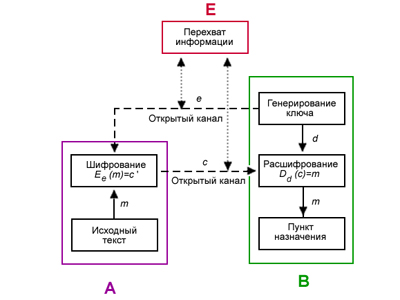
Рисунок иллюстрирует, как кто-то, выполняющий роль активного перехватчика, может захватить систему без взламывания системы шифрования

Существует пять основных принципов построения криптосистем с открытым ключом:

• Начальный этап — решение трудной задачи P. Сложность этой задачи заключается в отсутствие алгоритма, который мог бы подобрать все возможные варианты решения задачи P за полиномиальное время относительно размера задачи.
• Решение легкой подзадачи P’ из P, которое должно быть осуществлено за линейное время.
• «Перетасовываем и взбалтываем» P’. Для того, чтобы получить задачу P’’, абсолютно отличную от первоначальной, необходима задача P’’ ввиде оригинальной труднорешаемой задачи P.
• Использование P’’ с описанием в роли ключа шифрования. Процесс получения P’ из P’’ держится в секрете как секретная лазейка.
• В итоге, криптосистема организована таким образом, что алгоритмы расшифрования для легального пользователя и криптоаналитика существенно различны. В то время как первый решает P’’ задачу, второй использует секретную лазейку и решает P’ задачу.

Для того, чтобы понять идеи и методы криптографии с открытым ключом необходимо привести следующий пример — хранение паролей в компьютере. У каждого пользователь в сети имеется свой секретный пароль. При входе в сеть, пользователь указывает свое имя и вводит пароль. Важно отметить, что хранение пароля на жестком диске компьютера облегчает доступ злоумышленников к секретной информации. Как уже говорилось, для решения задачи используется односторонняя или необратимая функция. В процессе создания секретного пароля в компьютере сохраняется не сам пароль, а результат вычисления функции от этого пароля и имени пользователя. Приведем наглядный пример, пользователь Маруся придумала пароль «Баранки». При сохранении этих данных вычисляется результат функции f(МАРУСЯБАРАНКИ), пусть в результате вычисления будет выбрана строка Сухари, которая и будет сохранена в системе. В результате файл паролей будет иметь следующий вид:

Имя f(имя_пароль) МАРУСЯ СУХАРИ

Вход в систему выглядит так:

Имя: АЛИСА Пароль: БАРАНКИ

При введении пользователем Маруся секретного пароля, компьютер проверяет, даёт или нет функция, применяемая к МАРУСЯБАРАНКИ, правильный результат Сухари, хранящийся на диске компьютера. Изменение одной буквы в пароле или имени приведет к совершенно другому результату функции.

В другом примере будет рассмоторена возможность восстановление открытого сообщения с помощью «секретной лазейки», то есть труднодоступной информации. Для шифрования текста можно воспользоваться большим абонентским справочником, который состоит из нескольких толстых томов. Этот справочник позволяет без труда найти номер любого жителя города, однако найти абонента по известному номеру практически невозможно. Итак, для каждой буквы шифруемого сообщения подбирвается имя, начинающееся на ту же букву. В результате, каждой букве соответствует номер телефона абонента. К примеру, отправляемое сообщение «ВОРОНКА» будет зашифровано следующим образом:

Сообщение	Выбранное имя	Криптотекст
В	Волков	5643452
О	Орлов	3572651
Р	Рудакова	4673956
O	Остапов	3517289
Н	Наутин	7755628
К	Киреева	1235267
А	Артемьева	8492746

Криптотекстом представляет собой цепочку номеров, записанных в порядке их выбора в справочнике. Для затруднения дешифрации лучше всего подобрать случайные имена, начинающиеся на нужную букву. Таким образом, исходное сообщение может быть зашифровано множеством криптотекстов (различных списков номеров).



---

Еще одна форма атаки — вычисление закрытого ключа, зная открытый

Для успешной дешифрации текста, необходимо иметь справочник, составленный по возрастанию номеров. В таком случае телефонный справочник является секретной лазейкой, которая помогает получить исходный текст, известной только легальным пользователям. Отсутствие справочника или его копии значительно увеличит время криптоаналитика на расшифровку.

К главным достоинствам ассиметричных шифров относятся:

• Отсутствие необходимости предварительной передачи секретного ключа по надёжному каналу.
• В ассиметричной криптосистеме только один ключ держится в секрете.
• В ассиметричных криптосистемах пару секретных ключей можно не менять на протяжении длительного периода времени.
• Количество ключей в асимметричной криптосистеме значительно меньше, чем в симметричной.

Однако ассиметричная система шифрования имеет и ряд недостатков. Среди них выделяют:

• Сложность внесения изменений в ассиметричный алгоритм шифрования.
• При достаточной надежности шифрования, получатель и отправитель самим фактом пересылки шифрованного сообщения ставят под угрозу безопасность собственной секретной информации.
• Использование длинных ключей в асимметричных алгоритмах.
• Невысокая скорость процесса шифрования-расшифрования с использованием пары ключей.
• Необходимость значительно больших вычислительных ресурсов для ассиметрических криптосистем.

Как работает асимметричное шифрование понятным языком | Безопасность

Мало кто знает как именно работает асимметричное шифрование. К примеру есть люди которые не считают протокол https какой-либо адекватной защитой передаваемых данных. И как правило на попытку убедить в обратном, они отвечают что-то в духе «если мы передаем зашифрованные данные, то мы должны сказать как их расшифровывать, а эту информацию можно перехватить и, следовательно, расшифровать данные». А на аргументы, что это не так и в основу положено асимметричное шифрование, поступает ответ «Ну и что?».

Ладно, я понимаю, знать все тонкости реализации асимметричного шифрования нужно далеко не всем. Но общий принцип работы, я считаю, должен знать каждый, кто как-либо связан с компьютерами.

Хочу вынести суть данного поста в эту аннотацию: Запомните, асимметричное шифрование безопасно, естественно при выполнении всех условий. И чтобы доказать это я попробую описать алгоритм понятным языком, чтобы каждый смог понять, что он безопасен. Встречайте Алису, Боба и Еву и передачу их секретного сообщения под катом.

Кстати почему Алиса и Боб? Об этом есть кратенькая статья на википедии: Алиса, Боб и Ева. Чтобы было понятнее, Алиса и Боб хотят обменяться сообщениями, а Ева пытается эти сообщения перехватить и прочесть.

Немного истории

Криптография прошлых веков имела одну огромную проблему — проблема передачи ключей. В те времена существовали только так называемые «симметричные» шифры — шифры при котором данные шифруются и расшифровываются одним и тем же ключом.

К примеру, Алиса зашифровала некоторое сообщение и хочет отправить его Бобу. Естественно, чтобы Боб его прочитал, ему нужен ключ которым было зашифровано данное сообщение. И тут возникает проблема, как передать ключ чтобы его никто не смог перехватить. Пытливые умы предложат — пусть передают при личной встрече, а потом общаются сколько захотят. Да, не спорю, выход. А теперь представьте на секунду, что ваша интернет почта, перед тем как вы авторизируетесь в ней, потребует вашей поездки до физического местоположения сервера с почтой. Удобно? Пожалуй не очень.

Конечно ключ можно передавать по другому каналу связи. Но криптография рассматривает все незащищенные каналы связи как небезопасные. То есть передача ключа Бобу по телефону, например, считается небезопасной так, как ничто не мешает Еве прослушивать и телефон в том числе.

До 70-ых годов, эта проблема настолько стала привычной, что считался аксиомой тот факт, что для передачи сообщения нужно передавать и ключ которым сообщение зашифровано (причем некоторых люди до сих пор считают именно так). Но в 76 году Диффи и Хеллман предложили свой «метод экспоненциального обмена ключей». С этих годов и началось развитие асимметричных криптосистем.

Немножко реальной жизни

Прежде чем изучать какой либо алгоритм, нужно представить как он работает. И самый простой способ — это сравнить его с работой чего-то в реальности.

Представим что Алиса и Боб живут в стране, в которой вся почтовая система абсолютно аморальна и почтовые служащие читают всю незащищенную корреспонденцию. Алиса, девочка не глупая, прежде чем отправить сообщение Бобу, взяла железный ящик и, положив внутрь письмо и закрыв его на свой замок, отправляет этот ящик Бобу.

Естественно на почте прочитать это письмо не могут, но его не может прочитать и сам Боб, так как у него нет ключа которым закрыт замок. Алиса, конечно, может взять еще один железный ящик, положить в него ключ от предыдущего, и отправить его Бобу, но его Боб тоже не сможет открыть…

Единственный путь это все же сделать дубликат ключа и дать его Бобу при личной встрече…

И вот начинает казаться что обмен ключами является неизбежной частью шифрования — или все-таки нет?

Представим другую картину. Распишу пошагово:

1. Алиса кладет свое письмо в железный ящик и, заперев его на замок, отправляет Бобу.
2. Боб при получении ящика, (внимание!) берет свой замок и, дополнительно заперев им ящик, отправляет обратно.
3. Алисе ящик приходит уже с двумя замками (напомню с первым замком Алисы от которого у нее есть ключ, и со вторым — Боба, от которого ключ есть есть только у Боба).
4. Алиса снимает свой замок, и отправляет ящик обратно Бобу
5. Бобу приходит ящик с уже одним его замком от которого у него есть ключ
6. Боб отпирает оставшийся его замок своим ключом, и читает сообщение

Значение этой кратенькой истории огромно. Она показывает что два человека могут передавать секретное сообщение без обмена ключами. Вдумайтесь! Эта история фактически рушит все аксиомы на которых была построена тогдашняя криптография. Да мы получаем некоторое усложнение процесса (ящик пришлось пересылать три раза), но результат…

Вернемся к криптографии

Казалось бы решение найдено. Отправитель и принимающий шифруют свое сообщение, и затем собеседники поочередно снимают свой шифр.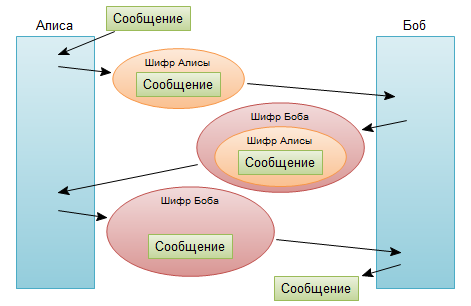

Но суть в том что не существуют таких шифров, которые бы позволили снять шифр из под другого шифра. То есть этап где Алиса снимает свой шифр невозможен: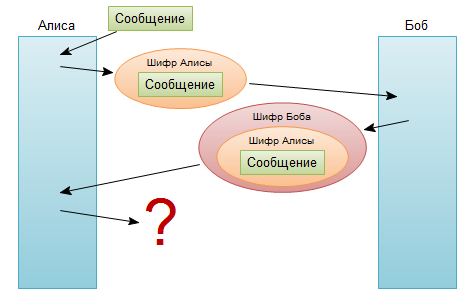

К сожалению, все имеющиеся алгоритмы до сих пор требуют снятия шифров в той очереди в которой они были применены. Боюсь назвать это аксиомой (так как история уже знает случаи когда такие аксиомы разбивались в пух и прах), но это так до сих пор.

Вернемся к математике

Идея с ящиком, о которой я описывал выше, вдохновили Диффи и Хеллмана искать способ передачи сообщения. В конце концов они пришли к использованию односторонних функций.

Что такое односторонняя функция? К примеру есть функция удвоение, т.е удвоить(4)=8, она двухсторонняя, т.к. из результата 8 легко получить исходное значение 4. Односторонняя функция — та функция после применения которой практически невозможно получить исходное значение. К примеру смешивание желтой и синей краски — пример односторонней функции. Смешать их легко, а вот получить обратно исходные компоненты — невозможно. Одна из таких функций в математике — вычисление по модулю.

За основу алгоритма Хеллман предложил функцию Y^x (mod P). Обратное преобразование для такой функции очень сложно, и можно сказать что, по сути, заключается в полном переборе исходных значений.

К примеру вам сказали, что 5 ^x (mod 7) = 2, попробуйте найдите x, а? Нашли? А теперь представьте что за Y и P взяты числа порядка 10³⁰⁰.

Кстати сказать, для повышения стойкости, число P должно являться простым числом, а Y — являться первообразным корнем по модулю P. Но так как мы все же пытаемся понять теорию, то смысла заморачиваться на этом я не вижу.

Алгоритм Диффи-Хеллмана

И вот однажды Хеллмана осенило и он смог разработать рабочий алгоритм обмена ключами. Для работы по этому алгоритму нужно выполнять шаги на обоих сторонах, поэтому я зарисую это в таблице:

	Алиса	Боб
Этап 1	Оба участника договариваются о значениях Y и P для общей односторонней функции. Эта информация не является секретной. Допустим были выбраны значения 7 и 11. Общая функция будет выглядеть следующим образом: 7x (mod 11)
Этап 2	Алиса выбирает случайное число, например 3, хранит его в секрете, обозначим его как число A	Боб выбирает случайное число, например 6, хранит его в секрете, обозначим его как число B
Этап 3	Алиса подставляет число A в общую функцию и вычисляет результат 73 (mod 11) = 343 (mod 11) = 2, обозначает результат этого вычисления как число a	Боб подставляет число B в общую функцию и вычисляет результат 76 (mod 11) = 117649 (mod 11) = 4, обозначает результат этого вычисления как число b
Этап 4	Алиса передает число a Бобу	Боб передает число b Алисе
Этап 5	Алиса получает b от Боба, и вычисляет значение bA (mod 11) = 43 (mod 11) = 64 (mod 11) = 9	Боб получает a от Алисы, и вычисляет значение aB (mod 11) = 26 (mod 11) = 64 (mod 11) = 9
Этап 6	Оба участника в итоге получили число 9. Это и будет являться ключом.

Магия? Не спорю, с первого взгляда непонятно. Но после вчитывания и вдумывания в эту таблицу становится понятно как это работает. Впрочем если понятно не стало, то пролистайте до конца главы, там я выложил поясняющее видео.

Причем обратите внимание, что для получения ключа в конечной формуле, любому человеку нужно иметь три значения:

• Значения a и P, и секретное число Боба B
• или значения b и P, и секретное число Алисы A

Но секретные числа по каналу не передаются! Еве не получится восстановить ключ, не имея чьего-нибудь секретного числа. Почему — я писал выше, данная функция является односторонней. Попробуйте решите уравнение 4^x (mod 11) = 2^y (mod 11) найдя x и y.

Чтобы было понятнее, как работает схема Хеллмана, представьте шифр, в котором в качестве ключа каким-то образом используется цвет:

Допустим вначале, что у всех, включая Алису, Боба и Еву, имеется трехлитровая банка, в которую налит один литр желтой краски. Если Алиса и Боб хотят договориться о секретном ключе, они добавляют в свои банки по одному литру своей собственной секретной краски.

Алиса может добавить краску фиолетового оттенка, а Боб — малинового. После этого каждый из них посылает свою банку с перемешанным содержимым другому.

И наконец, Алиса берет смесь Боба и подливает в нее один литр своей секретной краски, а Боб берет смесь Алисы и добавляет в нее один литр своей секретной краски. Краска в обеих банках теперь станет одного цвета, поскольку в каждой находится по одному литру желтой, фиолетовой и малиновой краски.

Именно этот цвет, полученный при добавлении дважды в банки красок, и будет использоваться как ключ. Алиса понятия не имеет, какую краску добавил Боб, а Боб также не представляет, какую краску налила Алиса, но оба они достигли одного и того же результата.

Между тем Ева в ярости. Даже если она и сумеет перехватить банки с промежуточным продуктом, ей не удастся определить конечный цвет, который и будет согласованным ключом. Ева может видеть цвет краски, полученной при перемешивании желтой краски и секретной краски Алисы в банке, отправленной Бобу, и она может видеть цвет краски, полученной при перемешивании желтой краски и секретной краски Боба в банке, отправленной Алисе, но чтобы найти ключ, ей, на самом деле, необходимо знать цвета исходных секретных красок Алисы и Боба. Однако, рассматривая банки с перемешанными красками, Ева не сможет определить секретные краски Алисы и Боба. Даже если она возьмет образец одной из смешанных красок, ей не удастся разделить ее на исходные краски, чтобы найти секретную, поскольку смешивание краски является односторонней функцией.

Все равно непонятно? Тогда смотрим видео:


Что же, надеюсь, вы поняли, что существует вполне реальный способ безопасного обмена ключами. Но прошу заметить, назвать этот алгоритм асимметричным шифром пока нельзя, так как по сути это всего лишь алгоритм обмена ключами.

Асимметричное шифрование

асимметричный алгоритм предполагает под собой наличие двух ключей — публичного и приватного. То есть сообщение шифруется публичным ключом, а расшифровывается приватным и ни как иначе. Собственно именно эту концепцию сформулировал Диффи.

В общем суть данного алгоритма заключается в том, что принимающая сторона перед приемкой сообщения генерирует пару ключей на основе алгоритма модульной арифметики (принцип такой же как и в алгоритме Диффи-Хеллмана), собственно приватный и публичный ключ. Отправитель перед отправкой получает публичный ключ и шифрует сообщение данным ключом, после чего данное сообщение можно расшифровать только приватным ключом, который хранится в секрете у принимающей стороны.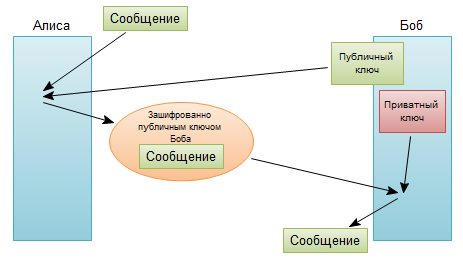

Если вернуться к аналогии с замками, то шифрование с открытым ключом можно представить себе следующим образом:

Любой способен запереть замок, просто защелкнув его, чтобы он закрылся, но отпереть его может только тот, у кого есть ключ. Запереть замок (зашифровывание) легко, почти все могут это сделать, но открыть его (расшифровывание) имеет возможность только владелец ключа. Понимание того, как защелкнуть замок, чтобы он закрылся, ничего не скажет вам, как его отпереть.

Можно провести и более глубокую аналогию.

Представьте, что Алиса проектирует замок и ключ. Она бдительно охраняет ключ, но при этом изготавливает тысячи дубликатов замков и рассылает их по почтовым отделениям по всему миру. Если Боб хочет послать сообщение, он кладет его в коробку, идет на местный почтамт, просит «замок Алисы» и запирает им коробку. Теперь уже ему не удастся открыть коробку, но когда коробку получит Алиса, она сможет открыть ее своим единственным ключом.

Замок и защелкивание его, чтобы он закрылся, эквивалентны общему ключу для зашифровывания, поскольку все имеют доступ к замкам и все могут воспользоваться замком, чтобы закрыть сообщение в коробке. Ключ от замка эквивалентен секретному ключу для расшифровывания, потому что он имеется только у Алисы, только она сможет открыть замок, и только она сможет получить доступ к находящемуся в коробке сообщению.

Есть несколько алгоритмов реализующих асимметричное шифрование. Самый известный из них — RSA. Расписывать его я не вижу смысла, так как понять как он работает с ходу все равно не получится, да и лучше чем написано на википедии я написать все равно не смогу.

Заключение

Что же, надеюсь что, поняв как работает асимметричное шифрование изнутри, вы станете больше ему доверять и соответственно чаще пользоваться SSL =)

Использовались материалы из книги Сингх Саймон — Книга шифров. Кстати, самая лучшая книга для тех кто хочет хотя бы чуточку разбираться в криптографии. Всем советую прочитать.

Позволю себе вставить ссылку на один из прошлых моих постов: Коллизии хеш функций? асимметричное шифрование решает! — пример «нестандартного» применения асимметричного шифрования.

Спасибо за внимание =)

RSA — Википедия

RSA (аббревиатура от фамилий Rivest, Shamir и Adleman) — криптографический алгоритм с открытым ключом, основывающийся на вычислительной сложности задачи факторизации больших целых чисел.

Криптосистема RSA стала первой системой, пригодной и для шифрования, и для цифровой подписи. Алгоритм используется в большом числе криптографических приложений, включая PGP, S/MIME, TLS/SSL, IPSEC/IKE и других^[3].

Опубликованная в ноябре 1976 года статья Уитфилда Диффи и Мартина Хеллмана «Новые направления в криптографии» (англ. New Directions in Cryptography)^[4] перевернула представление о криптографических системах, заложив основы криптографии с открытым ключом. Разработанный впоследствии алгоритм Диффи — Хеллмана позволял двум сторонам получить общий секретный ключ, используя незащищенный канал связи. Однако этот алгоритм не решал проблему аутентификации. Без дополнительных средств пользователи не могли быть уверены, с кем именно они сгенерировали общий секретный ключ.

Изучив эту статью, трое учёных Рональд Ривест, Ади Шамир и Леонард Адлеман из Массачусетского технологического института (MIT) приступили к поискам математической функции, которая бы позволяла реализовать сформулированную Уитфилдом Диффи и Мартином Хеллманом модель криптографической системы с открытым ключом. После работы над более чем 40 возможными вариантами им удалось найти алгоритм, основанный на различии в том, насколько легко находить большие простые числа и насколько сложно раскладывать на множители произведение двух больших простых чисел, получивший впоследствии название RSA. Система была названа по первым буквам фамилий её создателей.

В августе 1977 года в колонке «Математические игры» Мартина Гарднера в журнале Scientific American, с разрешения Рональда Ривеста^[5] появилось первое описание криптосистемы RSA^[6]. Читателям также было предложено дешифровать английскую фразу, зашифрованную описанным алгоритмом:

9686 1477 8829 7431 0816 3569 8962 1829

9613 1409 0575 9874 2982 3147 8013 9451

7546 2225 9991 6951 2514 6622 3919 5781

2206 4355 1245 2093 5708 8839 9055 5154

В качестве открытых параметров системы были использованы числа n= (129 десятичных знаков, 425 бит, также известно как RSA-129) и e=9007. За расшифровку была обещана награда в 100 долларов США. По заявлению Ривеста, для факторизации числа потребовалось бы более 40 квадриллионов лет^[7][3]. Однако чуть более чем через 15 лет, 3 сентября 1993 года было объявлено о запуске проекта распределённых вычислений с координацией через электронную почту по нахождению сомножителей числа RSA-129 и решению головоломки. На протяжении полугода более 600 добровольцев из 20 стран жертвовали процессорное время 1600 машин (три из которых были факс-машинами^{[источник не указан 1547 дней]}). В результате были найдены простые множители и расшифровано исходное сообщение, которое представляет собой фразу «THE MAGIC WORDS ARE SQUEAMISH OSSIFRAGE (англ.)» («Волшебные слова — это брезгливый ягнятник»)^[8][9]. Полученную награду победители пожертвовали в фонд свободного программного обеспечения.

После публикации Мартина Гарднера полное описание новой криптосистемы любой желающий мог получить, выслав по почте запрос Рональду Ривесту с приложенным конвертом с обратным адресом и марками на 35 центов.^[6] Полное описание новой криптосистемы было опубликовано в журнале «Communications of the ACM» в феврале 1978 года^[10].

Заявка на патент была подана 14 декабря 1977 года, в качестве владельца был указан MIT. Патент 4405829 был выдан 20 сентября 1983 года, а 21 сентября 2000 года срок его действия истёк^[11]. Однако за пределами США у изобретателей патента на алгоритм не было, так как в большинстве стран его необходимо было получить до первой публикации^[12].

В 1982 году Ривест, Шамир и Адлеман организовали компанию RSA Data Security (англ.) (в настоящий момент — подразделение EMC). В 1989 году RSA, вместе с симметричным шифром DES, упоминается в RFC 1115, тем самым начиная использование алгоритма в зарождающейся сети Internet^[13], а в 1990 году использовать алгоритм начинает министерство обороны США^[14].

В ноябре 1993 года открыто публикуется версия 1.5 стандарта PKCS1 (англ.), описывающего применение RSA для шифрования и создания электронной подписи. Последние версии стандарта также доступны в виде RFC (RFC 2313 — 1.5, 1993 год; RFC 2437 — 2.0, 1998 год; RFC 3447 — 2.1, 2002 год).

В декабре 1997 года была обнародована информация, согласно которой британский математик Клиффорд Кокс (Clifford Cocks), работавший в центре правительственной связи (GCHQ) Великобритании, описал криптосистему, аналогичную RSA в 1973 году^[15].

Введение[править | править код]

Криптографические системы с открытым ключом используют так называемые односторонние функции, которые обладают следующим свойством:

• если известно x{\displaystyle x}, то f(x){\displaystyle f(x)} вычислить относительно просто;
• если известно y=f(x){\displaystyle y=f(x)}, то для вычисления x{\displaystyle x} нет простого (эффективного) пути.

Под односторонностью понимается не теоретическая однонаправленность, а практическая невозможность вычислить обратное значение, используя современные вычислительные средства, за обозримый интервал времени.

В основу криптографической системы с открытым ключом RSA положена сложность задачи факторизации произведения двух больших простых чисел. Для шифрования используется операция возведения в степень по модулю большого числа. Для дешифрования (обратной операции) за разумное время необходимо уметь вычислять функцию Эйлера от данного большого числа, для чего необходимо знать разложение числа на простые множители.

В криптографической системе с открытым ключом каждый участник располагает как открытым ключом (англ. public key), так и закрытым ключом (англ. private key). В криптографической системе RSA каждый ключ состоит из пары целых чисел. Каждый участник создаёт свой открытый и закрытый ключ самостоятельно. Закрытый ключ каждый из них держит в секрете, а открытые ключи можно сообщать кому угодно или даже публиковать их. Открытый и закрытый ключи каждого участника обмена сообщениями в криптосистеме RSA образуют «согласованную пару» в том смысле, что они являются взаимно обратными, то есть:

∀{\displaystyle \forall } допустимых пар открытого и закрытого ключей (p,s){\displaystyle (p,s)}

∃{\displaystyle \exists } соответствующие функции шифрования Ep(x){\displaystyle E_{p}(x)} и расшифрования Ds(x){\displaystyle D_{s}(x)} такие, что

∀{\displaystyle \forall } сообщения m∈M{\displaystyle m\in M}, где M{\displaystyle M} — множество допустимых сообщений,

m=Ds(Ep(m))=Ep(Ds(m)).{\displaystyle m=D_{s}(E_{p}(m))=E_{p}(D_{s}(m)).}

Алгоритм создания открытого и секретного ключей[править | править код]

RSA-ключи генерируются следующим образом:^[16]

1. Выбираются два различных случайных простых числа p{\displaystyle p} и q{\displaystyle q} заданного размера (например, 1024 бита каждое).
2. Вычисляется их произведение n=p⋅q{\displaystyle n=p\cdot q}, которое называется модулем.
3. Вычисляется значение функции Эйлера от числа n{\displaystyle n}:

   φ(n)=(p−1)⋅(q−1).{\displaystyle \varphi (n)=(p-1)\cdot (q-1).}

4. Выбирается целое число e{\displaystyle e} (1<e<φ(n){\displaystyle 1<e<\varphi (n)}), взаимно простое со значением функции φ(n){\displaystyle \varphi (n)}.
   • Число e{\displaystyle e} называется открытой экспонентой (англ. public exponent)
   • Обычно в качестве e{\displaystyle e} берут простые числа, содержащие небольшое количество единичных бит в двоичной записи, например, простые из чисел Ферма: 17, 257 или 65537, так как в этом случае время, необходимое для шифрования с использованием быстрого возведения в степень будет меньше.
   • Слишком малые значения e{\displaystyle e}, например 3, потенциально могут ослабить безопасность схемы RSA.^[17]
5. Вычисляется число d{\displaystyle d}, мультипликативно обратное к числу e{\displaystyle e} по модулю φ(n){\displaystyle \varphi (n)}, то есть число, удовлетворяющее сравнению:

   d⋅e≡1(modφ(n)).{\displaystyle d\cdot e\equiv 1{\pmod {\varphi (n)}}.}

6. Пара (e,n){\displaystyle (e,n)} публикуется в качестве открытого ключа RSA (англ. RSA public key).
7. Пара (d,n){\displaystyle (d,n)} играет роль закрытого ключа RSA (англ. RSA private key) и держится в секрете.

Шифрование и расшифрование[править | править код]

Предположим, Боб хочет послать Алисе сообщение m{\displaystyle m}.

Сообщениями являются целые числа в интервале от 0{\displaystyle 0} до n−1{\displaystyle n-1}, т.е m∈Zn{\displaystyle m\in \mathbb {Z} _{n}}.

Данная схема на практике не используется по причине того, что она не является практически надёжной (semantically secured). Действительно, односторонняя функция E(m) является детерминированной — при одних и тех же значениях входных параметров (ключа и сообщения) выдаёт одинаковый результат. Это значит, что не выполняется необходимое условие практической (семантической) надёжности шифра.

Алгоритм шифрования сеансового ключа[править | править код]

Наиболее используемым в настоящее время является смешанный алгоритм шифрования, в котором сначала шифруется сеансовый ключ, а потом уже с его помощью участники шифруют свои сообщения симметричными системами. После завершения сеанса сеансовый ключ, как правило, уничтожается.

Алгоритм шифрования сеансового ключа выглядит следующим образом^[18]:



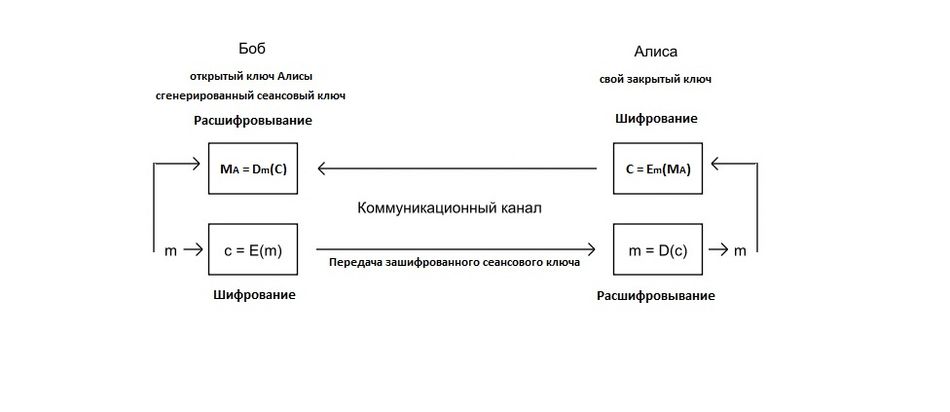
В случае, когда сеансовый ключ больше, чем модуль n{\displaystyle n}, сеансовый ключ разбивают на блоки нужной длины (в случае необходимости дополняют нулями) и шифруют каждый блок.

Корректность схемы RSA[править | править код]

Уравнения (1){\displaystyle (1)} и (2){\displaystyle (2)}, на которых основана схема RSA, определяют взаимно обратные преобразования множества Zn{\displaystyle \mathbb {Z} _{n}}

Пример[править | править код]

Асимметричное шифрование на практике / Habr

Приветствую вас, хабравчане!

Проблемы безопасности — это слабое место большинства из нас. Всем нам неприятно сталкиваться и тем более терять что—то ценное из—за случайного клика мышью. И именно поэтому я решила поделиться найденными материалами с вами.

В стремлении развеять наиболее часто задаваемый вопрос — почему будут атаковать меня? Кому я нужен? — мы начнем статью именно с него.

Нужно учитывать, что атаковать вас может не только человек. Это может делать, например, бот.
Каждый из нас подключен к интернет провайдеру. А на него, скорее всего, происходят атаки буквально каждый день. Замечали у себя на почте раздел «спам»? В каждом таком письме потенциально есть фишинговая атака. Это атака не персонально на вас. Это масштабная атака, ориентированная на широкий круг лиц. Мы потенциально жертвы.

Чаще всего их цель — деньги. Как они могут их получить?

Например, использовать ваш компьютер в качестве web сервера, красть ваш контент, производить email атаки, деятельность в ботнете, кража аккаунтов, атаки с целью вымогательства. Да и email аккаунт — потенциально важная вещь, потому что все мы достаточно часто используем один и тот же пароль на нескольких сервисах.

Время дорого, и мы хотим тратить как можно меньше времени на вопросы, связанные с безопасностью.

И поэтому первое, что нужно сделать — это ответить для себя на несколько вопросов:

• В каких файлах хранятся наиболее важные данные?
• Какие аккаунты в соц сетях вы не можете потерять?
• Что может причинить наибольший вред?
• А что может ударить по вашей репутации?

Ну, например, кража ноутбука. Да, это больно и печально. Но как это может угрожать вам?
Это может быть потеря данных для входа в соц сети. Это может быть конфиденциальная информация, полученная во время работы. А может это личные фотографии.

Окей, мы определились с тем, что нам необходимо защитить. Следующий шаг — выбор метода защиты.

Да, разумеется, в мире существует множество атак и защититься от всех просто невозможно.
Поэтому мы рассмотрим один из наиболее эффективных инструментов — шифрование.

Что такое шифрование?


Чтобы сделать правильный выбор в области безопасности, вам нужно понимать, что такое шифрование. Не обязательно знать хардкорную математику. Достаточно понять на базовом уровне. Это один из лучших и незаменимых инструментов в нашем арсенале.

Шифрование — это метод преобразования данных, пригодных для чтения человеком, в форму, которую человек не сможет прочитать. За счет этого данные остаются конфиденциальными и приватными.

Дешифрование — обратная операция. Преобразование нечитаемых данных в читаемые.

Окей, где это применяется? На самом деле во многих местах. Например, обращали внимание на протокол «https»? Именно за счет него ваши данные не может перехватить 3-й человек во время вашего лазания в интернете. Объясню подробнее. Вы заходите на сайт «www.google.com», делаете любой запрос. При этом все данные, которые необходимы для отображения выдачи результатов, передаются с помощью протокола «https». А значит, если какой-либо человек решит просмотреть данные о вашем трафике (атака Man In the Middle), то он увидит лишь то, что вы зашли на Google. В придачу он получит множество зашифрованных пакетов. То есть можно сказать, что он не получит ничего.

Но вернемся к базовой теории. В процессе шифрования участвуют 2 основных компонента — алгоритм и ключ.

Алгоритм — это в каком-то смысле замок, который позволяет хранить ваши данные в тайне. За счет него происходит преобразование текста.

Ключ — это, уж простите за тавтологию, ключ от замка. Кусочек уникальных данных, с помощью которых происходит преобразование текста

Хм, хорошо. Едем дальше. Слегка повысим напряжение.

Виды шифрования


Как еще мы можем использовать шифрование в своих, корыстных целях? Для простоты понимания мы рассмотрим шифрование архива. При архивации во многих архиваторах присутствует возможность установить пароль. При этом архиватор использует какой-либо алгоритм для шифрования. И чаще всего это симметричный алгоритм.

Симметричное шифрование


Симметричный алгоритм шифрования — алгоритм, при котором для шифрования и дешифрования используется один и тот же ключ. Ярким и, в то же простым примером, будет шифр Цезаря.

Вся работа этого алгоритма заключается в том, чтобы изменить символ на другой с определенным шагом.

Например, при смещении в 5 символов, символ, который стоит на первой позиции заменить на символ 6 позиции и так далее.

Наиболее стойким на данный момент считается алгоритм AES (Advanced Encryption Standard).
Стоит упомянуть еще один момент — мощность пароля. Мощность пароля измеряется в битах. Одним из наиболее распространенных решений является 128 или 256 бит. Это то количество бит, которое будет выделено для пароля. Так же это число означает количество паролей, которое вы можете получить при данном алгоритме шифрования. Но чем больше длина ключа, тем медленнее протекает процесс шифрования или дешифрования.

Но чаще всего используется асимметричное шифрование


И так, мы зашифровали письмо, но как его отправить нашему другу? Отправлять в соц. сетях или текстовым сообщением — не самая лучшая затея. Как и говорить его по телефону.

И это приводит нас к новому типу шифрования.

В ассиметричном шифровании используется 2 ключа — открытый и закрытый(тайный).
Открытый ключ для шифрования, закрытый — для дешифрования.

Какие алгоритмы позволяют пользоваться этой технологией?

Вот списочек:

• Rivest—Shamir—Adleman (RSA) (наиболее распространенный)
• Elliptic curve cryptosystem (ECC)
• Diffie—Hellman (DH)
• El Gamal

Плюсы ассиметричных алгоритмов:
• можно свободно делиться открытым ключом и любой может отправить тебе тайное сообщение.

Минусы:
• скорость шифрования/дешифрования.

Для продвинутыхТак как во мне есть жилка программиста, а также любовь к математике, то я просто не могу не рассказать о том, как все работает «под капотом»

Рассмотрим на примере алгоритма RSA.

Первое, что нам необходимо сделать — сгенерировать открытый и закрытый ключи. Последовательность действий примерно такая:

1) Мы выбираем два простых числа. Желательно, чтобы они были достаточно близкими

p = 19
s = 13

2) Вычисляем их произведение, а также функцию Эйлера

n = p * s
f = (p — 1) * (s — 1)



3) Теперь наиболее затратная по времени часть — выбор экспоненты и произвольного коэффициента.

Дело в том, что при выбранных коэффициентах значение «d» должно быть целым. «d» — необходимая составляющая алгоритма

e = 5
k = 9
d = (k * f + 1)/e

Теперь наш открытый ключ (для шифрования сообщения) состоит из значений переменных «e» и «n», а закрытый ключ (для дешифрования) из значений «d» и «n».
То есть в нашем случае…

Тогда шифрование сообщения происходит по формуле: crypt = m^e%n.
А дешифрование: decrypt = crypt^d%n.

Ну и с точки зрения программиста, мы можем использовать эту информацию следующим образом:

1. Создать массив соответствий символу и его коду (например, ASCII код)
2. Применить алгоритм для каждого символа, создавая массив преобразованных значений
3. Перевести полученный массив обратно в строковый вид
4. Profit!

Как можно использовать асимметричное шифрование для своих целей?

Теперь, зная теорию, плюсы и минусы алгоритма, а также для чего вообще нужно им пользоваться, мы можем говорить о практическом применении.

Среди всех найденных программ, наиболее удобной мне показалась gpg4usb.

Данная программа использует PGP шифрование. Почему я рекомендую использовать именно его?

Все просто. Этот тип шифрования до сих пор еще не удалось взломать. Никому. Так что пользуйтесь.

Пользоваться программой достаточно просто. Нужно лишь знать куда нажимать.
И именно об этом сейчас пойдет речь.

Первое, что необходимо сделать — скачать программу. Вы можете это сделать по ссылке:
ссылка.

Скажу сразу — эта программа кросс—платформенная. То есть вы можете использовать ее как на Windows, так и на Linux.

Второе — это создание пары ключей шифрования.

Это можно сделать, выполнив следующую последовательность действий:

1) Переходим в раздел «Менеджер ключей»

2) Выбираем в верхней панели «Ключ», затем «Генерировать ключ»

Должно выглядеть примерно так:

3) Заполняем необходимые поля. Предупрежу сразу — пароль лучше куда-нибудь записать (или запомнить), потому что он понадобится в последующем для дешифрования сообщения.

Теперь ключ создан, и мы можем приступать непосредственно к шифрованию.

На главном экране присутствует текстовое поле — это наш плацдарм для создания сообщений. В правой боковой панели помечаем галочкой свой ключ.

Введя сообщение в поле, смело нажимаем в верхней панели «Зашифровать».

Поздравляю, вы умеете шифровать сообщения.

Дешифровка происходит аналогично, разве что вместо «Зашифровать» вы пользуетесь кнопкой «Расшифровать».

А теперь момент, который пол часа выносил мне мозг: как передать ключ другу?
Да, мы настроили систему шифрования, и она работает, да, мы можем передать другу открытый ключ и не бояться, что сообщение будет прочитано. Но где его взять?

Как оказалось, все достаточно просто. В окне, в котором мы создавали ключи для шифрования, мы помечаем галочкой нужный ключ и в верхней панели выбираем «Экспорт в файл». Мы получили открытый ключ и можем передавать кому угодно, чтобы получать от него зашифрованные сообщения, которые можем прочитать только мы.

Так, а теперь я хочу получить закрытый ключ (а вдруг буду работать с другого компьютера? Ведь ключи хранятся локально).

Чтобы решить эту задачу, мы вновь возвращаемся на главный экран, в правой боковой панели нажимаем правой кнопкой мыши на нужный ключ и выбираем «Показать свойства ключа». А в открывшемся окне выбираем «Экспортировать Секретный ключ».

Готово, теперь у вас «на руках» открытый и закрытый ключи шифрования, которыми вы можете распоряжаться по своему усмотрению.

Ну и в завершении статьи хочу поделиться полезной методикой: моделирование угроз и оценка рисков.

Первое, что нужно понять — нельзя обеспечить 100% безопасность, как и свести все риски к нулю. Нельзя получить 100% анонимность. Нельзя получить 100% безопасность (разве что не использовать телефон и ПК).

Используя интернет мы так или иначе принимаем риски. Он дает нам шанс расширить свои возможности, но при этом есть риск потери наших данных. Поэтому безопасность — это балансирование между удобством, расширением знаний, комфортом и сохранением уже определенных, важных для нас данных.

Мы должны использовать риск—ориентированный подход.

Риск = уязвимость * угрозы * последствия


Например, кража ноутбука. Что мы можем сделать? Зашифровать весь диск, добавить дополнительные этапы авторизации.

Для обеспечения качественной защиты нужно пройти несколько этапов:

1. Выбираем
2. Настраиваем
3. Оцениваем. Проверяем, что диск зашифрован полностью
4. Контролируем. Проверка обновлений систем безопасности

Криптографическая система с открытым ключом

Криптографическая система с открытым ключом (или Асимметричное шифрование, Асимметричный шифр) — система шифрования и/или электронной цифровой подписи (ЭЦП), при которой открытый ключ передаётся по открытому (то есть незащищённому, доступному для наблюдения) каналу, и используется для проверки ЭЦП и для шифрования сообщения. Для генерации ЭЦП и для расшифрования сообщения используется секретный ключ. ^[1] Криптографические системы с открытым ключом в настоящее время широко применяются в различных сетевых протоколах, в частности, в протоколах SSL (лежащих в основе SSH. Также используется в S/MIME.

Идея криптосистемы с открытым ключом

Идея криптографии с открытым ключом очень тесно связана с идеей односторонних функций, то есть таких функций f(x), что по известному x довольно просто найти значение f(x), тогда как определение x из f(x) сложно в смысле теории.

Но сама односторонняя функция бесполезна в применении: ею можно зашифровать сообщение, но расшифровать нельзя. Поэтому криптография с открытым ключом использует односторонние функции с лазейкой. Лазейка — это некий секрет, который помогает расшифровать. То есть существует такой y, что зная f(x), можно вычислить x. К примеру, если разобрать часы на множество составных частей, то очень сложно собрать вновь работающие часы. Но если есть инструкция по сборке (лазейка), то можно легко решить эту проблему.

Понять идеи и методы криптографии с открытым ключом помогает следующий пример — хранение паролей в компьютере. Каждый пользователь в сети имеет свой пароль. При входе, он указывает имя и вводит секретный пароль. Но если хранить пароль на диске компьютера, то кто-нибудь его может считать (особенно легко это сделать администратору этого компьютера) и получить доступ к секретной информации. Для решения задачи используется односторонняя функция. При создании секретного пароля в компьютере сохраняется не сам пароль, а результат вычисления функции от этого пароля и имени пользователя. Например, пользователь Алиса придумала пароль «Гладиолус». При сохранении этих данных вычисляется результат функции f(АЛИСАГЛАДИОЛУС), пусть результатом будет строка РОМАШКА, которая и будет сохранена в системе. В результате файл паролей примет следующий вид:

Имя	f(имя_пароль)
АЛИСА	РОМАШКА
БОБ	НАРЦИСС

Вход в систему теперь выглядит так:

Имя:	АЛИСА
Пароль:	ГЛАДИОЛУС

Когда Алиса вводит «секретный» пароль, компьютер проверяет, даёт или нет функция, применяемая к АЛИСАГЛАДИОЛУС, правильный результат РОМАШКА, хранящийся на диске компьютера. Стоит изменить хотя бы одну букву в имени или в пароле, и результат функции будет совершенно другим. «Секретный» пароль не хранится в компьютере ни в каком виде. Файл паролей может быть теперь просмотрен другими пользователями без потери секретности, так как функция необратимая.

В предыдущем примере используется односторонняя функция без лазейки, поскольку не требуется по зашифрованному сообщению получить исходное. В следующем примере рассматривается схема с возможностью восстановить исходное сообщение с помощью «лазейки», то есть труднодоступной информации. Для шифрования текста можно взять большой абонентский справочник, состоящий из нескольких толстых томов (по нему очень легко найти номер любого жителя города, но почти невозможно по известному номеру найти абонента). Для каждой буквы из шифруемого сообщения выбирается имя, начинающееся на ту же букву. Таким образом букве ставится в соответствие номер телефона абонента. Отправляемое сообщение, например «КОРОБКА», будет зашифровано следующим образом:

Сообщение	Выбранное имя	Криптотекст
К	Королёв	5643452
О	Орехов	3572651
Р	Рузаева	4673956
O	Осипов	3517289
Б	Батурин	7755628
К	Кирсанова	1235267
А	Арсеньева	8492746

Криптотекстом будет являться цепочка номеров, записанных в порядке их выбора в справочнике. Чтобы затруднить расшифровку, следует выбирать случайные имена, начинающиеся на нужную букву. Таким образом исходное сообщение может быть зашифровано множеством различных списков номеров (криптотекстов).

Примеры таких криптотекстов:

Криптотекст 1	Криптотекст 2	Криптотекст 3
1235267	5643452	1235267
3572651	3517289	3517289
4673956	4673956	4673956
3517289	3572651	3572651
7755628	7755628	7755628
5643452	1235267	5643452
8492746	8492746	8492746

Чтобы расшифровать текст, надо иметь справочник, составленный согласно возрастанию номеров. Этот справочник является лазейкой (секрет, который помогает получить начальный текст), известной только легальным пользователям. Не имея на руках копии справочника, криптоаналитик затратит очень много времени на расшифровку.^[2]

Схема шифрования с открытым ключом

Пусть K — пространство ключей, а e и d — ключи шифрования и расшифрования соответственно. E_e — функция шифрования для произвольного ключа e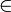K, такая что:

E_e(m) = c

Здесь c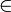C, где C — пространство шифротекстов, а m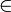M, где M — пространство сообщений.

D_d — функция расшифрования, с помощью которой можно найти исходное сообщение m, зная шифротекст c :

D_d(c) = m

{E_e: e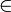K} — набор шифрования, а {D_d: d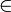K} — соответствующий набор для расшифрования. Каждая пара (E,D) имеет свойство: зная E_e, невозможно решить уравнение E_e(m) = c, то есть для данного произвольного шифротекста c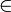C, невозможно найти сообщение m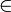M. Это значит, что по данному e невозможно определить соответствующий ключ расшифрования d. E_e является односторонней функцией, а d — лазейкой.^[3]

Ниже показана схема передачи информации лицом А лицу В. Они могут быть как физическими лицами, так и организациями и так далее. Но для более лёгкого восприятия принято участников передачи отождествлять с людьми, чаще всего именуемых Алиса и Боб. Участника, который стремится перехватить и расшифровать сообщения Алисы и Боба, чаще всего называют Евой.


1. Боб выбирает пару (e,d) и шлёт ключ шифрования e (открытый ключ) Алисе по открытому каналу, а ключ расшифрования d (закрытый ключ) защищён и секретен (он не должен передаваться по открытому каналу, либо его подлинность должна быть гарантирована некоторым сертифицирующим органом).
2. Чтобы послать сообщение m Бобу, Алиса применяет функцию шифрования, определённую открытым ключом e: E_e(m) = c, c — полученный шифротекст.
3. Боб расшифровывает шифротекст c, применяя обратное преобразование D_d, однозначно определённое значением d.

Научная основа

Начало асимметричным шифрам было положено в работе «Новые направления в современной криптографии» Уитфилда Диффи и Мартина Хеллмана, опубликованной в 1976 году. Находясь под влиянием работы Ральфа Меркле (Ralph Merkle) о распространении открытого ключа, они предложили метод получения секретных ключей, используя открытый канал. Этот метод экспоненциального обмена ключей, который стал известен как обмен ключами Диффи-Хеллмана, был первым опубликованным практичным методом для установления разделения секретного ключа между заверенными пользователями канала. В 2002 году Хеллман предложил называть данный алгоритм «Диффи — Хеллмана — Меркле», признавая вклад Меркле в изобретение криптографии с открытым ключом. Эта же схема была разработана Малькольмом Вильямсоном в 1970-х, но держалась в секрете до 1997 года. Метод Меркле по распространению открытого ключа был изобретён в 1974 году и опубликован в 1978, его также называют загадкой Меркле.

В 1977 году учёными Рональдом Райвестом (Ronald Linn Rivest), Ади Шамиром (Adi Shamir) и Леонардом Адлеманом (Leonard Adleman) из Массачусетского Технологического Института (MIT) был разработан алгоритм шифрования, основанный на проблеме о разложении на множители. Система была названа по первым буквам их фамилий. Эта же система была изобретена Клиффордом Коксом (Clifford Cocks) в 1973 году, работавшим в центре правительственной связи (GCHQ). Но эта работа хранилась лишь во внутренних документах центра, поэтому о её существовании было не известно до 1977 года.

Вообще, в основу известных асимметричных криптосистем кладётся одна из сложных математических проблем, которая позволяет строить односторонние функции и функции-лазейки. Например, криптосистемы Меркля — Хеллмана и Хора — Ривеста опираются на так называемую задачу об укладке рюкзака.

Основные принципы построения криптосистем с открытым ключом

1. Начинаем с трудной задачи P. Она должна решаться сложно в смысле теории: нет алгоритма, с помощью которого можно было бы перебрать все варианты решения задачи P за полиномиальное время относительно размера задачи.
2. Можно выделить легкую подзадачу P‘ из P. Она должна решаться за полиномиальное время, лучше, если за линейное.
3. «Перетасовываем и взбалтываем» P‘, чтобы получить задачу P», совершенно не похожую на первоначальную. Задача P», по крайней мере, должна выглядеть как оригинальная труднорешаемая задача P.
4. P» открывается с описанием, как она может быть использована в роли ключа зашифрования. Как из P» получить P‘, держится в секрете как секретная лазейка.
5. Криптосистема организована так, что алгоритмы расшифрования для легального пользователя и криптоаналитика существенно различны. В то время как первый решает P» задачу, второй использует секретную лазейку и решает P‘ задачу.

Криптография с несколькими открытыми ключами

• В следующем примере показана схема, в которой Алиса шифрует сообщение так, что только Боб может прочитать его, и наоборот, Боб шифрует сообщение так, что только Алиса может расшифровать его.

Пусть есть 3 ключа K_A, K_B, K_C, распределенные так, как показано в таблице.

Лицо	Ключ
Алиса	KA
Боб	KB
Кэрол	KC
Дэйв	KA, KB
Эллен	KB, KC
Франк	KA, KC

Тогда Алиса может зашифровать сообщение ключом K_A, а Эллен расшифровать ключами K_B, K_C, Кэрол — ключом K_C, а Дэйв расшифровать ключами K_A, K_B. Если Дэйв зашифрует сообщение ключом K_A, то сообщение сможет прочитать Эллен, если ключом K_B, то его сможет прочитать Франк, если же обоими ключами K_A и K_B, то сообщение прочитает Кэрол. По аналогии действуют и другие участники. Таким образом, если используется одно подмножество ключей для шифрования, то для расшифрования требуются оставшиеся ключи множества. Такую схему можно использовать для n ключей.

Шифруется ключом	Расшифровывается ключом
KB и KC	KA
KA и KC	KB
KA и KB	KC
KC	KA, KB
KA	KB, KC
KB	KA, KC

• Теперь можно посылать сообщения группам агентов, не зная заранее состав группы.

Рассмотрим для начала множество, состоящее из трех агентов: Алисы, Боба и Кэрол. Алисе выдаются ключи K_A и K_B, Бобу — K_B и K_C, Кэрол — K_A и K_C. Теперь, если отправляемое сообщение зашифровано ключом K_C, то его сможет прочитать только Алиса, последовательно применяя ключи K_A и K_B. Если нужно отправить сообщение Бобу, сообщение шифруется ключом K_A, Кэрол — ключом K_B. Если нужно отправить сообщение и Алисе и Кэрол, то для шифрования используются ключи K_B и K_C.

Преимущество этой схемы заключается в том, что для её реализации нужно только одно сообщение и n ключей (в схеме с n агентами). Если передаются индивидуальные сообщения, то есть используются отдельные ключи для каждого агента (всего n ключей) и каждого сообщения, то для передачи сообщений всем различным подмножествам требуется 2ⁿ − 2 ключей.

Недостатком такой схемы является то, что необходимо также широковещательно передавать подмножество агентов (список имён может быть внушительным), которым нужно передать сообщение. Иначе каждому из них придется перебирать все комбинации ключей в поисках подходящей. Также агентам придется хранить немалый объём информации о ключах.^[4]

Криптоанализ алгоритмов с открытым ключом

Казалось бы, что криптосистема с открытым ключом — идеальная система, не требующая безопасного канала для передачи ключа шифрования. Это подразумевало бы, что два легальных пользователя могли бы общаться по открытому каналу, не встречаясь, чтобы обменяться ключами. К сожалению, это не так. Рисунок иллюстрирует, как Ева, выполняющая роль активного перехватчика, может захватить систему (расшифровать сообщение, предназначенное Бобу) без взламывания системы шифрования.



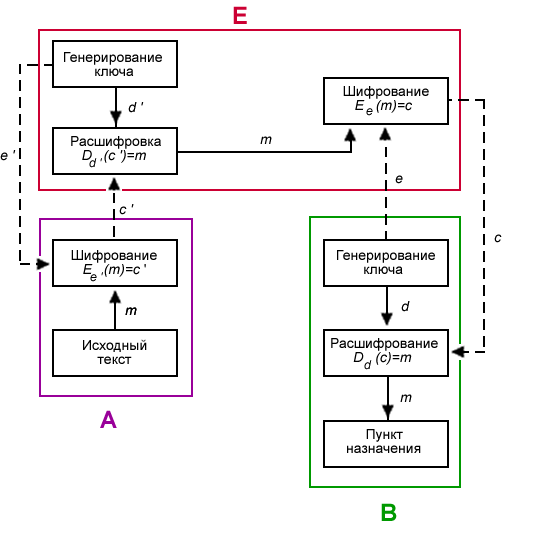
В этой модели Ева перехватывает открытый ключ e, посланный Бобом Алисе. Затем создает пару ключей e’ и d’, «маскируется» под Боба, посылая Алисе открытый ключ e’, который, как думает Алиса, открытый ключ, посланный ей Бобом. Ева перехватывает зашифрованные сообщения от Алисы к Бобу, расшифровывает их с помощью секретного ключа d’, заново зашифровывает открытым ключом e Боба и отправляет сообщение Бобу. Таким образом, никто из участников не догадывается, что есть третье лицо, которое может как просто перехватить сообщение m, так и подменить его на ложное сообщение m‘. Это подчеркивает необходимость аутентификации открытых ключей. Для этого обычно используют сертификаты. Распределённое управление ключами в [5]

Еще одна форма атаки — вычисление закрытого ключа, зная открытый (рисунок ниже). Криптоаналитик знает алгоритм шифрования E_e, анализируя его, пытается найти D_d. Этот процесс упрощается, если криптоаналитик перехватил несколько криптотекстов с, посланных лицом A лицу B.



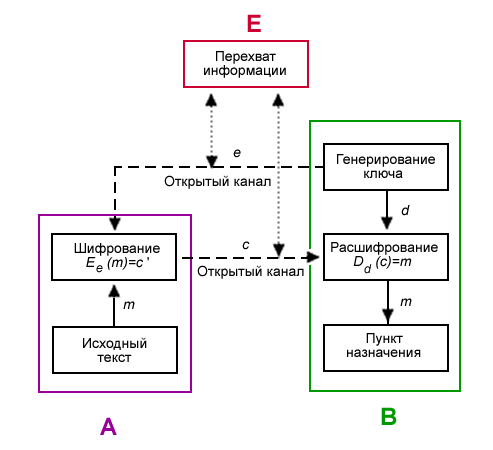
Большинство криптосистем с открытым ключом основаны на проблеме факторизации больших чисел. К примеру,

Год	Число десятичных разрядов в разложенном числе	Во сколько раз сложнее разложить на множители 512-битовое число
1983	71	> 20 000 000
1985	80	> 2 000 000
1988	90	250 000
1989	100	30 000
1993	120	500
1994	129	100

Также задачу разложения потенциально можно решить с помощью Алгоритма Шора при использовании достаточно мощного квантового компьютера.

Для многих методов несимметричного шифрования криптостойкость, полученная в результате криптоанализа, существенно отличается от величин, заявляемых разработчиками алгоритмов на основании теоретических оценок. Поэтому во многих странах вопрос применения алгоритмов шифрования данных находится в поле законодательного регулирования. В частности, в России к использованию в государственных и коммерческих организациях разрешены только те программные средства шифрования данных, которые прошли государственную сертификацию в административных органах, в частности, в ФСБ, ФСТЭК.^[6]

Особенности системы

Применение

Алгоритмы криптосистемы с открытым ключом можно использовать^[7]

• Как самостоятельные средства для защиты передаваемой и хранимой информации
• Как средства распределения ключей. Обычно с помощью алгоритмов криптосистем с открытым ключом распределяют ключи, малые по объёму. А саму передачу больших информационных потоков осуществляют с помощью других алгоритмов.
• Как средства аутентификации пользователей.

Преимущества

• Преимущество асимметричных шифров перед симметричными шифрами состоит в отсутствии необходимости предварительной передачи секретного ключа по надёжному каналу.
• В симметричной криптографии ключ держится в секрете для обеих сторон, а в асимметричной криптосистеме только один секретный.
• При симметричном шифровании необходимо обновлять ключ после каждого факта передачи, тогда как в асимметричных криптосистемах пару (E,D) можно не менять значительное время.
• В больших сетях число ключей в асимметричной криптосистеме значительно меньше, чем в симметричной.

Недостатки

• Преимущество алгоритма симметричного шифрования над несимметричным заключается в том, что в первый относительно легко внести изменения.
• Хотя сообщения надежно шифруются, но «засвечиваются» получатель и отправитель самим фактом пересылки шифрованного сообщения.^[8]
• Несимметричные алгоритмы используют более длинные ключи, чем симметричные. Ниже приведена таблица, сопоставляющая длину ключа симметричного алгоритма с длиной ключа несимметричного алгоритма с аналогичной криптостойкостью:

Длина симметричного ключа, бит	Длина несимметричного ключа, бит
56	384
64	512
80	768
112	1792
128	2304

• Процесс шифрования-расшифрования с использованием пары ключей проходит на два-три порядка медленнее, чем шифрование-расшифрование того же текста симметричным алгоритмом.
• В чистом виде асимметричные криптосистемы требуют существенно больших вычислительных ресурсов, потому на практике используются в сочетании с другими алгоритмами.
  1. Для ЭЦП сообщение предварительно подвергается хешированию, а с помощью асимметричного ключа подписывается лишь относительно небольшой результат хеш-функции.
  2. Для шифрования они используются в форме гибридных криптосистем, где большие объёмы данных шифруются симметричным шифром на сеансовом ключе, а с помощью асимметричного шифра передаётся только сам сеансовый ключ.

Виды симметричных шифров

блочные шифры

потоковые шифры

Виды асимметричных шифров

Примечания

1. ↑ Брюс Шнайер. Прикладная криптография. 2-е изд. Протоколы, алгоритмы и исходные тексты на языке Си. Глава 2.7 Цифровые подписи и шифрование.
2. ↑ Саломаа А. Криптография с открытым ключом. с. 74-75
3. ↑ Handbook of Applied Cryptography, Menezes A.J., Oorschot P.C., Vanstone S.A. С. 25—26
4. ↑ Брюс Шнайер. Прикладная криптография. 2-е изд. Протоколы, алгоритмы и сиходные тексты на языке Си. Глава 3.5
5. ↑ PGP. Распределение ключей..
6. ↑ Принцип достаточной защиты.
7. ↑ Баричев С. Криптография без секретов. с. 20
8. ↑ См. например: Yoshiharu Maeno, Yukio Ohsawa. Discovering covert node in networked organization

См. также

Литература

• Саломаа А. Криптография с открытым ключом. — М.: Мир, 1995. — 318 с. — ISBN 5-03-001991-X
• A. J. Menezes, P. C. van Oorschot, S. A. Vanstone. Handbook of Applied Cryptography. — 1997. — ISBN 0-8493-8523-7
• Шнайер Б. Прикладная криптография. Протоколы, алгоритмы, исходные тексты на языке Си = Applied Cryptography. Protocols, Algorithms and Source Code in C. — М.: Триумф, 2002. — 816 с. — 3000 экз. — ISBN 5-89392-055-4

Wikimedia Foundation. 2010.