Перевод ip адреса в двоичную систему

Теперь, когда мы знаем, что такое IP-адрес, маска подсети, идентификаторы сети и узла, полезно запомнить правила, которые следует применять при назначении этих параметров:

1. идентификатор сети не может содержать только двоичные нули или только единицы. Например, адрес 0.0.0.0 не может являться идентификатором сети;

2. идентификатор узла также не может содержать только двоичные нули или только единицы – такие адреса зарезервированы для специальных целей:

· все нули в идентификаторе узла означают, что этот адрес является адресом сети. Например, 192.168.5.0 является правильным адресом сети при использовании маски 255.255.255.0 и его нельзя использовать для адресации компьютеров,

· все единицы в идентификаторе узла означают, что этот адрес является адресом широковещания для данной сети. Например, 192.168.5.255 является адресом широковещания в сети 192.168.5.0 при использовании маски 255.255.255.0 и его нельзя использовать для адресации компьютеров;

 

3. идентификатор узла в пределах одной и той же подсети должен быть уникальным;

4. диапазон адресов от 127.0.0.1 до 127.255.255.254 нельзя использовать в качестве IP-адресов компьютеров. Вся сеть 127.0.0.0 по маске 255.0.0.0 зарезервирована под так называемый «адрес заглушки» (loopback), используемый в IP для обращения компьютера к самому себе.

Это легко проверить: достаточно на любом компьютере с установленным протоколом TCP/IP выполнить команду

PING 127.12.34.56

и, если протокол TCP/IP работает, вы увидите, как ваш компьютер будет отвечать на собственные запросы.

Классовая и бесклассовая IP-адресация

Первоначальная система IP-адресации в Интернете выглядела следующим образом. Все пространство возможных IP-адресов (а это более четырех миллиардов, точнее 4 294 967 296 адресов) было разбито на пять классов, причем принадлежность IP-адреса к определенному классу определялась по нескольким битам первого октета (табл. 8.2).

Целое (тип данных)

Заметим, что для адресации сетей и узлов использовались только классы A, B и C. Кроме того, для этих сетей были определены фиксированные маски подсети по умолчанию, равные, соответственно, 255.0.0.0, 255.255.0.0 и 255.255.255.0, которые не только жестко определяли диапазон возможных IP-адресов узлов в таких сетях, но и механизм маршрутизации.

Чтобы рассчитать максимально возможное количе-ство узлов в любой IP-сети, достаточно знать, сколько битов содержится в идентификаторе узла, или, иначе, сколько нулей имеется в маске подсети. Это число используется в качестве показателя степени двойки, а затем из результата вычитается два зарезервированных адреса (сети и широковещания). Аналогичным способом легко вычислить и возможное количество сетей классов A, B или C, если учесть, что первые биты в октете уже зарезервированы, а в классе A нельзя использовать IP-адреса 0.0.0.0 и 127.0.0.0 для адресации сети.

Для получения нужного диапазона IP-адресов организациям предлагалось заполнить регистрационную форму, в которой следовало указать текущее число компьютеров и планируемый рост компьютерного парка в течение двух лет.

Первоначально данная схема хорошо работала, поскольку количество сетей было небольшим. Однако с развитием Интернета такой подход к распределению IP-адресов стал вызывать проблемы, особенно острые для сетей класса B. Действительно, организациям, в которых число компьютеров не превышало нескольких сотен (скажем, 500), приходилось регистрировать для себя целую сеть класса B. Поэтому количество доступных сетей класса B стало на глазах «таять», но при этом громадные диапазоны IP-адресов (в нашем примере – более 65000) пропадали зря.

Чтобы решить проблему, была разработана бесклассовая схема IP-адресации (Classless InterDomain Routing, CIDR), в которой не только отсутствует привязка IP-адреса к классу сети и маске подсети по умолчанию, но и допускается применение так называемых

масок подсети с переменной длиной (Variable Length Subnet Mask, VLSM). Например, если при выделении сети для вышеуказанной организации с 500 компьютерами вместо фиксированной маски 255.255.0.0 использовать маску 255.255.254.0,то получившегося диапазона из 512 возможных IP-адресов будет вполне достаточно.

Оставшиеся 65 тысяч адресов можно зарезервировать на будущее или раздать другим желающим подключиться к Интернету.

Этот подход позволил гораздо более эффективно выделять организациям нужные им диапазоны IP-адресов, и проблема с нехваткой IP-сетей и адресов стала менее острой.

Дата добавления: 2014-11-25; Просмотров: 1686; Нарушение авторских прав?;

Системы счисления, преобразование систем счисления, примеры перевода систем счисления

В мире существует много разных систем счисления: десятичная, двоичная, восьмеричная, двенадцатеричная, двадцатеричная, шестнадцатеричная, шестидесятеричная и др.

Каждую систему счисления мы разбирать не будем, так как нам это не пригодится, гораздо важнее разобраться в двух системах счисления для решения любых сетевых задач: десятичной и двоичной, я называю их «системами счисления в IP».

Для успешной сдачи тестов, экзаменов, контрольных и прочих работ, вам также потребуется знать о восьмеричной и шестнадцатеричной системе счисления. С ними гораздо легче будет разобраться, если вы овладеете двоичной системой счисления.

Итак, разбираемся в первых двух.

Системы счисления в ip

При делении сетей на подсети мы часто будет переводить ip адрес и маску из десятичной системы счисления в двоичную, и обратно. Именно поэтому я их назвал системами счисления ip.

Давайте скорее познакомимся с ними, научимся преобразовывать между собой и посмотрим много простых и понятных примеров.

Десятичная система счисления

Десятичная система счисления известна всем нам очень подробно, мы ею пользуемся каждый день (при оплате за транспорт, подсчёте количества штук чего либо, арифметические операции над числами). В десятичную систему счисления входят 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

Десятичная система счисления является позиционной системой, потому что зависит от того, в каком месте числа (в каком разряде, на какой позиции) стоит цифра. Т.е. 001 – единица, 010 – это уже десять, 100 – а это сто. Мы видим, что менялась только позиция одной цифры (единицы), а число менялось очень значительно.

В любой позиционной системе счисления позиция цифры представляет собой цифру, помноженную на число основания системы счисления в степени позиции этой цифры. Посмотрите на пример, и станет всё ясно.

Число десятичное 123 = (1 * 10^2) + (2 * 10^1) + (3 * 10^0) = (1*100) + (2*10) + (3*1)

Число десятичное 209 = (2 * 10^2) + (0 * 10^1) + (9 * 10^0) = (2*100) + (0*10) + (9*1)

Двоичная система счисления

Двоичная система счисления нам может быть и вовсе не знакома, но поверьте, она намного проще, чем привычная нам десятичная система. В двоичную систему счисления входят всего 2 цифры: 0 и 1. Это сравнимо с лампочкой, когда она не горит – это 0, а когда свет включен – это 1.

Двоичная система счисления, как и десятичная, является позиционной.

Число двоичное 1111 = (1*2^3) + (1*2^2) + (1*2^1) + (1*2^0) = (1*8) + (1*4) + (1*2) + (1*1) = 8 + 4 + 2 + 1 = 15 (десятичное).

Число двоичное 0000 = (0*2^3) + (0*2^2) + (0*2^1) + (0*2^0) = (0*8) + (0*4) + (0*2) + (0*1) = 8 + 4 + 2 + 1 = 0 (десятичное).

Хотели мы того, или нет, но мы уже преобразовали 2 двоичных числа в десятичные. Рассмотрим более подробно дальше.

Из двоичной в десятичную систему счисления

Из двоичной системы счисления в десятичную систему счисления переводить не сложно, надо выучить степени двойки от 0 до 15, хотя в большинстве случаев будет достаточным от 0 до 7. Это связано с восемью битами каждого октета в ip адресе.

Для преобразования двоичного числа надо будет каждую цифру помножить на число 2 (основание системы счисления) в степени позиции той цифры, а затем сложить те цифры. В примерах ниже всё будет ясно.

Начнем с простых чисел и закончим числами из восьми цифр.

Число двоичное 111 = (1*2^2) + (1*2^1) + (1*2^0) = (1*4) + (1*2) + (1*1) = 4 + 2 + 1 = 7 (десятичное).

Число двоичное 001 = (0*2^2) + (0*2^1) + (1*2^0) = (0*4) + (0*2) + (1*1) = 0 + 0 + 1 = 1 (десятичное).

Число двоичное 100 = (1*2^2) + (0*2^1) + (0*2^0) = (1*4) + (0*2) + (0*1) = 4 + 0 + 0 = 4 (десятичное).

Число двоичное 101 = (1*2^2) + (0*2^1) + (1*2^0) = (1*4) + (0*2) + (1*1) = 4 + 0 + 1 = 5 (десятичное).

Точно таким же образом можно преобразовать любое двоичное число в десятичное.

Число двоичное 1010 = (1*2^3) + (0*2^2) + (1*2^1) + (0*2^0) = (1*8) + (0*4) + (1*2) + (0*1) = 8 + 0 + 2 + 0 = 10 (десятичное).

Число двоичное 10000001 = (1*2^7) + (0*2^6) + (0*2^5) + (0*2^4) + (0*2^3) + (0*2^2) + (0*2^1) + (1*2^0) = (1*128) + (0*64) + (0*32) + (0*16) + (0*8) + (0*4) + (0*2) + (1*1) = 128 + 0 + 0 + 0 + 0 + 0 + 0 + 1 = 129 (десятичное).

А так же когда вам надоест считать действия с нулями, то пропускайте их. Ваши подсчёты станут краткими и красивыми.

Число двоичное 10000001 = (1*2^7) + (1*2^0) = (1*128) + (1*1) = 128 + 1 = 129 (десятичное).

Число двоичное 10000011 = (1*2^7) + (1*2^1) + (1*2^0) = (1*128) + (1*2) + (1*1) = 128 + 2 + 1 = 131 (десятичное).

Число двоичное 01111111 = (1*2^6) + (1*2^5) + (1*2^4) + (1*2^3) + (1*2^2) + (1*2^1) + (1*2^0) = (1*64) + (1*32) + (1*16) + (1*8) + (1*4) + (1*2) + (1*1) = 64 + 32 + 16 + 8 + 4 + 2 + 1 = 127 (десятичное).

Число двоичное 11111111 = (1*2^7) + (1*2^6) + (1*2^5) + (1*2^4) + (1*2^3) + (1*2^2) + (1*2^1) + (1*2^0) = (1*128) + (1*64) + (1*32) + (1*16) + (1*8) + (1*4) + (1*2) + (1*1) = 128 + 64 + 32 + 16 + 8 + 4 + 2 + 1 = 255 (десятичное).

Число двоичное 01111011 = (1*2^6) + (1*2^5) + (1*2^4) + (1*2^3) + (1*2^1) + (1*2^0) = (1*64) + (1*32) + (1*16) + (1*8) + (1*2) + (1*1) = 64 + 32 + 16 + 8 + 2 + 1 = 123 (десятичное).

Число двоичное 11010001 = (1*2^7) + (1*2^6) + (1*2^4) + (1*2^0) = (1*128) + (1*64) + (1*16) + (1*1) = 128 + 64 + 16 + 1 = 209 (десятичное).

Вот и справились. Теперь переведём всё обратно из двоичной в десятичную.

Из десятичной в двоичную систему счисления

Перевод из десятичной системы счисления в двоичную систему тоже не труден, только вместо сложения потребуется вычитание.

Последовательность перевода в десятичную систему счисления следующая: надо вычесть из переводимого числа ближайшее (меньшее или равное) число к нему из степеней двойки. Затем проделать тоже самое с получившимся значением, и так до нуля. В зависимости от используемой степени двойки записать цифру 1 в нужном разряде двоичного числа, пропуски заполнить единицами.

Смотрите примеры, и вопросы отпадут сами собой.

Число десятичное 7: 7-4=3 — ближайшее меньшее (или равное) число к 7 из степеней двойки это 4 (2^2). Вычитаем из 7 число 4, получаем 3. Затем 3-2=1 — ближайшее меньшее (или равное) число к 3 из степеней двойки это 2 (2^1). Вычитаем из 3 число 2, получаем 1. 1-1=0 — ближайшее меньшее (или равное) число к 1 из степеней двойки это 1 (2^0). Вычитаем из 1 число 1, получаем 0. Всего из нашего числа мы вычли 4, 2 и 1, т.е. 2^2, 2^1 и 2^0. Ставим единицы в разряды по степеням двоек – 111. Если мы считаем октетом, то надо добавить нули – 00000111. Готово.

Чтобы не сбивать вас, уберём слова:

Число десятичное 10: 10-8=2; 2-2=0. Двоичное число – 00001010.

Число десятичное 129: 129-128=1; 1-1=0. Двоичное число – 10000001.

Число десятичное 131: 131-128=3; 3-2=1; 1-1=0. Двоичное число – 10000011.

Число десятичное 127: 127-64=63; 63-32=31; 31-16=15; 15-8=7; 7-4=3; 3-2=1; 1-1=0. Двоичное число – 01111111.

Число десятичное 255: 255-128=127; 127-64=63; 63-32=31; 31-16=15; 15-8=7; 7-4=3; 3-2=1; 1-1=0. Двоичное число – 11111111.

Число десятичное 123: 123-64=59; 59-32=27; 27-16=11; 11-8=3; 3-2=1; 1-1=0. Двоичное число – 01111011.

Число десятичное 209: 209-128=81; 81-64=17; 17-16=1; 1-1=0. Двоичное число – 11010001.

Заключение

Как вы видите, переводить из двоичной системы счисления в десятичную систему счисления не очень сложно. Это преобразование мы будет часто использовать при делении сетей на подсети.

Попробуйте сами преобразовать ваши число и год рождения. Для проверки можете использовать виндовс-калькулятор в инженерном режиме или режиме Программист.

Уделите несколько минут для «систем счисления в ip» — двоичной и десятичной.

Двоичное преобразование адресов TCP/IP | Энциклопедия Windows

В двоичной системе исчисления используется только две цифры: 0 и 1. Так как это система исчисления с основанием, равным 2, то каждая позиция в двоичной последовательности представляет степень двойки. Если связать это со стандартной десятичной системой исчисления, которая используется каждый день, то можно понять, что все не так плохо.

Возьмем число 201. При рассмотрении этого трехзначного числа можно заметить, что в нем присутствует разряд единиц, разряд десятков и разряд сотен. Поэтому число 201 равно 1х1+0х10+2х100. Цифра в каждом разряде умножается на степень 10 с показателем, соответствующим положению разряда. Так как двоичная система исчисления имеет основание 2, цифра каждого разряда умножается на степень двойки, соответствующую положению разряда.

Для преобразования десятичных чисел в двоичное представление, можно просто начать с единицы и продолжить удвоение числа, пока не будет достигнуто значение 128. После этого необходимо использовать последовательность нумерации из приведенной таблицы преобразования.

Теперь посмотрим, как адрес IP 10.8.32.6 преобразовывается в двоичную форму.

Использование простой таблицы для преобразования двоичных чисел

Столбцы двоичных разрядов (по основанию 2)
Десятичное число	128	64	32	16	8	4	2	1
10	0	0	0	0	1	0	1	0
8	0	0	0	0	1	0	0	0
32	0	0	1	0	0	0	0	0
6	0	0	0	0	0	1	1	0

Вот пример техники для преобразования десятичного числа в двоичное представление.

1. Найдите наибольшее число в таблице преобразования, которое меньше или равно числу, преобразование которого необходимо выполнить (128, 64, 32, 8 и т.д.) и укажите 1 в его столбце.

2. Отнимите число из выбранной колонки от числа, преобразование которого выполняется.

3. Найдите наибольшее число в таблице преобразования, которое меньше или равно числу, оставшемуся после первого шага, и поместите 1 в столбец этого числа.

4. Отнимите число из выбранного столбца от числа, которое осталось на шаге 2.

5. Повторите шаги 3 и 4, пока разность не станет равна 0; после этого поместите 0 во все столбцы, которые не содержат 1. Вот это и будет наше двоичное число!

Для преобразования числа 10 необходимо найти в таблице самое большое число, не превышающее 10. Это будет 8, поэтому в столбец числа 8 необходимо поместить 1. После этого необходимо отнять 8 от 10. В результате получится число 2. В столбце, соответствующем числу 2, необходимо разместить 1. Результатом последней разности будет 2, поэтому для завершения преобразования во все остальные столбцы необходимо поместить 0.

Использование этой таблицы для преобразования двоичного числа в десятичное еще проще, чем преобразование десятичного числа в двоичное. Просто запишите 8-разрядное число в таблице, указывая каждый разряд в одном столбце таблицы. После этого сложите значения столбцов таблицы, которые содержат 1. Например, двоичное число 10100001 будет равно 128+32+1 или 161.

В главе 4 будет показано, как использовать бесплатную утилиту, предоставленную на сопровождающем компакт-диске, для преобразования адресов IP в разные представления. Поэтому не будем больше тратить время на двоичную арифметику и сразу перейдем к структуре адреса TCP/IP.

Двоичная форма записи ip-адресов

Наряду с традиционной десятичной формой записи IP-адресов, может использоваться и двоичная форма, отражающая непосредственно способ представления адреса в памяти компьютера. Поскольку IP-адрес имеет длину 4 байта, то в двоичной форме он представляется как 32-разрядное двоичное число (т.е. последовательность из 32 нулей и единиц). Например, адрес 213.128.193.154 в двоичной форме имеет вид 11010101 1000000 11000001 10011010. Используя двоичную форму записи IP-адреса, легко определить схемы классов IP адресов:

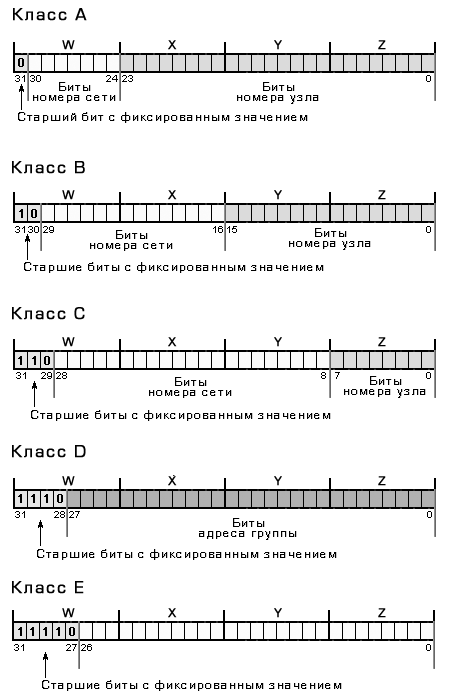
Двоичные схемы IP-адресов классов A, B, C, D и E

 

Особые ip-адреса

Протокол IP предполагает наличие адресов, которые трактуются особым образом. К ним относятся следующие:

1. Адреса, значение первого октета которых равно 127. Пакеты, направленные по такому адресу, реально не передаются в сеть, а обрабатываются программным обеспечением узла-отправителя. Таким образом, узел может направить данные самому себе. Этот подход очень удобен для тестирования сетевого программного обеспечения в условиях, когда нет возможности подключиться к сети.

2. Адрес 255.255.255.255. Пакет, в назначении которого стоит адрес 255.255.255.255, должен рассылаться всем узлам сети, в которой находится источник. Такой вид рассылки называется ограниченным широковещанием. В двоичной форме этот адрес имеет вид 11111111 11111111 11111111 11111111.

3. Адрес 0.0.0.0. Он используется в служебных целях и трактуется как адрес того узла, который сгенерировал пакет. Двоичное представление этого адреса 00000000 00000000 00000000 00000000

 Дополнительно особым образом интерпретируются адреса:

1. содержащие 0 во всех двоичных разрядах поля номера узла; такие IP-адреса используются для записи адресов сетей в целом;

2. содержащие 1 во всех двоичных разрядах поля номера узла; такие IP-адреса являются широковещательными адресами для сетей, номера которых определяются этими адресами.

Использование масок для ip-адресации

Схема разделения IP-адреса на номер сети и номер узла, основанная на понятии класса адреса, является достаточно грубой, поскольку предполагает всего 3 варианта (классы A, B и C) распределения разрядов адреса под соответствующие номера. Рассмотрим для примера следующую ситуацию. Допустим, что некоторая компания, подключающаяся к Интернет, располагает всего 10-ю компьютерами. Поскольку минимальными по возможному числу узлов являются сети класса C, то эта компания должна была бы получить от организации, занимающейся распределением IP-адресов, диапазон в 254 адреса (одну сеть класса C). Неудобство такого подхода очевидно: 244 адреса останутся неиспользованными, поскольку не могут быть распределены компьютерам других организаций, расположенных в других физических сетях. В случае же, если рассматриваемая организация имела бы 20 компьютеров, распределенных по двум физическим сетям, то ей должен был бы выделяться диапазон двух сетей класса C (по одному для каждой физической сети). При этом число «мертвых» адресов удвоится.

Для более гибкого определения границ между разрядами номеров сети и узла внутри IP-адреса используются так называемые маски подсети. Маска подсети – это 4-байтовое число специального вида, которое используется совместно с IP-адресом. «Специальный вид» маски подсети заключается в следующем: двоичные разряды маски, соответствующие разрядам IP-адреса, отведенным под номер сети, содержат единицы, а в разрядах, соответствующих разрядам номера узла – нули.

Маска подсети обязательно указывается при настройке программного модуля протокола IP на каждом компьютере вместе с IP-адресом. Использование в паре с IP -адресом маски подсети позволяет отказаться от применения классов адресов и сделать более гибкой всю систему IP-адресации. Так, например, маска 255.255.255.240 (11111111 11111111 11111111 11110000) позволяет разбить диапазон в 254 IP-адреса, относящихся к одной сети класса C, на 14 диапазонов, которые могут выделяться разным сетям.

Для стандартного деления IP-адресов на номер сети и номер узла, определенного классами A, B и C маски подсети имеют вид:

Класс	Двоичная форма	Десятичная форма
A	11111111 00000000 00000000 00000000	255.0.0.0
В	11111111 11111111 00000000 00000000	255.255.0.0
С	11111111 11111111 11111111 00000000	255.255.255.0

11010001 00101111 10001111 01010000 .

Двоичный адрес и так в двоичной форме

Может, в десятичной, а не двоичной? Потому что он и так в двоичной форме.. . Итак, открываем Калькулятор в Windows 7, выбираем «Вид -> Программист». Вписываем каждую серию цифр (каждые 8 цифр) в виде BIN и переводим в DEC. Получаем 209.47.143.80

Двоичный адрес в двоичной форме? Он же уже по определению двоичный: ) Обыкновенным образом записанный адрес (т. е. в десятичной форме) перевести в двоичный формат можно следующим образом: Например: 192. 168. 0. 2 Запускаете калькулятор (стандартное виндовское приложение) . Переводите в режим «Программист» (для Windows 7) или «Advanced» для более старых версий (это делается через меню Вид/View. Пишете цифру 192, потом переключаете в положение Bin (двоичные цифры) . Видите тоже число в двоичной системе счисления. Записывате его. Тоже самое повторяете для всех цифр, в нашем случае — 168, 0, 2. Всё. Верно и обратное — если хотите перевести из двоичного вида в десятеричный — то сначала переводите в режим BIN, набираете цифры (только нули и еденицы) , а потом кликаете DEC и смотрите что получилось.

Мож в десятичной форме? Если в десятичной то можно тупо на калькуляторе перевести. Открываешь Вид-Инженерный. Тыкаешь на Bin вставляешь свою десятиную запись и тыкаешь Dec . вот что получится: 209.47.143.80

Перевод Десятичного числа в Двоичное

Мало того, что мы должны быть в состоянии преобразовать двоичное число в десятичное, мы также должны уметь переводить десятичное число в двоичное. Часто приходиться исследовать отдельный октет адреса, который дается в десятичном представлении с разделительными точками. Например, это необходимо, когда сетевые биты и хостовые биты делят октет.

К примеру, если бы узел с 172.16.4.20 использовал 28 битов для сетевого адреса, мы должны были бы исследовать двоичное число в последнем октете, чтобы определить, что этот узел находится в сети 172.16.4.16. Этот процесс извлечения сетевого адреса из полного адреса узла будет объяснен позже.

Значения адреса Между 0 и 255

Поскольку наше представление адресов ограничивается десятичными значениями для одного октета, мы исследуем только процесс преобразования 8-разрядного двоичного числа к десятичным значениям от 0 до 255.

Чтобы начать процесс преобразования, мы начинаем с определения, равно ли или больше десятичное число чем самое большое десятичное значение, представляемое старшим значащим битом. В самой старшей позиции (или 128-разрядной позиции, поскольку 2^7=128) мы определяем, равно ли или больше значение чем 128. Если значение меньше чем 128, мы помещаем 0 в 128-разрядную позицию и переходим к 64-разрядной позиции.

Если значение больше или равно 128, мы помещаем 1 в 128-разрядную позицию и вычитаем 128 из преобразовываемого числа. Затем сравниваем остаток от этой операции со следующим меньшим значением, т.е. 64. Мы продолжаем этот процесс для всех оставшихся позиций.

См. рисунок, на котором изображен пример этих шагов. Мы преобразовываем 172 в 10101100.

Смотрите шаги преобразования, чтобы увидеть, как IP-адрес преобразовывается в двоичное число.

---

Итоги по Преобразованиям

Рисунок подводит итог полного преобразования 172.16.4.20 из десятичного представления с разделительными точками в двоичную запись.

Далее: Типы IP Адресов

Смотрите также

Написать

Перевод чисел из одной системы счисления в другую онлайн

С помощю этого онлайн калькулятора можно перевести целые и дробные числа из одной системы счисления в другую. Дается подробное решение с пояснениями. Для перевода введите исходное число, задайте основание сисемы счисления исходного числа, задайте основание системы счисления, в которую нужно перевести число и нажмите на кнопку «Перевести». Теоретическую часть и численные примеры смотрите ниже.

 Результат уже получен!

Перевод целых и дробных чисел из одной системы счисления в любую другую − теория, примеры и решения

Существуют позиционные и не позиционные системы счисления. Арабская система счисления, которым мы пользуемся в повседневной жизни, является позиционной, а римская − нет. В позиционных системах счисления позиция числа однозначно определяет величину числа. Рассмотрим это на примере числа 6372 в десятичном системе счисления. Пронумеруем это число справа налево начиная с нуля:

число	6	3	7	2
позиция	3	2	1	0

Тогда число 6372 можно представить в следующем виде:

6372=6000+300+70+2 =6·10³+3·10²+7·10¹+2·10⁰.

Число 10 определяет систему счисления (в данном случае это 10). В качестве степеней взяты значения позиции данного числа.

Рассмотрим вещественное десятичное число 1287.923. Пронумеруем его начиная с нуля позиции числа от десятичной точки влево и вправо:

число	1	2	8	7	.	9	2	3
позиция	3	2	1	0		-1	-2	-3

Тогда число 1287.923 можно представить в виде:

1287.923 =1000+200+80 +7+0.9+0.02+0.003 = 1·10³ +2·10² +8·10¹+7·10⁰+9·10^-1+2·10^-2+3·10^-3.

В общем случае формулу можно представить в следующем виде:

Ц_n·sⁿ+Ц_n-1·s^n-1+…+Ц₁·s¹+Ц₀·s⁰+Д_-1·s^-1+Д_-2·s^-2+…+Д_-k·s^-k

(1)

где Ц_n-целое число в позиции n, Д_-k— дробное число в позиции (-k), s — система счисления.

Несколько слов о системах счисления.Число в десятичной системе счисления состоит из множества цифр {0,1,2,3,4,5,6,7,8,9}, в восьмеричной системе счисления — из множества цифр {0,1,2,3,4,5,6,7}, в двоичной системе счисления — из множества цифр {0,1}, в шестнадцатеричной системе счисления — из множества цифр {0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F}, где A,B,C,D,E,F соответствуют числам 10,11,12,13,14,15.

В таблице Таб.1 представлены числа в разных системах счисления.

Таблица 1
Система счисления
10	2	8	16
0	0	0	0
1	1	1	1
2	10	2	2
3	11	3	3
4	100	4	4
5	101	5	5
6	110	6	6
7	111	7	7
8	1000	10	8
9	1001	11	9
10	1010	12	A
11	1011	13	B
12	1100	14	C
13	1101	15	D
14	1110	16	E
15	1111	17	F

 

Перевод чисел из одной системы счисления в другую

Для перевода чисел с одной системы счисления в другую, проще всего сначала перевести число в десятичную систему счисления, а затем, из десятичной системы счисления перевести в требуемую систему счисления.

Перевод чисел из любой системы счисления в десятичную систему счисления

С помощью формулы (1) можно перевести числа из любой системы счисления в десятичную систему счисления.

Пример 1. Переводить число 1011101.001 из двоичной системы счисления (СС) в десятичную СС. Решение:

1·2⁶+0·2⁵+1·2⁴+1·2³+1·2² +0·2¹+1·2⁰+0·2^-1+0·2^-2+1·2^-3 =64+16+8+4+1+1/8=93.125

Пример 2. Переводить число 1011101.001 из восьмеричной системы счисления (СС) в десятичную СС. Решение:

Пример 3. Переводить число AB572.CDF из шестнадцатеричной системы счисления в десятичную СС. Решение:

Здесь A -заменен на 10, B — на 11, C— на 12, F — на 15.

Перевод чисел из десятичной системы счисления в другую систему счисления

Для перевода чисел из десятичной системы счисления в другую систему счисления нужно переводить отдельно целую часть числа и дробную часть числа.

Целую часть числа переводится из десятичной СС в другую систему счисления — последовательным делением целой части числа на основание системы счисления (для двоичной СС — на 2, для 8-ичной СС — на 8, для 16-ичной — на 16 и т.д.) до получения целого остатка, меньше, чем основание СС.

Пример 4. Переведем число 159 из десятичной СС в двоичную СС:

159	2
158	79	2
1	78	39	2
	1	38	19	2
		1	18	9	2
			1	8	4	2
				1	4	2	2
					0	2	1
						0

Рис. 1

Как видно из Рис. 1, число 159 при делении на 2 дает частное 79 и остаток 1. Далее число 79 при делении на 2 дает частное 39 и остаток 1 и т.д. В результате построив число из остатков деления (справа налево) получим число в двоичной СС: 10011111. Следовательно можно записать:

159₁₀=10011111₂.

Пример 5. Переведем число 615 из десятичной СС в восьмеричную СС.

615	8
608	76	8
7	72	9	8
	4	8	1
		1

Рис. 2

При приведении числа из десятичной СС в восьмеричную СС, нужно последовательно делить число на 8, пока не получится целый остаток меньшее, чем 8. В результате построив число из остатков деления (справа налево) получим число в восьмеричной СС: 1147(см. Рис. 2). Следовательно можно записать:

615₁₀=1147₈.

Пример 6. Переведем число 19673 из десятичной системы счисления в шестнадцатеричную СС.

19673	16
19664	1229	16
9	1216	76	16
	13	64	4
		12

Рис. 3

Как видно из рисунка Рис.3, последовательным делением числа 19673 на 16 получили остатки 4, 12, 13, 9. В шестнадцатеричной системе счисления числе 12 соответствует С, числе 13 — D. Следовательно наше шестнадцатеричное число — это 4CD9.

Далее рассмотрим перевод правильных десятичных дробей в двоичную СС, в восьмеричную СС, в шестнадцатеричную СС и т.д.

Для перевода правильных десятичных дробей (вещественное число с нулевой целой частью) в систему счисления с основанием s необходимо данное число последовательно умножить на s до тех пор, пока в дробной части не получится чистый нуль, или же не получим требуемое количество разрядов. Если при умножении получится число с целой частью, отличное от нуля, то эту целую часть не учитывать (они последовательно зачисливаются в результат).

Рассмотрим вышеизложенное на примерах.

Пример 7. Переведем число 0.214 из десятичной системы счисления в двоичную СС.

		0.214
	x	2
0		0.428
	x	2
0		0.856
	x	2
1		0.712
	x	2
1		0.424
	x	2
0		0.848
	x	2
1		0.696
	x	2
1		0.392

Рис. 4

Как видно из Рис.4, число 0.214 последовательно умножается на 2. Если в результате умножения получится число с целой частью, отличное от нуля, то целая часть записывается отдельно (слева от числа), а число записывается с нулевой целой частью. Если же при умножении получиться число с нулевой целой частью, то слева от нее записывается нуль. Процесс умножения продолжается до тех пор, пока в дробной части не получится чистый нуль или же не получим требуемое количество разрядов. Записывая жирные числа (Рис.4) сверху вниз получим требуемое число в двоичной системе счисления: 0.0011011.

Следовательно можно записать:

0.214₁₀=0.0011011₂.

Пример 8. Переведем число 0.125 из десятичной системы счисления в двоичную СС.

		0.125
	x	2
0		0.25
	x	2
0		0.5
	x	2
1		0.0

Рис. 5

Для приведения числа 0.125 из десятичной СС в двоичную, данное число последовательно умножается на 2. В третьем этапе получилось 0. Следовательно, получился следующий результат:

0.125₁₀=0.001₂.

Пример 9. Переведем число 0.214 из десятичной системы счисления в шестнадцатеричную СС.

		0.214
	x	16
3		0.424
	x	16
6		0.784
	x	16
12		0.544
	x	16
8		0.704
	x	16
11		0.264
	x	16
4		0.224

Рис. 6

Следуя примерам 4 и 5 получаем числа 3, 6, 12, 8, 11, 4. Но в шестнадцатеричной СС числам 12 и 11 соответствуют числа C и B. Следовательно имеем:

0.214₁₀=0.36C8B4₁₆.

Пример 10. Переведем число 0.512 из десятичной системы счисления в восьмеричную СС.

		0.512
	x	8
4		0.096
	x	8
0		0.768
	x	8
6		0.144
	x	8
1		0.152
	x	8
1		0.216
	x	8
1		0.728

Рис. 7

Получили:

0.512₁₀=0.406111₈.

Пример 11. Переведем число 159.125 из десятичной системы счисления в двоичную СС. Для этого переведем отдельно целую часть числа (Пример 4) и дробную часть числа (Пример 8). Далее объединяя эти результаты получим:

159.125₁₀=10011111.001₂.

Пример 12. Переведем число 19673.214 из десятичной системы счисления в шестнадцатеричную СС. Для этого переведем отдельно целую часть числа (Пример 6) и дробную часть числа (Пример 9). Далее объединяя эти результаты получим:

19673.214₁₀=4CD9.36C8B4₁₆.