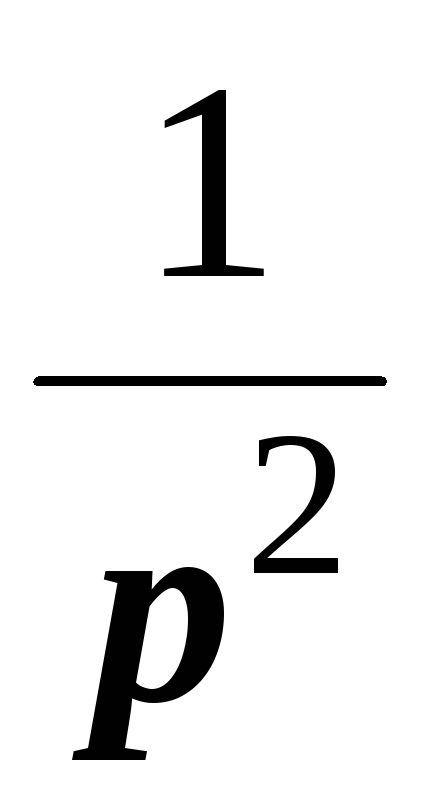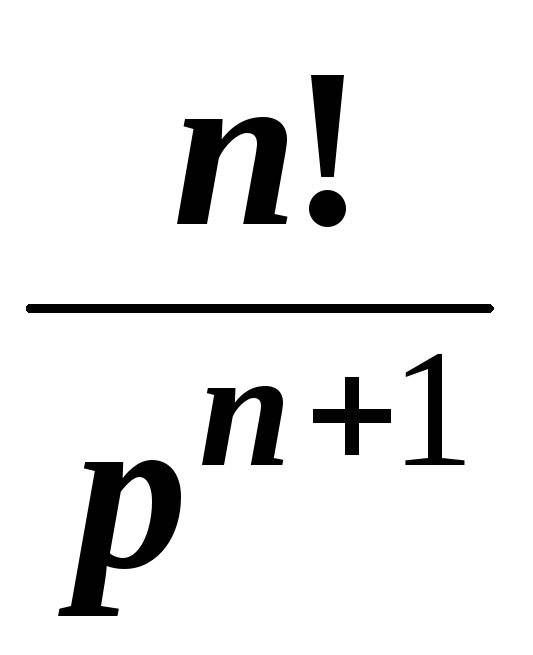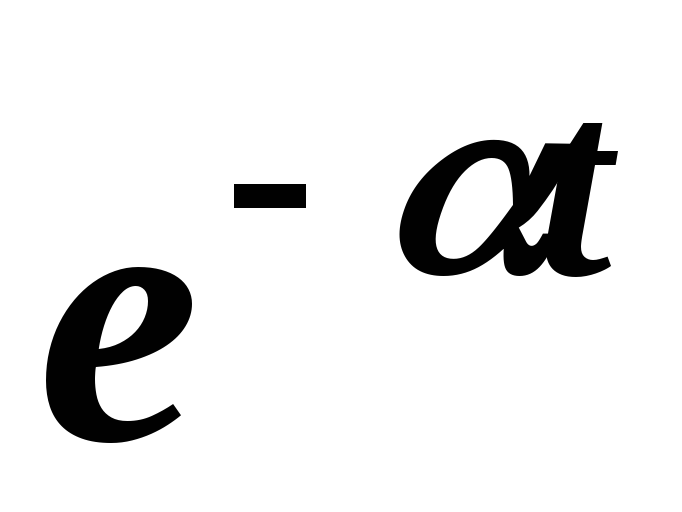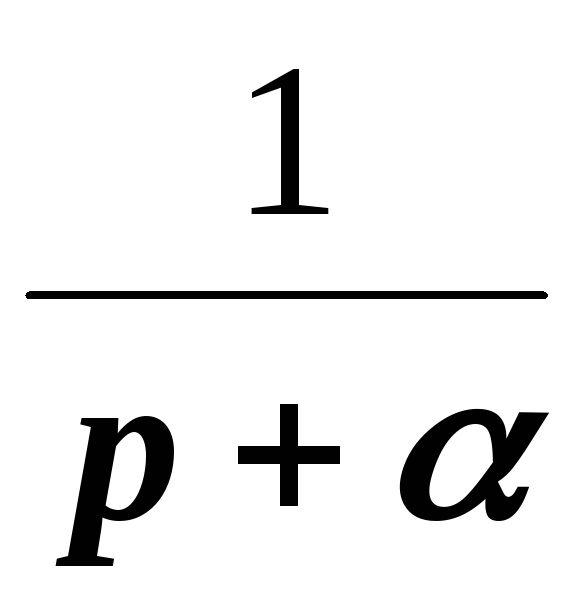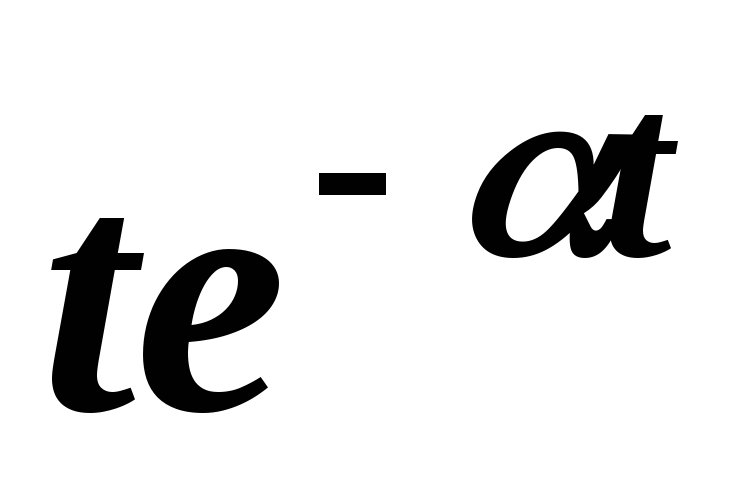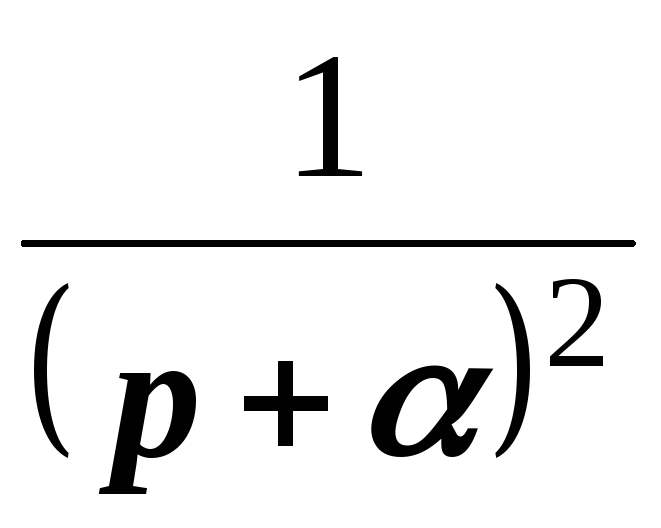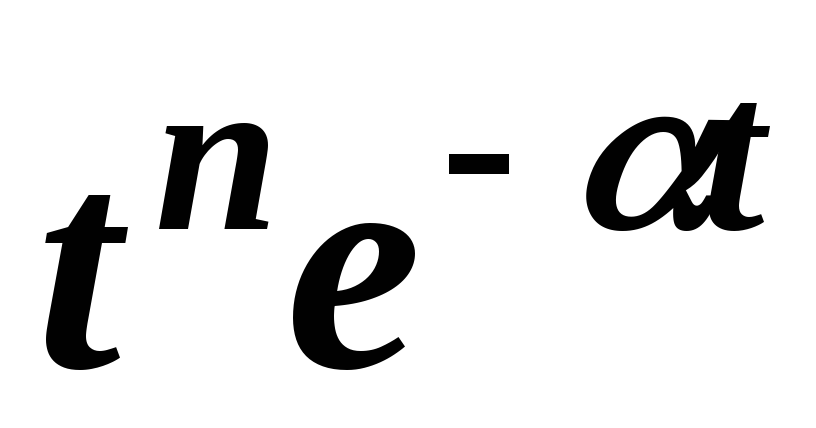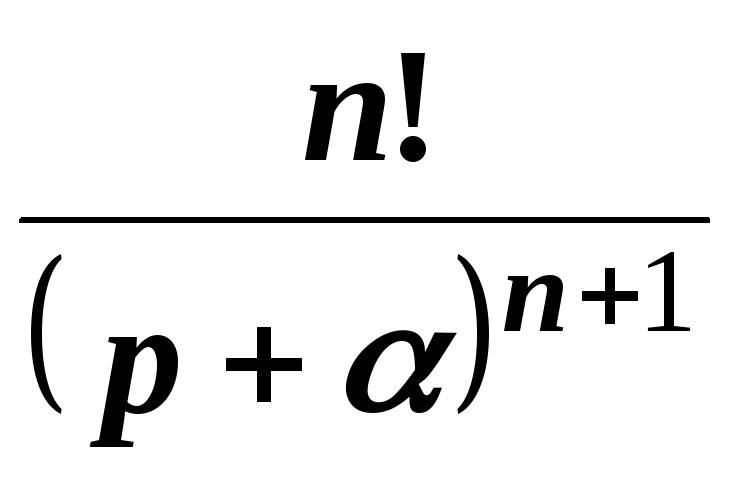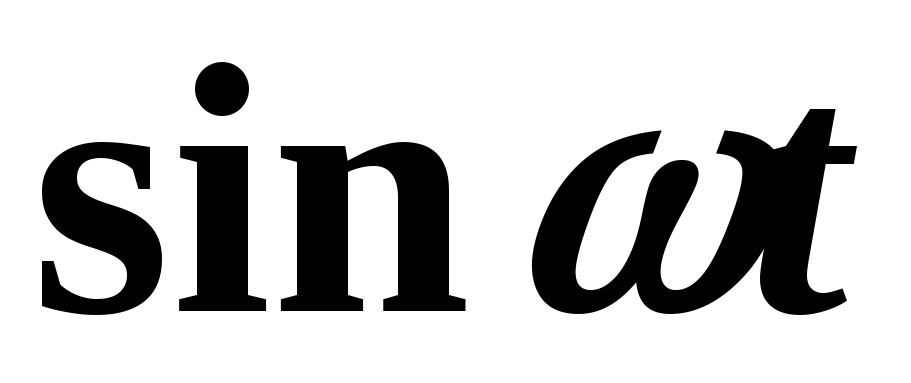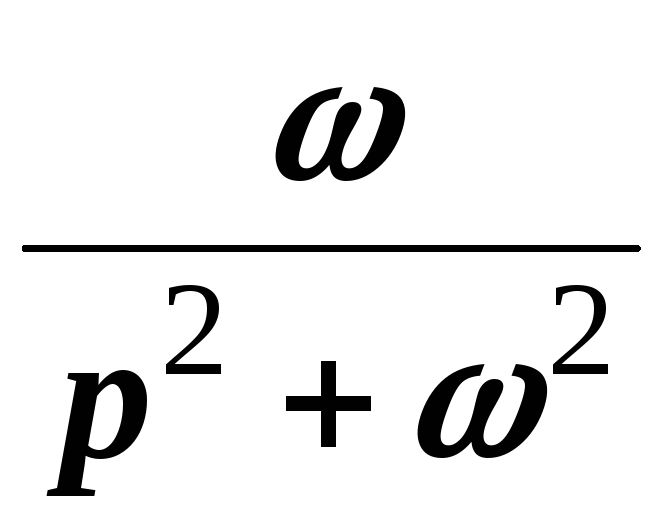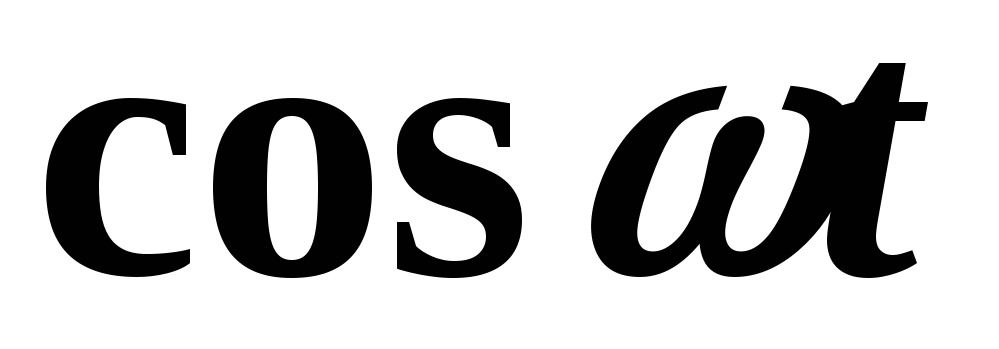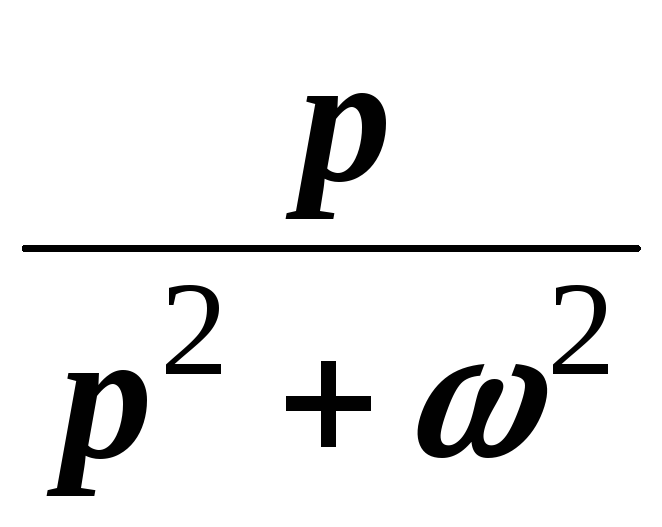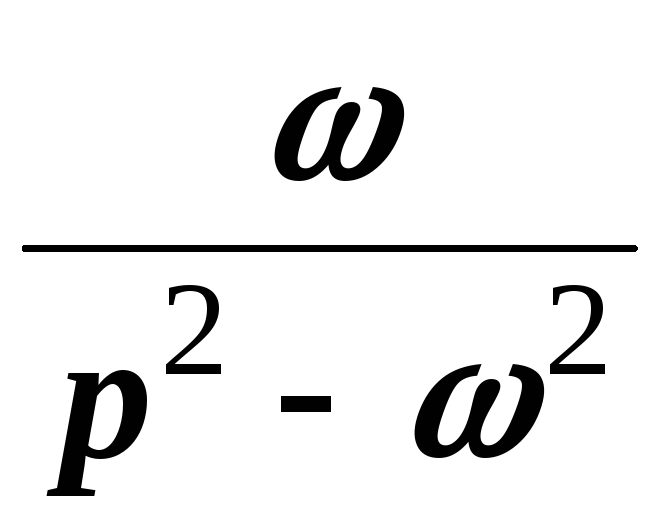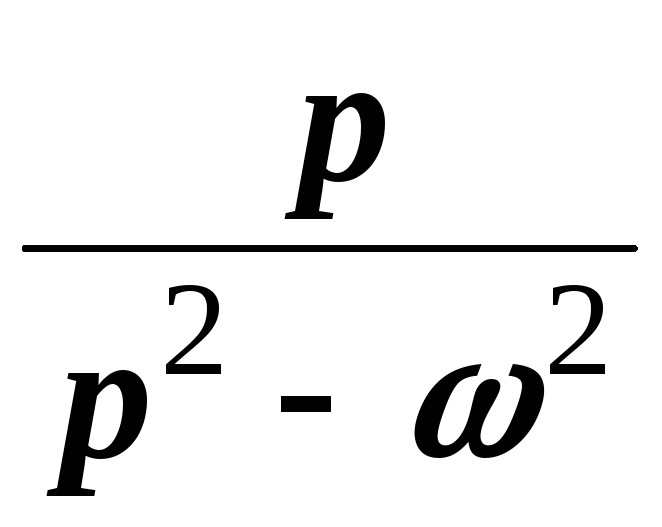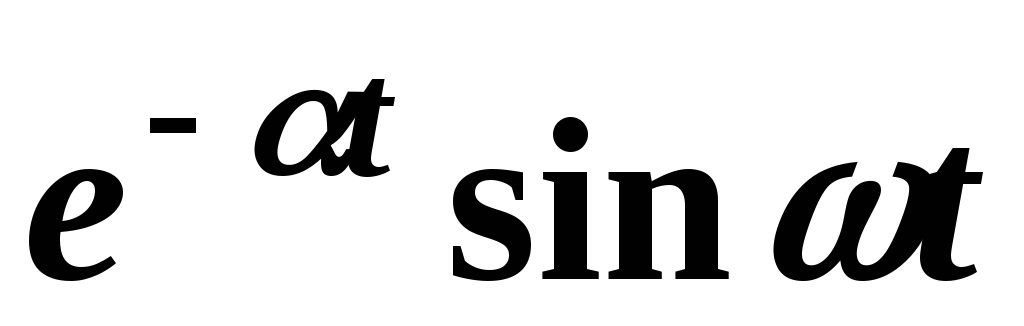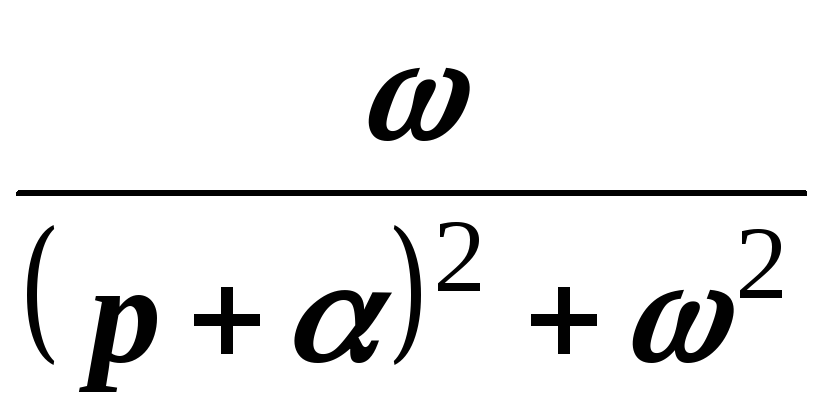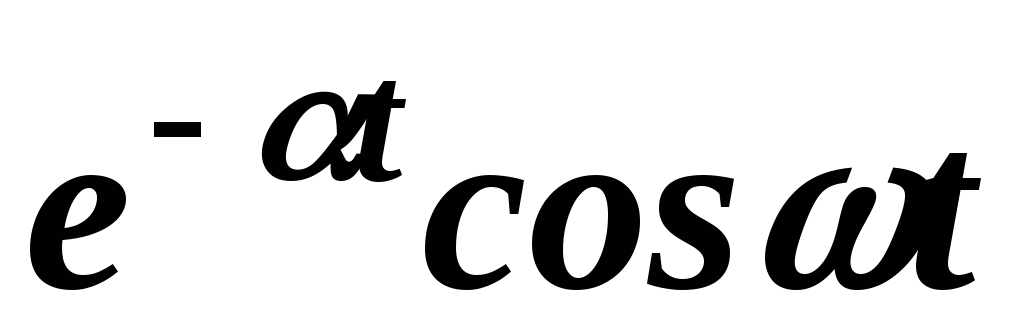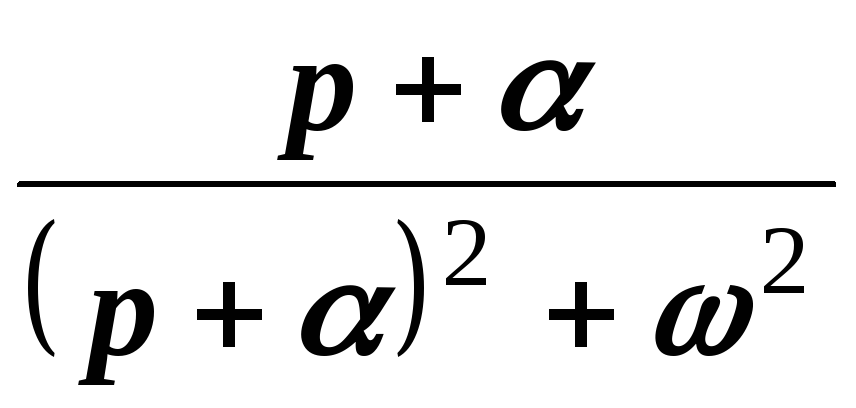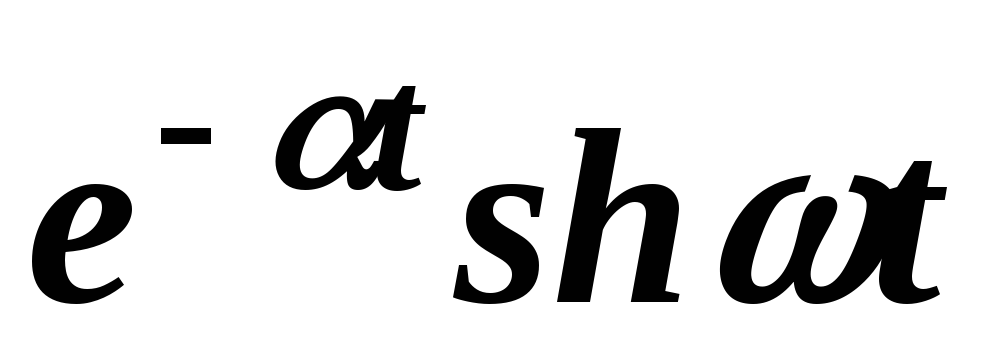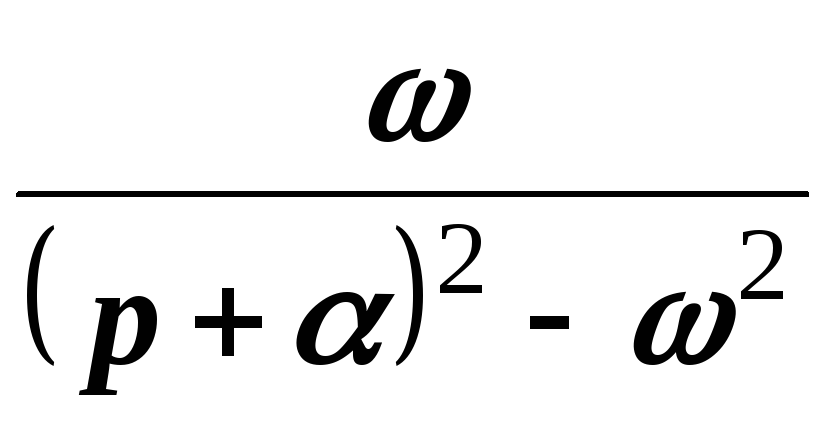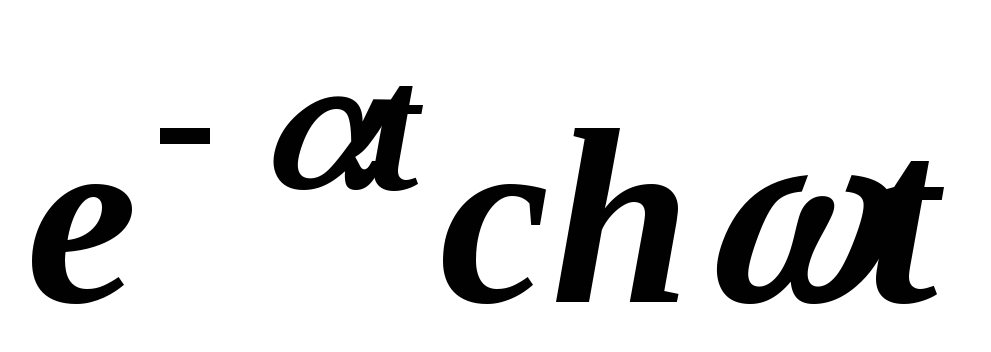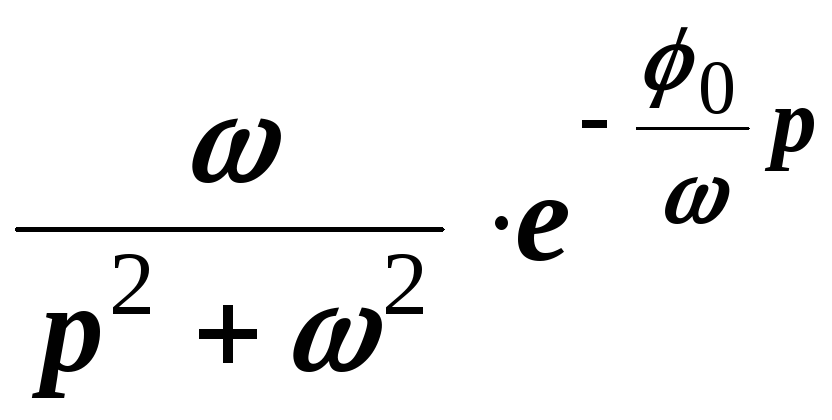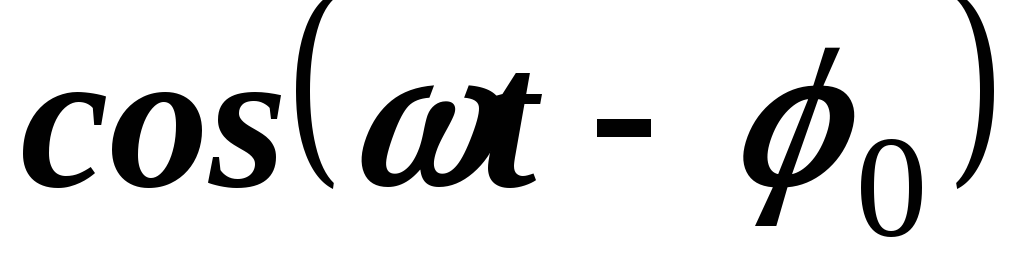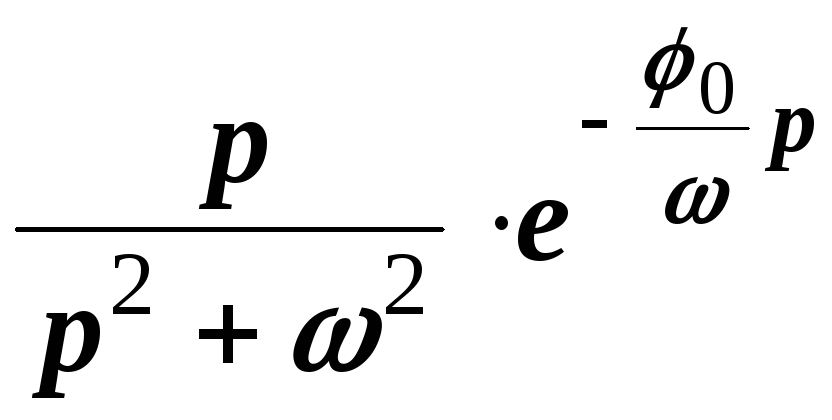| Название функции | Формула функции | График функции | Название графика | Комментарий |
|---|---|---|---|---|
| Линейная, прямая пропорциональность | y = kx | Прямая | Cамый простой частный случай линейной зависимости — прямая пропорциональность у = kx, где k ≠ 0 — коэффициент пропорциональности. На рисунке пример для k = 1, т.е. фактически приведенный график иллюстрирует функциональную зависимость, которая задаёт равенство значения функции значению аргумента. | |
| Линейная, прямая пропорциональность со сдвигом | y = kx + b | Прямая | Общий случай линейной зависимости: коэффициенты k и b — любые действительные числа. Здесь k = 0.5, b = -1. | |
| Квадратичная функция | y = x2 | Парабола | Простейший случай квадратичной зависимости — симметричная парабола с вершиной в начале координат. | |
| Квадратичная функция | y = ax2 + bx + c | Парабола | Общий случай квадратичной зависимости: коэффициент a — произвольное действительное число не равное нулю (a принадлежит R, a ≠ 0), b, c — любые действительные числа | |
| Степенная функция | y = x3 | Кубическая парабола | Самый простой случай для целой нечетной степени. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций». | |
| Степенная — корень квадратный | y = x1/2 | График функции y = √x |
Самый простой случай для дробной степени (x1/2 = √x). Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций». | |
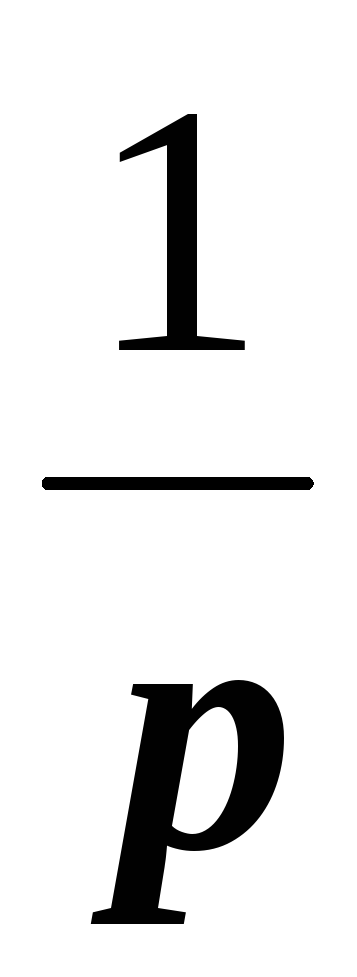
| Степенная — обратная пропорциональность | y = k/x | Гипербола | Самый простой случай для целой отрицательной степени (1/x = x-1) — обратно-пропорциональная зависимость. Здесь k = 1. | |
| Показательная функция | y = ex | Экспонента | Экспоненциальной зависимостью называют показательную функцию для основания e — иррационального числа примерно равного 2,7182818284590… | |
| Показательная функция | y = ax | График показательной функции а>1 | ||
| Показательная функция | y = ax | График показательной функции 0<a<1 | Показательная функция определена для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = 0,5x (a = 1/2 < 1). | |
| Логарифмическая функция | y = ln(x) | График логарифмической функции — натуральный логарифм | График логарифмической функции для основания e (натурального логарифма) иногда называют логарифмикой. | |
| Логарифмическая функция | y = log ax | График логарифмической функции — логарифм по основанию а>1 | Логарифмы определены для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = log2x (a = 2 > 1). | |
| Логарифмическая функция | y = logax | График логарифмической функции 0<a<1 | Логарифмы определены для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = log0,5x (a = 1/2 < 1). | |
| Синус | y = sinx | Синусоида | Тригонометрическая функция синус. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций». | |
| Косинус | y = cosx | Косинусоида | Тригонометрическая функция косинус. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций». | |
| Тангенс | y = tgx | Тангенсоида | Тригонометрическая функция тангенс. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций». | |
| Котангенс | y = сtgx | Котангенсоида | Тригонометрическая функция котангенс. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций». |
Алгебра. Урок 5. Графики функций
Смотрите бесплатные видео-уроки на канале Ёжику Понятно по теме “Графики функций”.

Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Система координат – это две взаимно перпендикулярные координатные прямые, пересекающиеся в точке, которая является началом отсчета для каждой из них.
Координатные оси – прямые, образующие систему координат.
Ось абсцисс (ось x ) – горизонтальная ось.
Ось ординат (ось y ) – вертикальная ось.

Функция – это отображение элементов множества X на множество Y. При этом каждому элементу x множества X соответствует одно единственное значение y множества Y.
Линейная функция – функция вида y=ax+b где a и b – любые числа.
Графиком линейной функции является прямая линия.
Рассмотрим, как будет выглядеть график в зависимости от коэффициентов a и b:
Если a>0, прямая будет проходить через I и III координатные четверти.
b – точка пересечения прямой с осью y.

Если a<0, прямая будет проходить через II и IV координатные четверти.
b – точка пересечения прямой с осью y.

Если a=0, функция принимает вид y=b.

Отдельно выделим график уравнения x=a.
Важно: это уравнение не является функцией так как нарушается определение функции (функция ставит в соответствие каждому элементу x множества X одно единственно значение y множества Y). Данное уравнение ставит в соответствие одному элементу x бесконечное множества элементов y. Тем не менее, график данного уравнения построить можно. Просто не будем называть его гордым словом «Функция».

Графиком функции y=ax2+bx+c является парабола.
Для того, чтобы однозначно определить, как располагается график параболы на плоскости, нужно знать, на что влияют коэффициенты a,b,c:
- Коэффициент a указывает на то, куда направлены ветки параболы.
- Если a>0 , ветки параболы направлены вверх.
- Если a<0 , ветки параболы направлены вниз.
- Коэффициент c указывает, в какой точке парабола пересекает ось y.
- Коэффициент b помогает найти xв – координату вершины параболы.
xв=−b2a
- Дискриминант позволяет определить, сколько точек пересечения у параболы с осью .
- Если D>0 – две точки пересечения.
- Если D=0 – одна точка пересечения.
- Если D<0 – нет точек пересечения.
Графиком функции y=kx является гипербола.
Характерная особенность гиперболы в том, что у неё есть асимптоты.
Асимптоты гиперболы – прямые, к которым она стремится, уходя в бесконечность.
Ось x – горизонтальная асимптота гиперболы
Ось y – вертикальная асимптота гиперболы.
На графике асимптоты отмечены зелёной пунктирной линией.
Если коэффициент k>0, то ветви гиперолы проходят через I и III четверти.

Если k < 0, ветви гиперболы проходят через II и IV четверти.

Чем меньше абсолютная величина коэффиента k (коэффициент k без учета знака), тем ближе ветви гиперболы к осям x и y.
Функция y = x имеет следующий график:

Функция y = f(x)возрастает на интервале, если большему значению аргумента (большему значению x) соответствует большее значение функции (большее значение y).
То есть чем больше (правее) икс, тем больше (выше) игрек. График поднимается вверх (смотрим слева направо)
Примеры возрастающих функций:

Функция y = f(x)убывает на интервале, если большему значению аргумента (большему значению x) соответствует меньшее значение функции (большее значение y).
То есть чем больше (правее) икс, тем меньше (ниже) игрек. График опускается вниз (смотрим слева направо).
Примеры убывающих функций:

Для того, чтобы найти наибольшее значение функции, находим самую высокую точку на графике и смотрим, какая у нее координата по оси ординат (по оси y). Это значение и будет являться наибольшим значением функции.

Для того, чтобы найти наименьшее значение функции, находим самую нижнюю точку на графике и смотрим, какая у нее координата по оси ординат (по оси y). Это значение и будет являться наименьшим значением функции.

Скачать домашнее задание к уроку 5.
2. Нахождение изображения функций. Примеры
Пример 1. Найти изображение единичной функции Хевисайда, которая обозначается и определяется в соответствии с равенством:
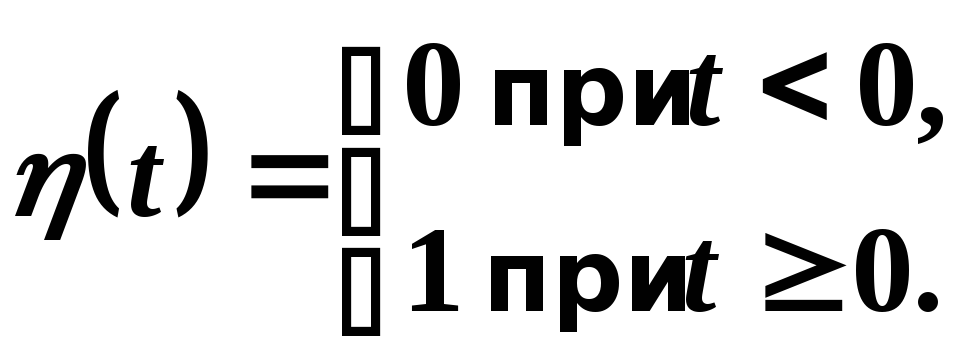
Решение. Пользуясь определением изображения по Лапласу, находим
.
Пример 2. Найти изображение функции
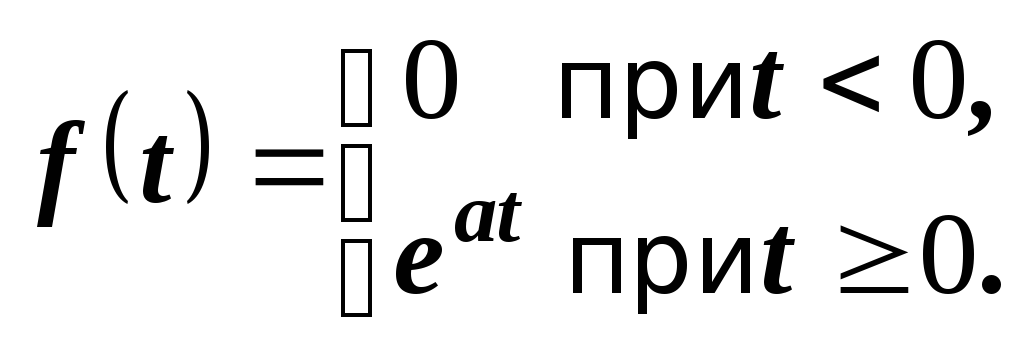
Решение. Имеем
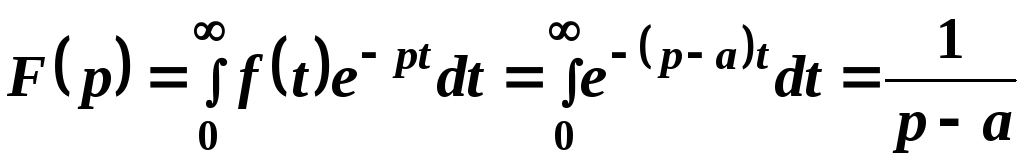 .
.
Заметим, что указанную функцию можно записать короче, если использовать в качестве множителя единичную функцию (t), а именно:
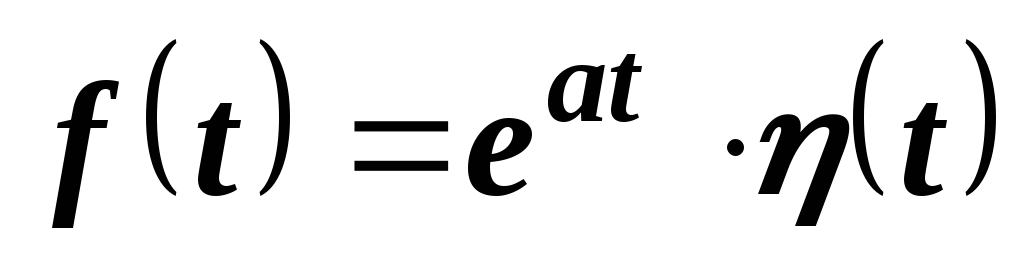 .
.
Роль множителя (t) состоит в том, что он «гасит» (обращает в нуль) функцию при t < 0. В дальнейшем, говоря о функциях-оригиналах, будем считать, что все они снабжены множителем (t), хотя сам этот множитель в написании часто будем опускать. Так, например, мы будем писать tn, eat, sint и т. д., подразумевая при этом соответственно

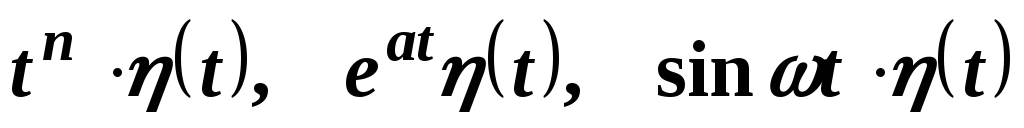 и т. д.
и т. д.
Единичная
функция играет важную роль в операционном
исчислении. Зная ее изображение и
используя правила операционного
исчисления, можно найти изображения
различных оригиналов. Например, используя
теорему смещения, можно записать: из
того, что 
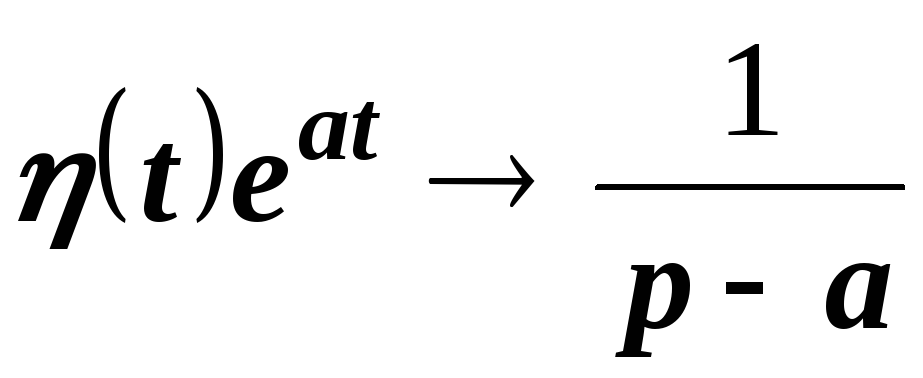 ,
,и не пользоваться определением преобразования Лапласа, связанного с вычислением несобственного интеграла.
Пример 3. Найти изображения функций 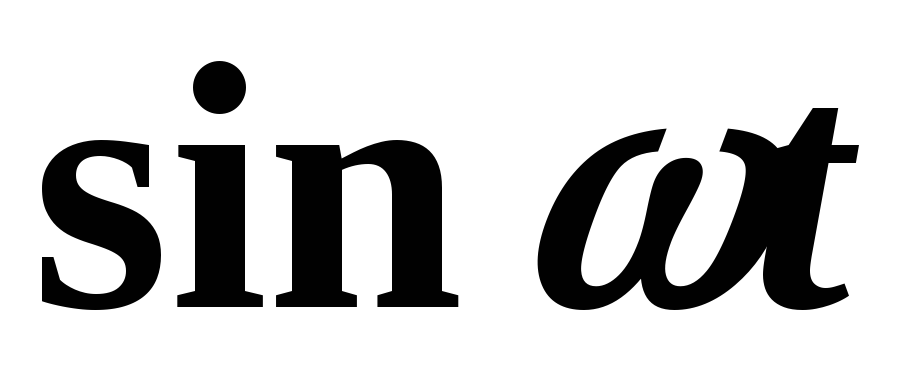 и
и 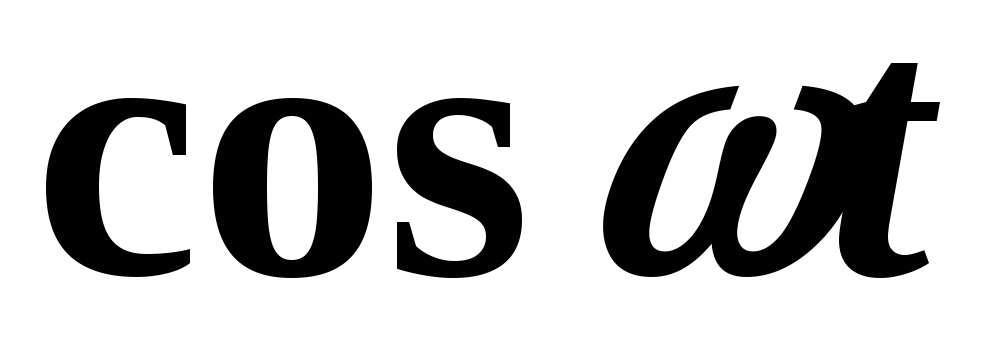 .
.
Решение. Воспользуемся формулами Эйлера:
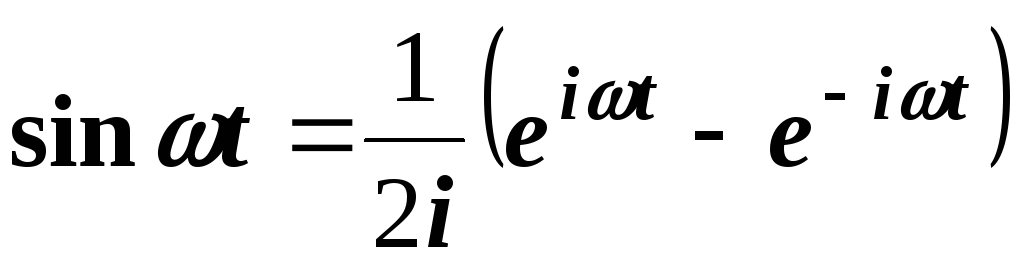 ;
;
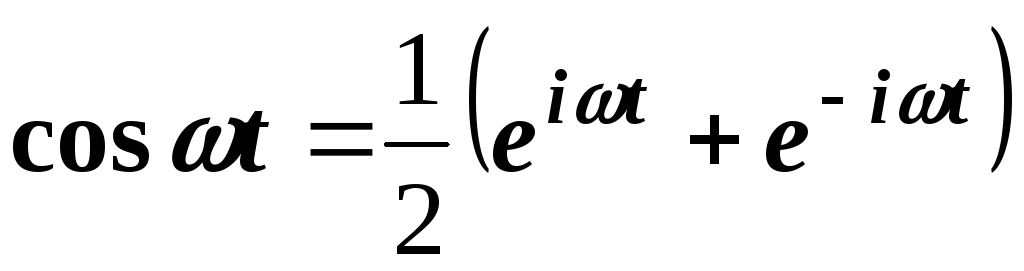 .
.
Согласно свойству линейности преобразования Лапласа имеем
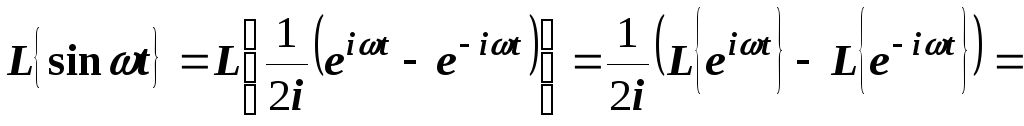
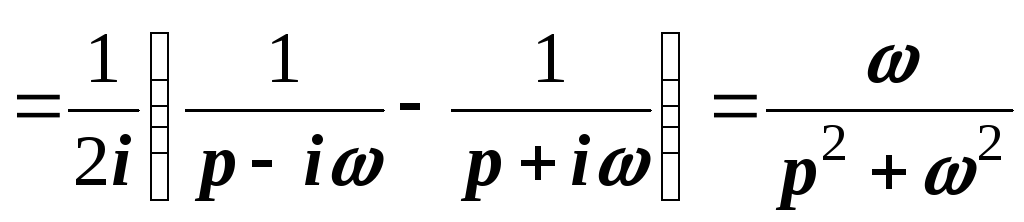 .
.
Следовательно,
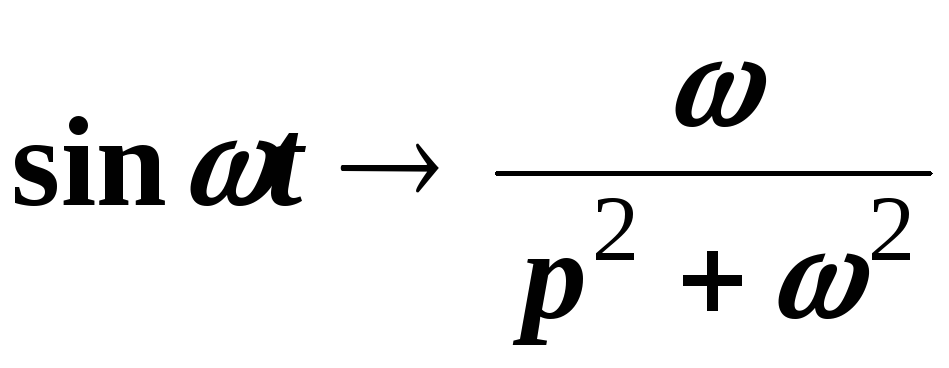 .
.
Точно также
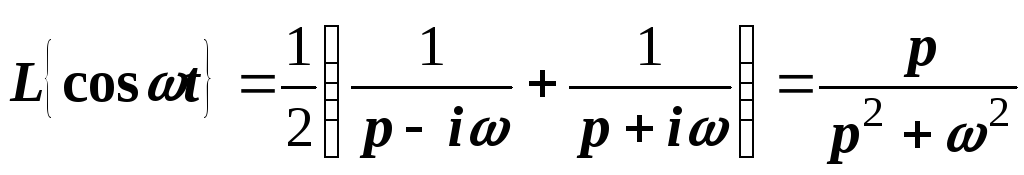 ,
,
то есть
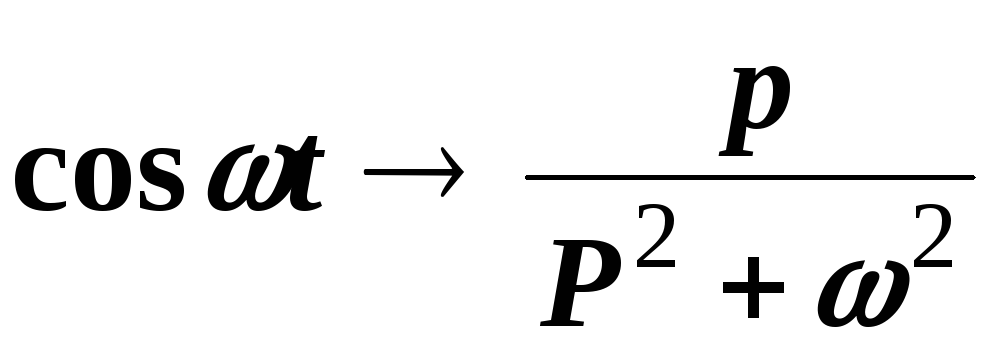 .
.
Применяя к полученным соотношениям свойство смещения, находим
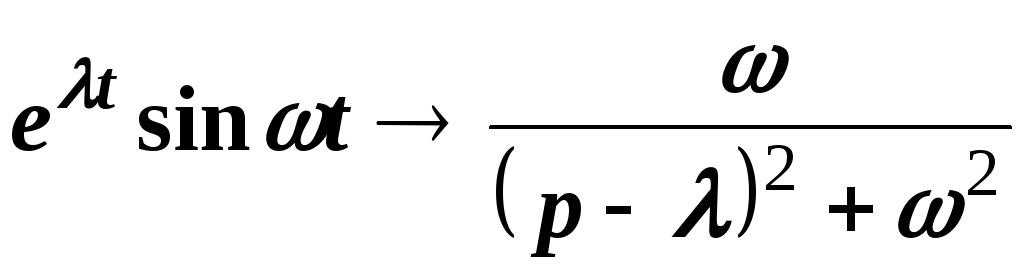 ,
,
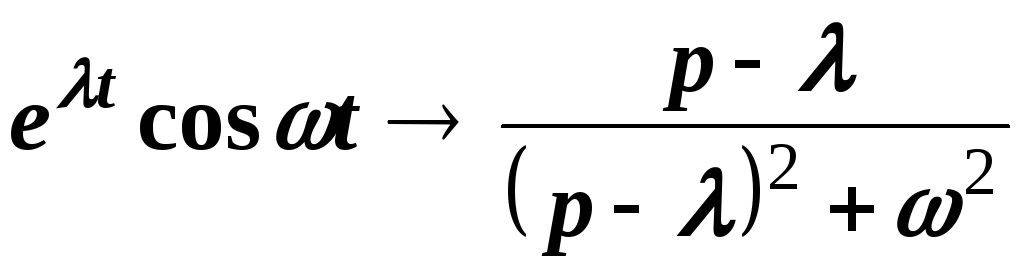
Точно также для гиперболических функций получаем соответствия:
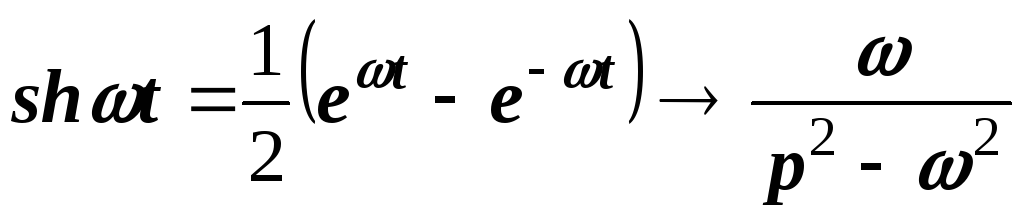 ;
;
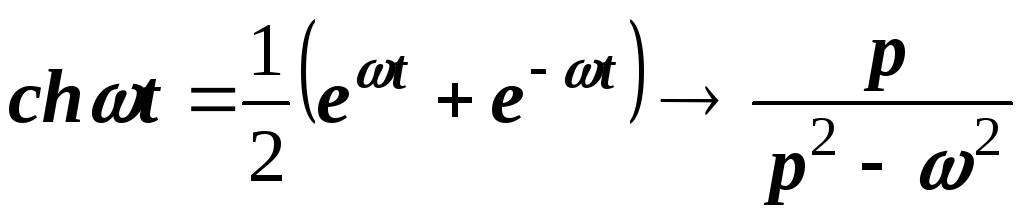 .
.
Пример 4. Найти изображение функции tn.
Решение. Используем теорему дифференцирования к изображению функции (t) . Получим
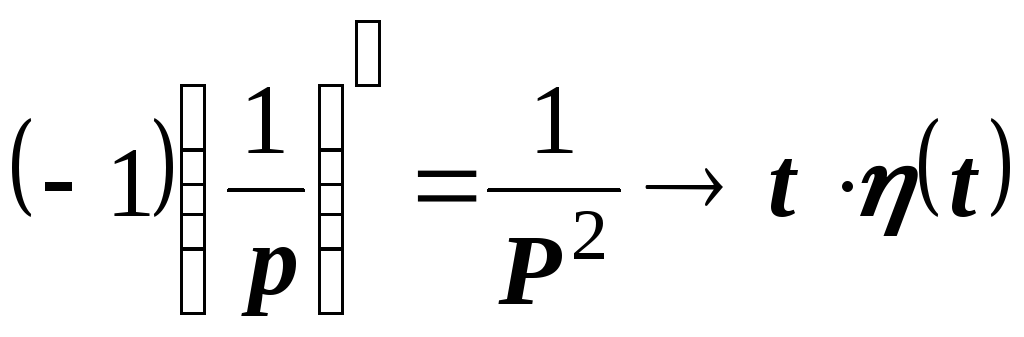 ;
; 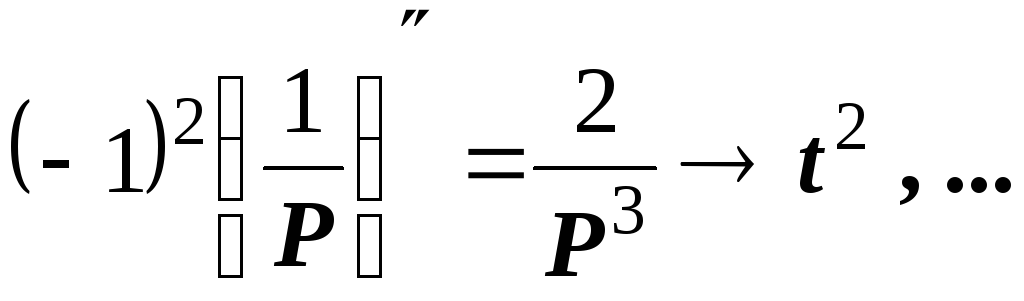 .
.
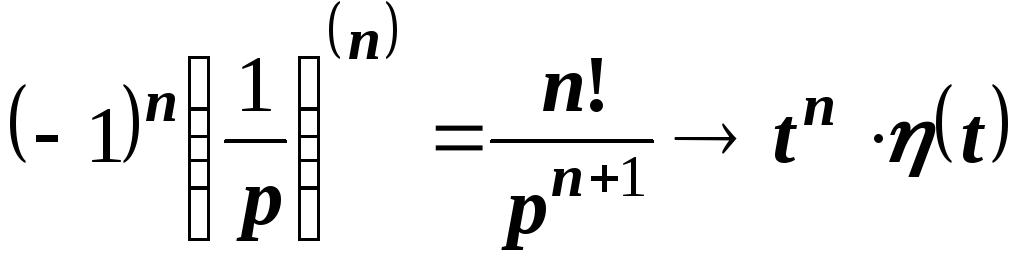 .
.
Итак, 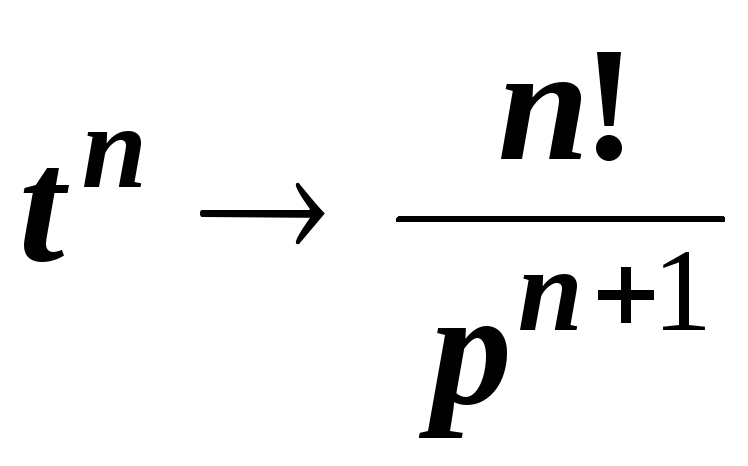
Пример 5. Найти изображение функции
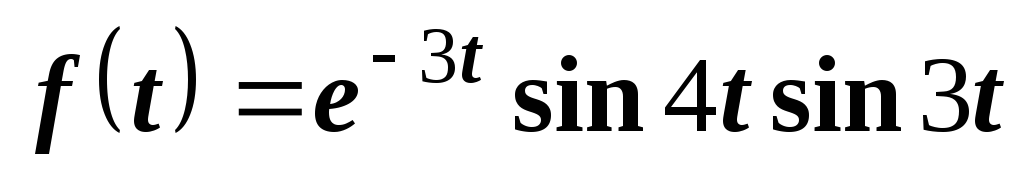 .
.
Решение. На основании формулы
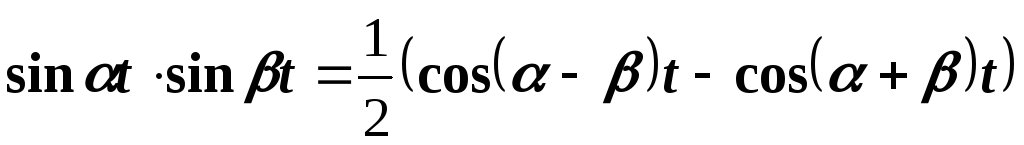
заменим
произведение 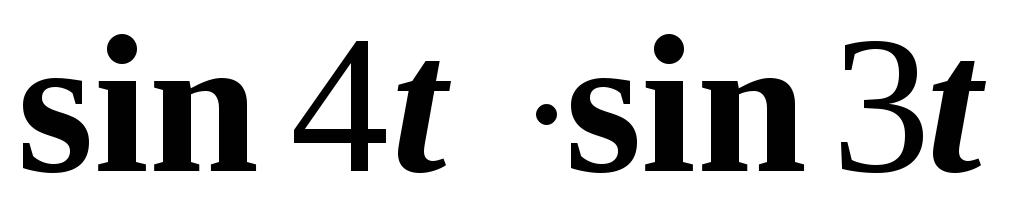 на
на 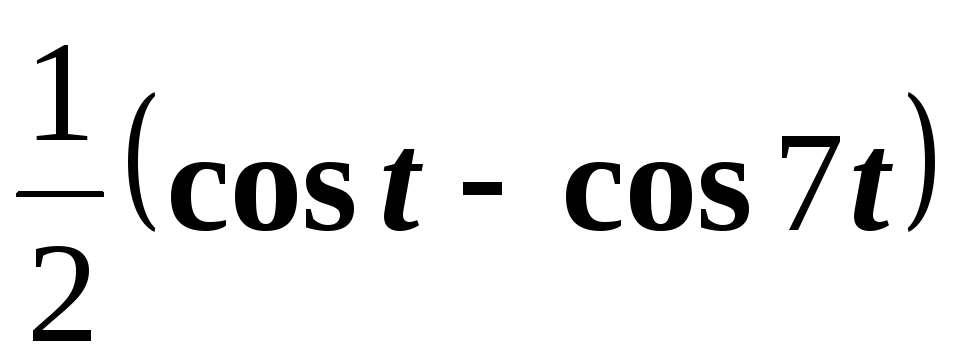 .
.
Тогда
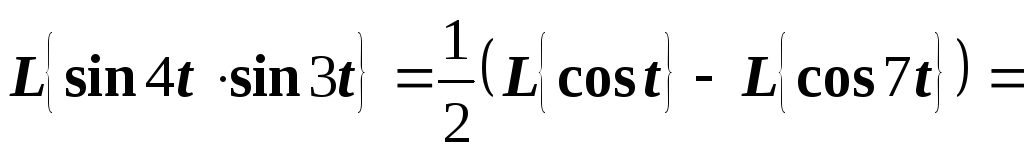
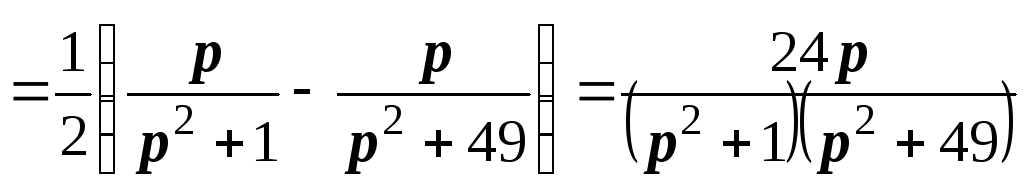 .
.
Чтобы
найти изображение исходной функции,
воспользуемся тем, что операции умножения
на 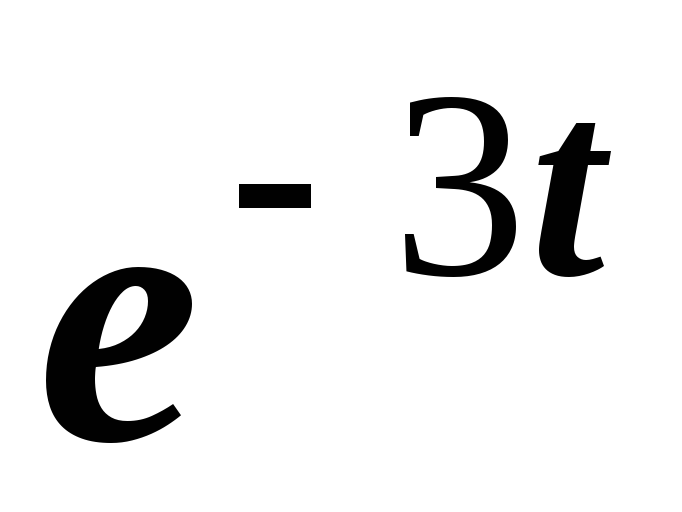 в области оригиналов соответствует
операция смещения на 3 в области
изображений. Окончательно получим
в области оригиналов соответствует
операция смещения на 3 в области
изображений. Окончательно получим
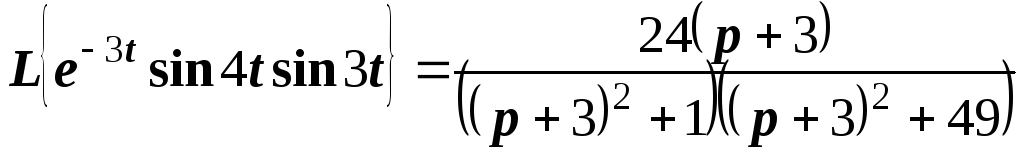 .
.
Пример 6. Найти изображение функции
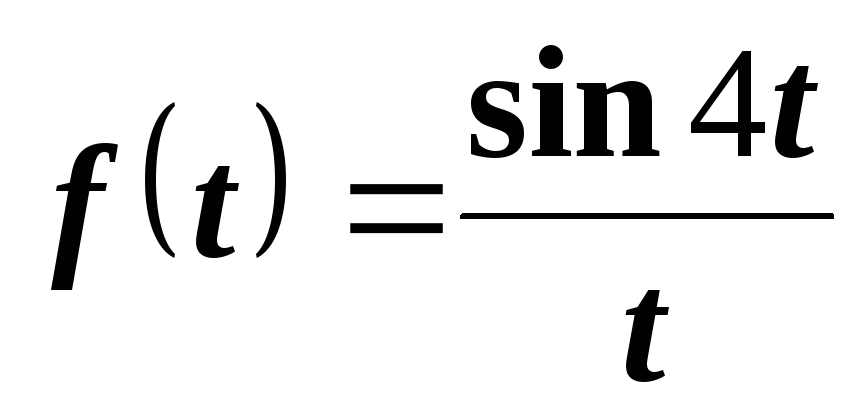 .
.
Решение. Воспользуемся соотношением
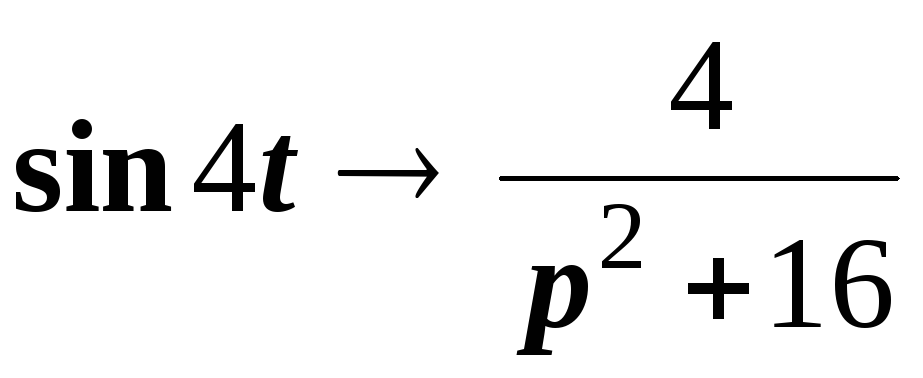 .
.
Далее, согласно правилу (8), операции деления на t в области оригиналов соответствует операция интегрирования в области изображений.
Поэтому
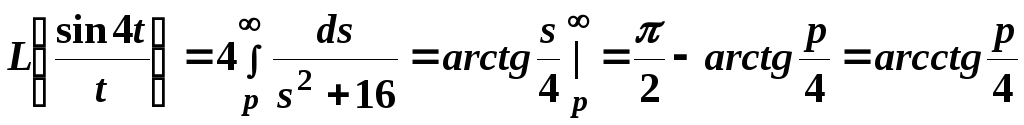 .
.
Итак,
 .
.
Пример 7. Найти изображение функции
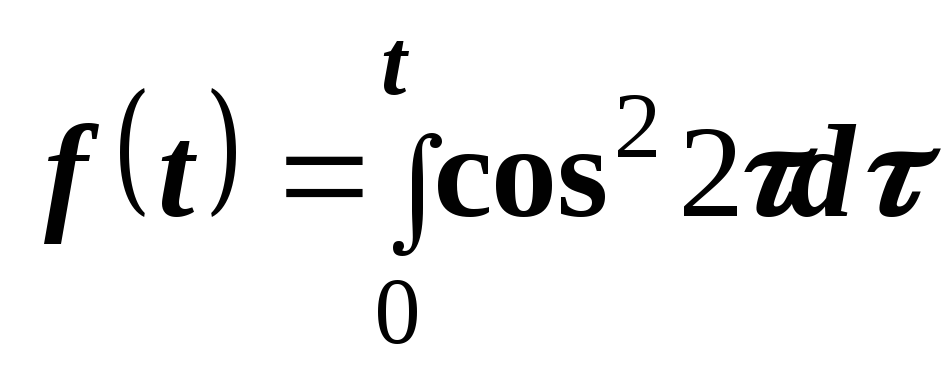 .
.
Решение.
Предварительно найдем изображение
функции 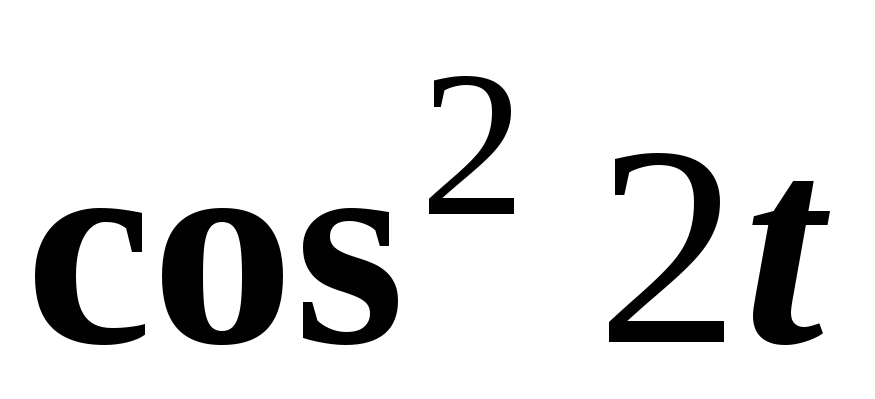 ,
преобразовав ее по формуле
,
преобразовав ее по формуле 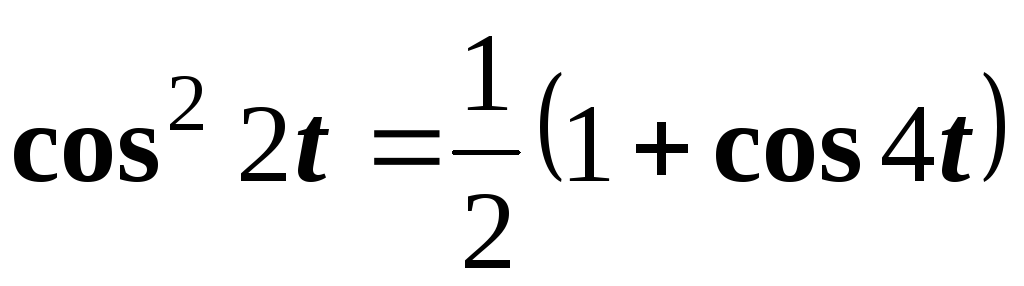 .
Имеем
.
Имеем
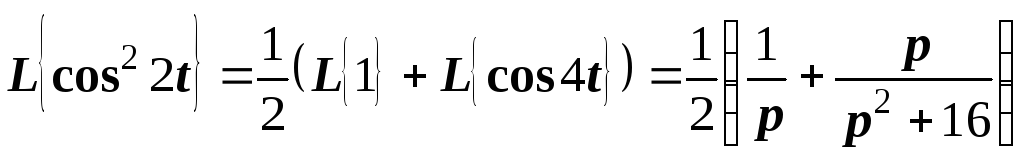 .
.
Затем, используя тот факт, что операции интегрирования в области оригиналов соответствует операция деления на р в области изображений, окончательно получим
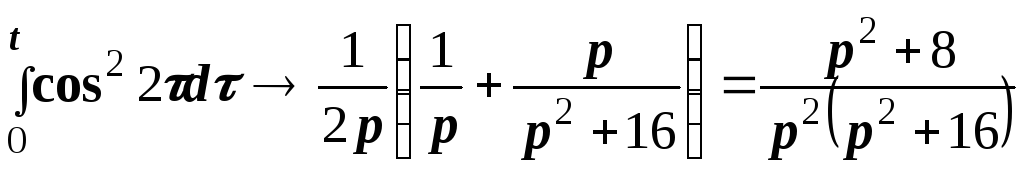 .
.
Пример 8. Найти изображение функции
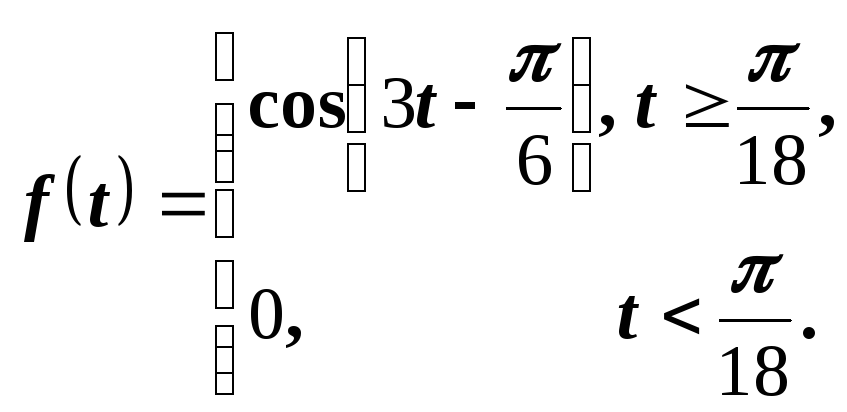
Решение.
Воспользуемся равенством 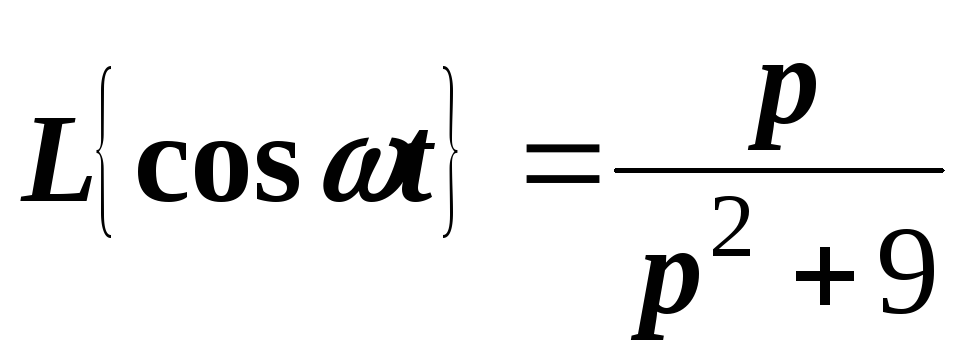 .
Согласно теореме запаздывания имеем
.
Согласно теореме запаздывания имеем
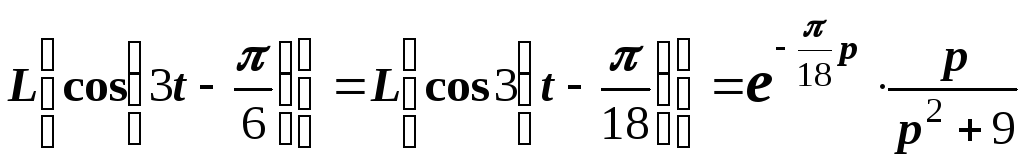 .
.
В
данном примере существенно равенство
нулю функции при 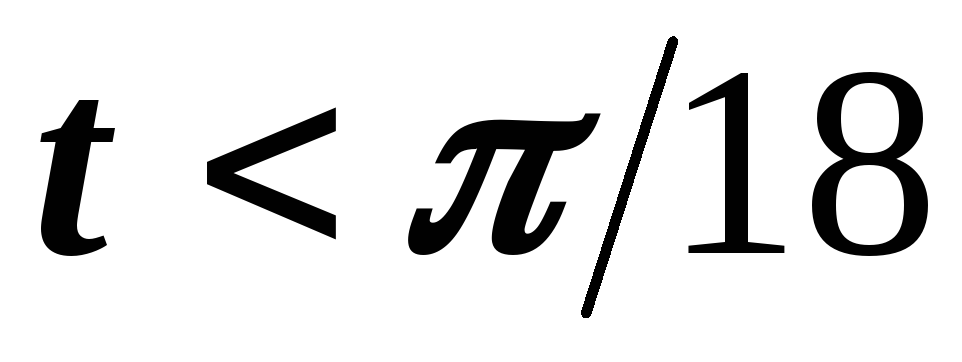 ,
т.е. возможность представления функции f(t) в виде
,
т.е. возможность представления функции f(t) в виде
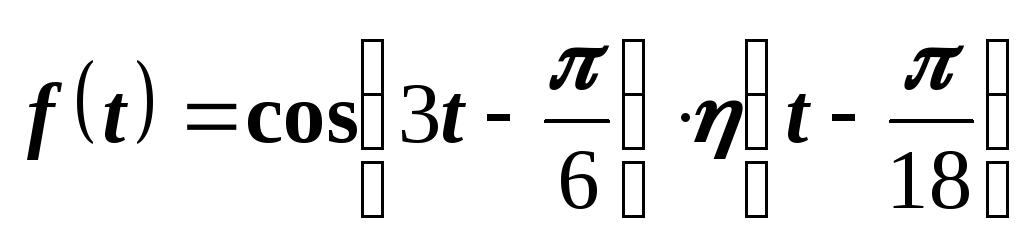 ,
,
а соответственно, и возможность использования теоремы запаздывания.
Иначе поступаем, если функция задана следующим соотношением:
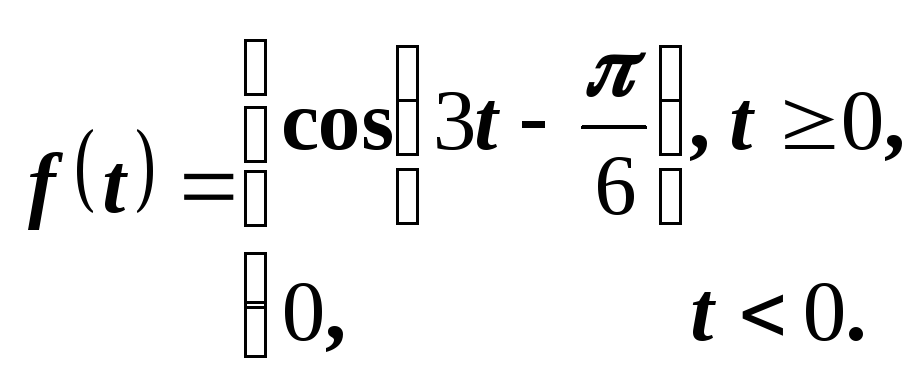
В
этом случае осуществлен сдвиг вправо
на 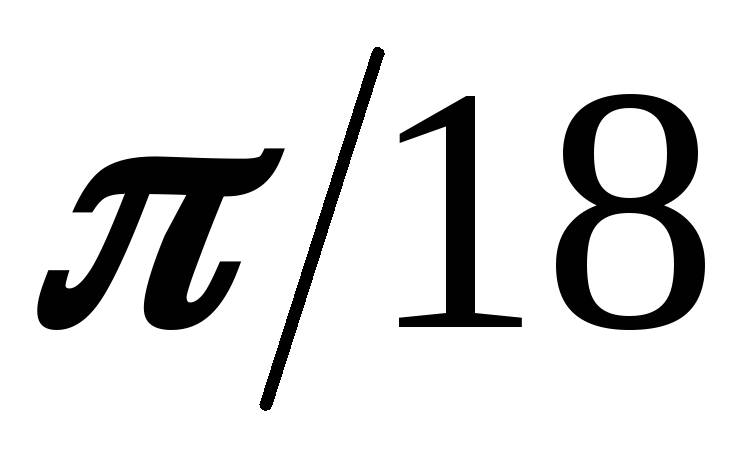 графика функции
графика функции  ,
но не произведено «погашение» его нулем
на участке
,
но не произведено «погашение» его нулем
на участке 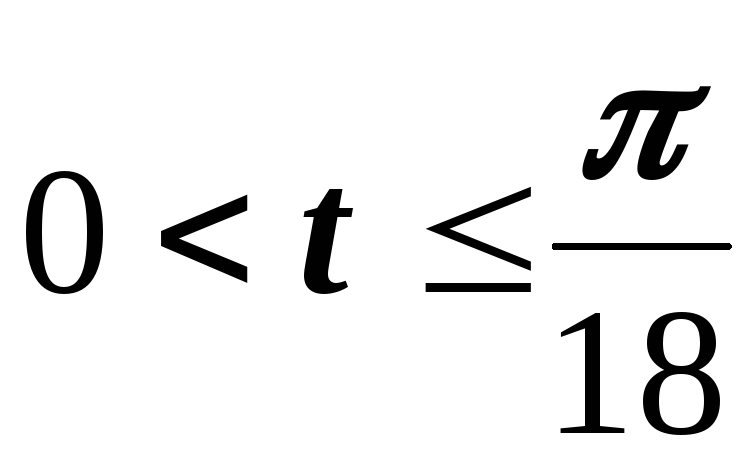 .
Поэтому запаздывания оригинала по
времени не происходит, а функция
представима в виде
.
Поэтому запаздывания оригинала по
времени не происходит, а функция
представима в виде 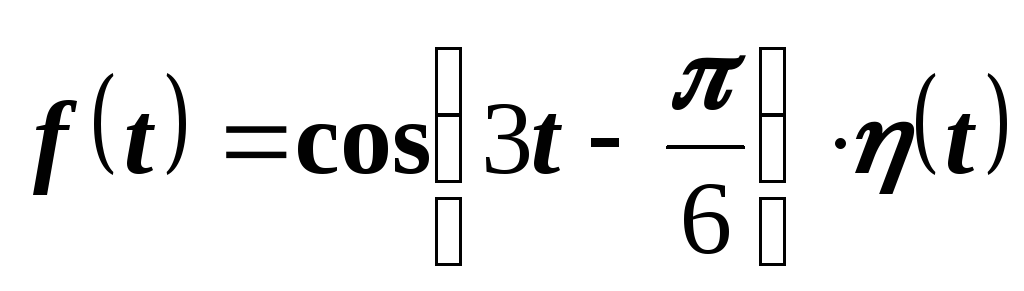 .
.
Для нахождения ее изображения воспользуемся равенством
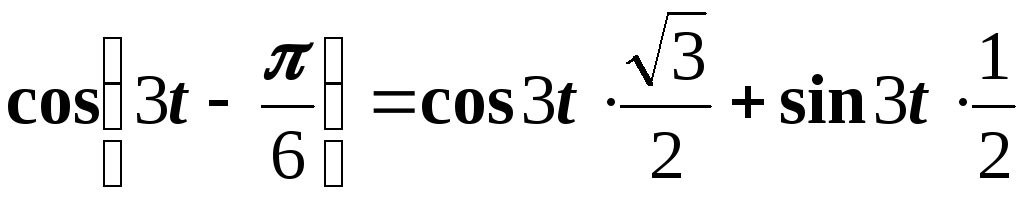 .
.
Применив теоремы подобия и линейности, получим
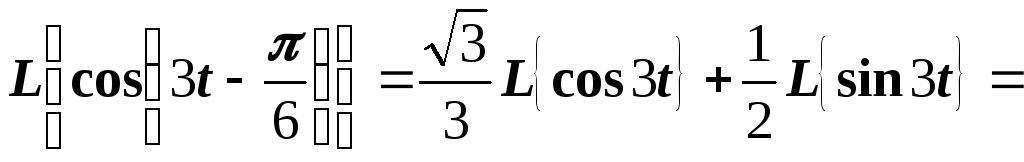
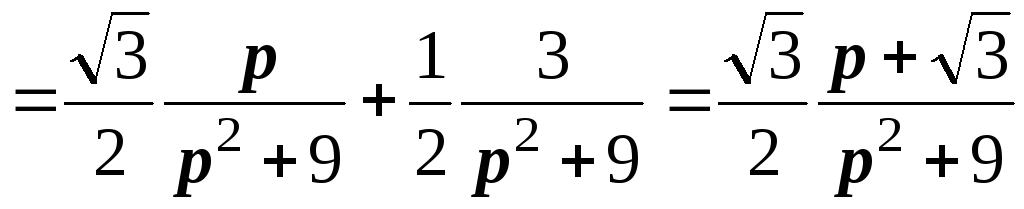 .
.
Из
этого примера следует, что при записи
оригиналов, являющихся функциями
запаздывающего аргумента 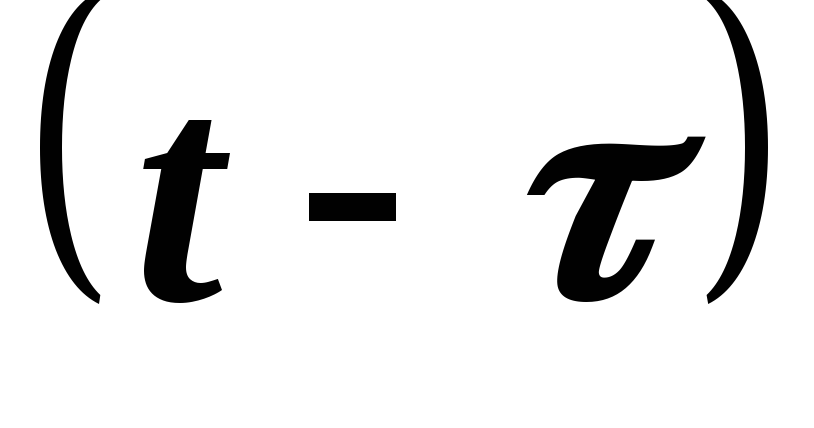 ,
опускать множитель
,
опускать множитель 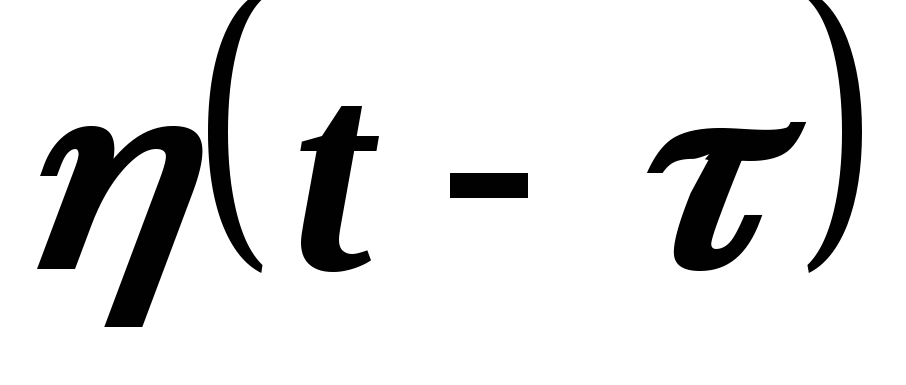 не рекомендуется во избежание
недоразумений. Так, например, для
обозначения оригиналов степенной
не рекомендуется во избежание
недоразумений. Так, например, для
обозначения оригиналов степенной 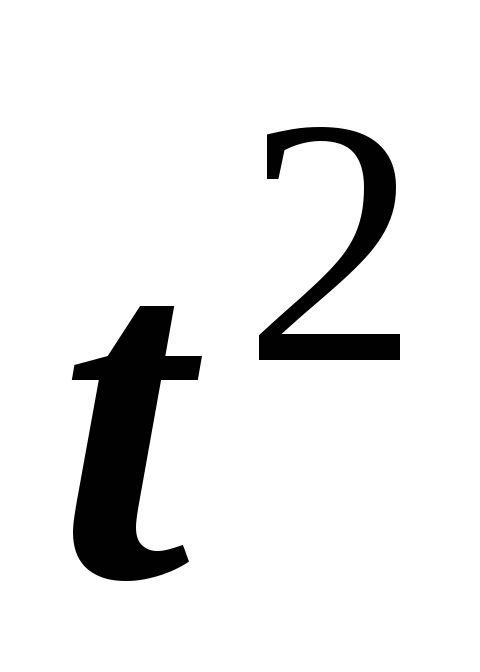 и
показательной
и
показательной 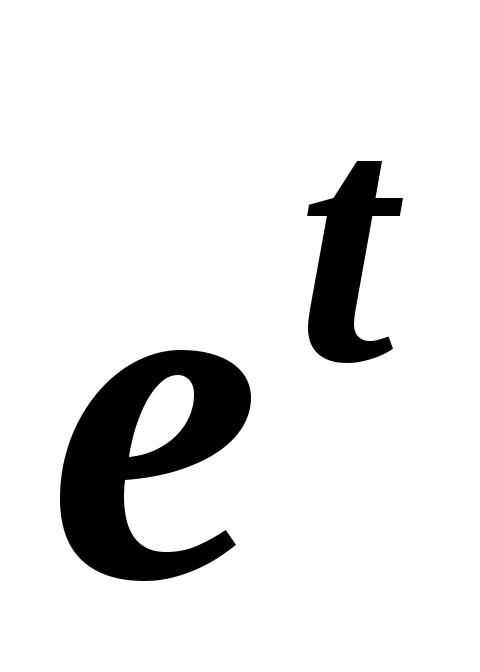 функций запаздывающего аргумента с
запаздыванием следует пользоваться записью
функций запаздывающего аргумента с
запаздыванием следует пользоваться записью 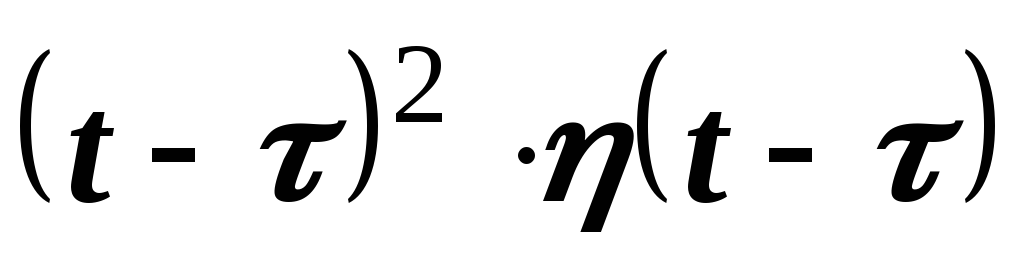 ,
, 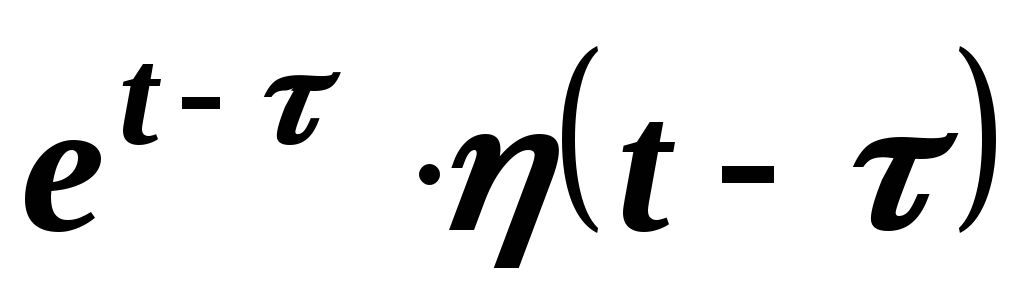 ,
а не записью
,
а не записью 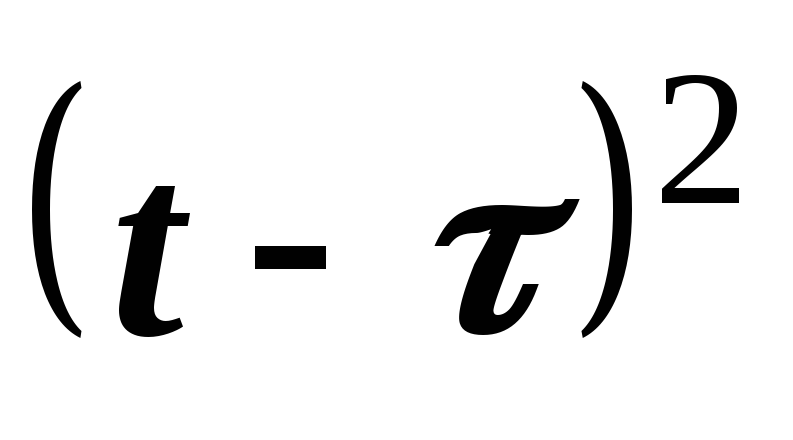 и
и 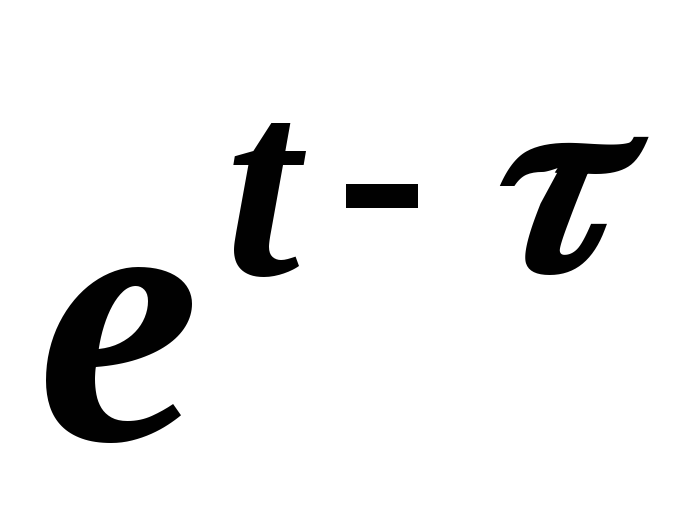 .
.
Последнюю
легко спутать с записью оригинала
незапаздывающего аргумента: 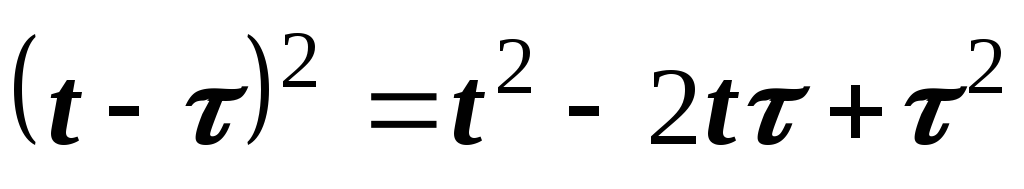 и
и 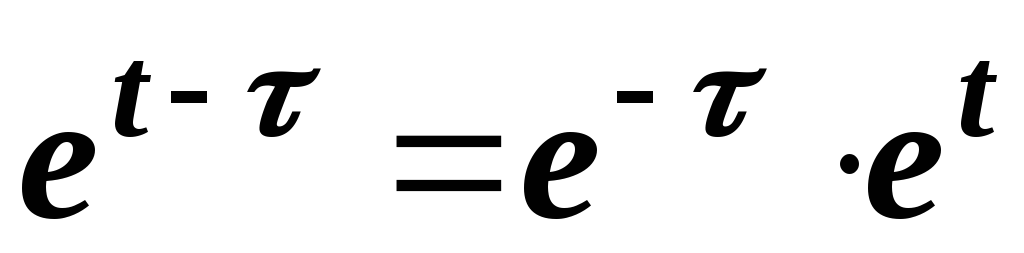 .
.
Пример 9. Найти изображение функции
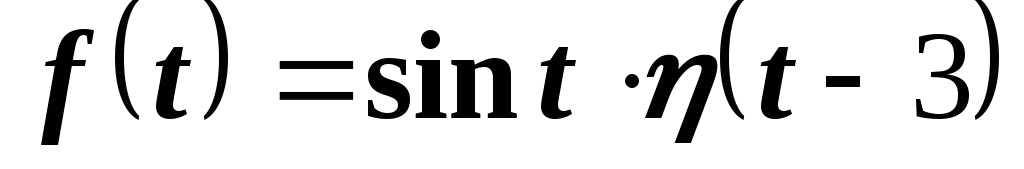 .
.
Решение.
Для того, чтобы применить теорему
запаздывания, предварительно преобразуем
оригинал как функцию аргумента 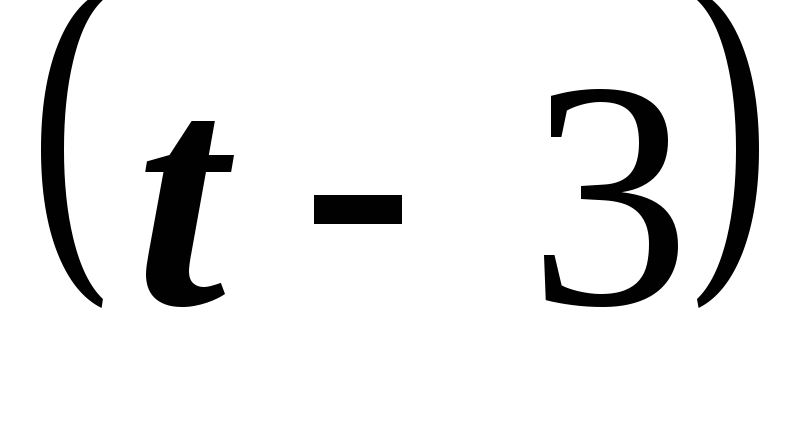 :
:
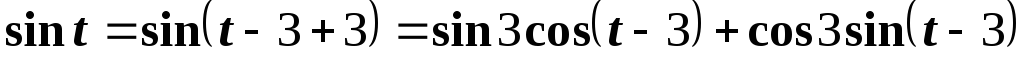 .
.
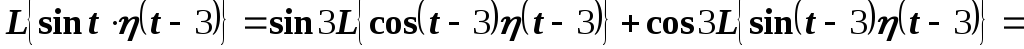
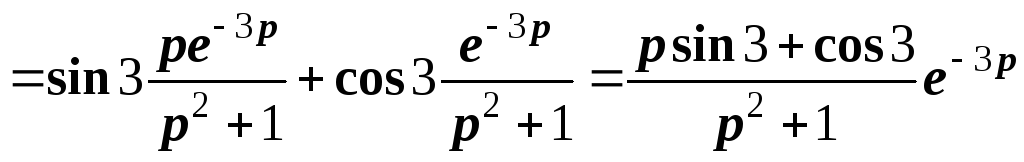 .
.
Заметим, что изображение этого оригинала можно найти согласно его определения:
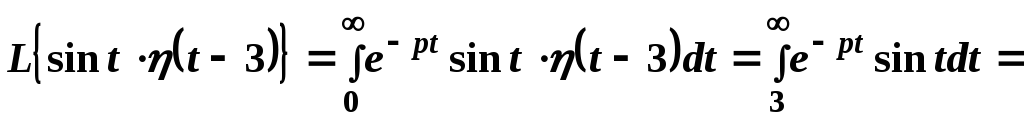
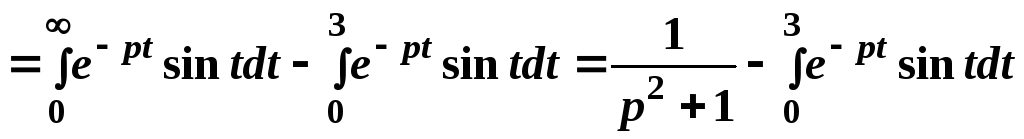 .
.
Вычислив интеграл, мы получим тот же результат.
Теорема запаздывания является удобным способом для нахождения изображений кусочно-непрерывных функций.
Пример 10. Найти изображение функции
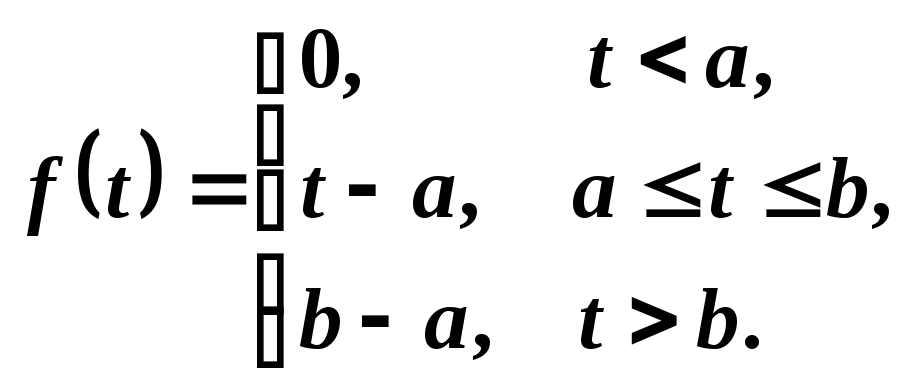
Решение. Пользуясь обобщенной единичной функцией, оригинал f(t) можно записать формулой
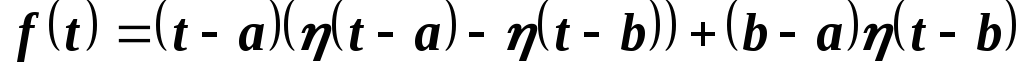 .
.
В этом равенстве отражен тот факт, что «сигнал» f1(t)=(t—a) был «включен» в момент t=a и «выключен» в момент t=b. После этого включен сигнал f2(t)=b—a.
Оригинал представим в виде
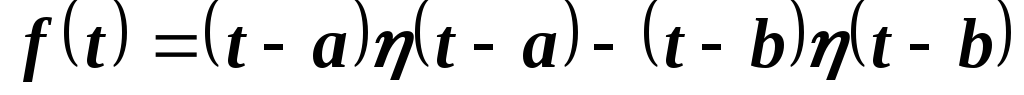 .
.
При нахождении его изображения исходим из соотношения
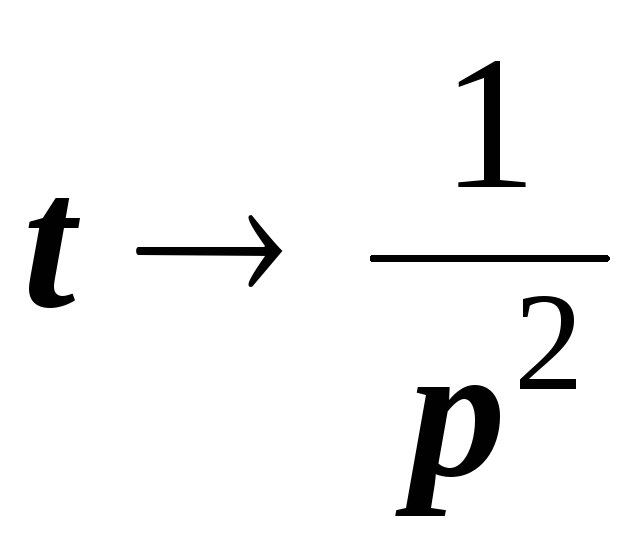 .
.
Используя теорему запаздывания оригинала, получим
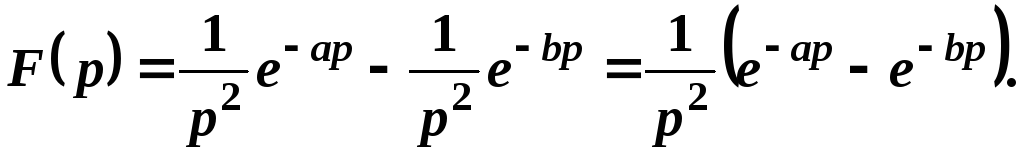
Пример 11. Найти изображение функции
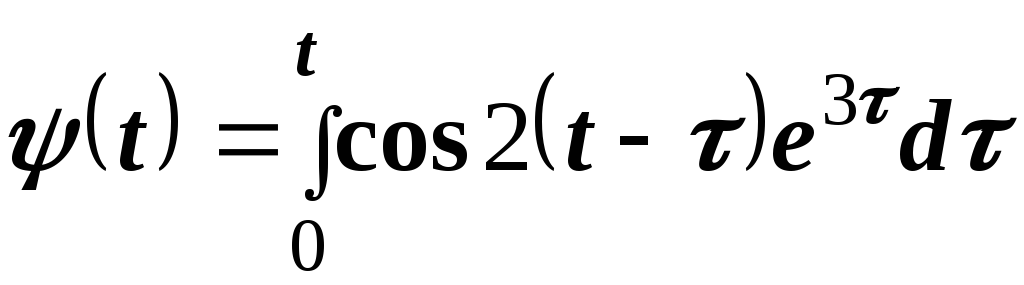 .
.
Решение.
Функция 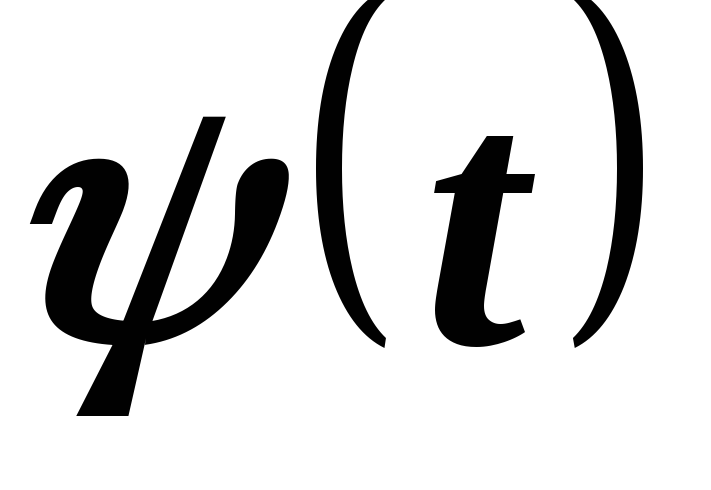 есть свертка функций
есть свертка функций 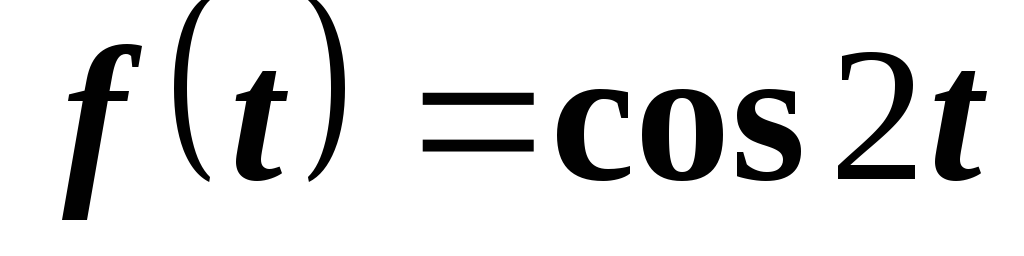 и
и 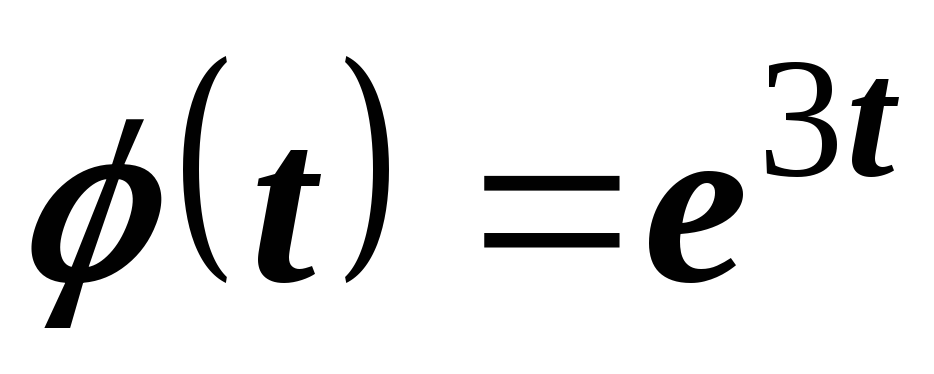 .
Согласно теореме умножения свертке
двух функций соответствует произведение
их изображений. Если учесть, что
.
Согласно теореме умножения свертке
двух функций соответствует произведение
их изображений. Если учесть, что
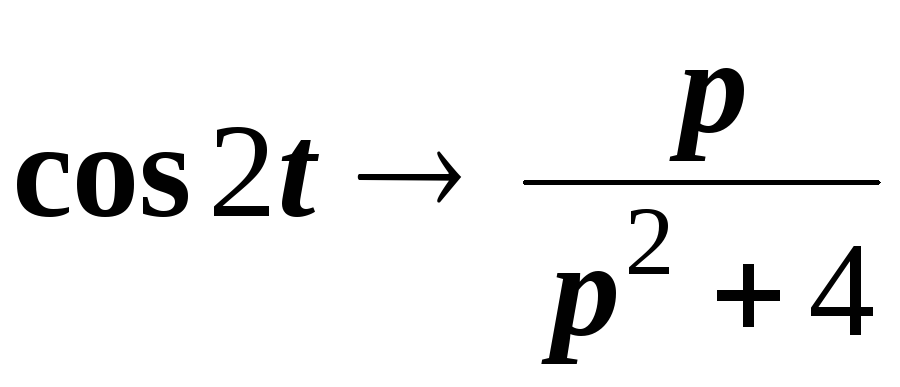 ,
а
,
а 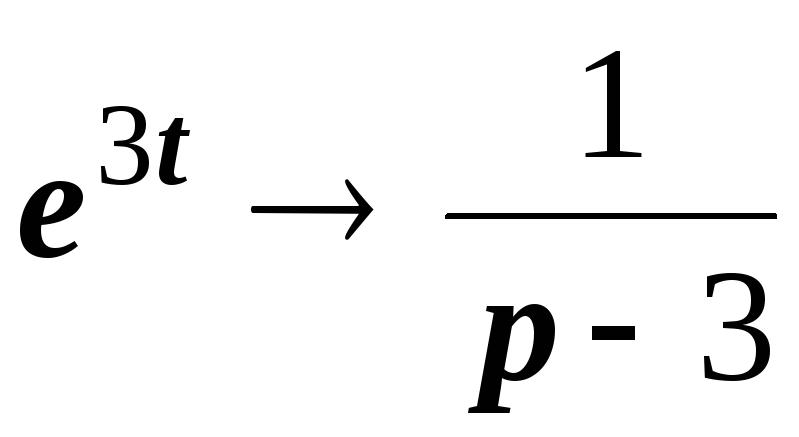 ,
,
то указанной свертке оригиналов будет соответствовать изображение
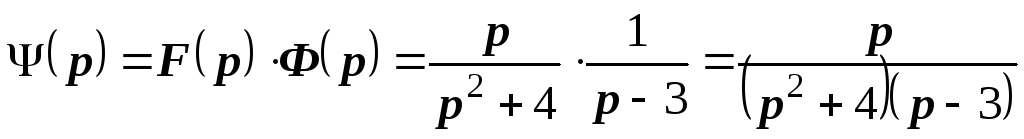 .
.
Изображения элементарных функций получаются путем вычисления соответствующих несобственных интегралов, иногда довольно сложных и громоздких. Однако нет необходимости проделывать все вычисления каждый раз заново: достаточно составить таблицу изображений и пользоваться ею подобно тому, как мы пользуемся таблицей производных или неопределенных интегралов.
Приведем таблицу изображений наиболее часто встречающихся элементарных функций (табл. 2).
Таблица 2 – Оригинал – изображение
№ | Оригинал | Изображение |
1 | 1 | |
2 | t | |
3 | tп | |
4 | | |
5 | | |
6 | | |
7 | | |
8 | | |
9 | | |
10 | | |
11 | | |
12 | | |
13 | | |
14 | | |
15 | | |
16 | | |
17 | | |
18 | | |
Квадратичная функция творит чудеса
Наступает первое сентября, и счастливые родители ведут свое чадо первый раз в первый класс. А дальше дорога для большинства учащихся длиною в 11 лет. Математика с ними на всем пути, но не у всех детей прирожденная склонность к ней.
Перед учителем встает ряд нелегких проблем. Выделим три из них:
1. Искать те крупицы воздействия на учащихся, которые способствовали бы стремлению приобретать знания, расширять их, а значит помогать начинать мыслить, включаться в урок.
2. Сделать урок таким, чтобы осталась пища для размышлений.
3. Предвидеть, что есть учащиеся с тягой к гуманитарным наукам, и стремиться помочь пробудить в них желание погрузиться в математический мир, но одновременно не забывать увлеченных математикой и давать пищу жаждущему ее уму.
Мы обратим внимание на материал статьи “Рисуем графиками функций” [3]. Автор, А. Я. Цукарь из Новосибирска предлагает выполнить 6 рисунков в качестве упражнений для домашних заданий, заметив, что они будут полезны школьникам с гуманитарной направленностью. Там же приведен список изображаемых объектов (зонтик, очки, кит, шахматный король, лягушка, бабочка) и перечень функций, графики которых участвуют в этом изображении. Заметим, что продолжение, в смысле новых рисунков, напечатано в газете “Математика” [2].
О том, как этот материал можно использовать с целью попытки решения тех проблем, которые выделили выше, дальше пойдет речь.
Наш век – век компьютеров, значит, они должны работать и на уроках математики, а не только на уроках информатики. Мы предлагаем воспользоваться программой, по которой возможно выполнить эти 6 рисунков. Программа выполнена в формате интернет-страниц.
Все графики вычерчиваются исходя из математических формул. На экране отображается координатная сетка и оси. При нажатии на изображение уравнения происходит вычерчивание графика, причем это построение можно повторить несколько раз. Размер чертежа можно увеличить или уменьшить, что позволяет уточнить координаты той или иной точки. Программу, выполняющую данные построения, можно найти в Интернете по адресу http://kgpu.real.kamchatka.ru
Приводим наши предложения о том, что можно добавить к материалу при изучении квадратичных функций и как это сделать.
Начнем с фрагмента начала урока перед рассмотрением построения графика квадратичной функции «y=ax2«.
На экране телевизора или компьютера медленно вырисовываются в разных цветах части парабол, которые в итоге дают изображение лягушки.
Учитель замечает, что детали для рисунка предоставила нам очень интересная функция, называемая квадратичной, построение графиков которой – цель нашего урока. После освоения материала (на него уйдет не один урок) каждый сможет сам рисовать, а проверять свои художества можно, используя компьютер. Учитель примерно так вводит учащихся в новую тему.
Какая задумка была у учителя в самом начале урока? Вызвать эмоциональные переживания через удивление. На это работает необычность приводимого факта, красота обозреваемого объекта, скорость получения результата…
В этом случае внутренние переживания ученика подключаются к таким процессам, как запоминание, внимание, осмысливание. Они будут протекать более интенсивно и способствовать достижению решаемых задач в обучении.
В конце урока в качестве итога учитель обращает внимание на материал стенда, который до этого был закрыт “Изучаем на уроке”.
На нем привлекает внимание лягушонок, который запомнился учащимся и держит их в ожидании нового урока. Этого нам очень хотелось бы достичь. Потому приведены все функции, принимавшие участие в выполнении рисунка. Они отличаются от тех, с которыми учащиеся имели дело на прошедшем уроке, что особо подмечал учитель.
Там же запечатлена хроника начала урока с конкретизацией ряда моментов в шутливой стихотворной форме и подчеркнута возможность ученика, усвоившего изучаемый материал, в дальнейшем так же, как компьютер, рисовать графиками функции.
Творчески работающий учитель найдет, где и как использовать при изучении программного материала нижеследующие задания. Они будоражат фантазию, развивают эстетические наклонности, приобщают к поиску, пониманию математических истин, увлекают в загадочный мир знаний.
Задание 1.
1) Построить график функции и сделать трафарет.
2) С помощью трафарета дорисовать построенную параболу до того, на чем остановится Ваша фантазия. При этом трафарет можно переворачивать, перемещать влево или вправо, вверх или вниз, использовать любую его часть и оси координат.
3) Записать формулы парабол, прямых, которые определили Ваш рисунок.
Приводим пример выполнения задания 1. Парабола построена .
После несложных размышлений принято решение рисовать тюльпан. Из параболы получается цветок, если ее прервать, проведя вверху изящную волнистую линию. Ось игреков от точки О вниз – это стебелек, справа и слева от него можно сделать по листочку.
Наши действия: трафарет переворачиваем (т.е. ветви направляем вниз) и перемещаем по параболе…
Находятся такие точки С, D, Е, которые после совмещения (трижды) с точкой О (на трафарете) дадут нужную линию.
Запишем формулы трех парабол, позволившие это сделать. Работает формула , где точка (m; n) — вершина параболы. У нас первая точка С (-4; 19) – вершина одной из парабол, а именно . Мы обводим только участок параболы при . Аналогичным будет подход в описании всех остальных случаев.
В итоге тюльпан рисовали семь квадратичных функций и одна линейная:
1.
2.
3.
4.
5.
6.
7.
8.
Задание 2.
Графиками функций [3] сделать рисунок, дать ему название.
Например. Даны функции:
1.
2.
3.
4.
5.
6.
7.
Учащиеся строят графики, получают рисунок. Если не сделано ошибок, он должен выглядеть так, как показано:
Задание 3.
После завершения работы над заданием 2, проверить правильность его выполнения на компьютере.
Задание 4.
Придумать рисунки, которые создадут графики функций (квадратичной и линейной) и записать эти функции аналитически.
Задание 5.
Выполнить желаемые рисунки (кошка, птица, динозаврик, верблюд, фазан, сидящая кошка, голова женщины, соболь, женщина с ведрами) графиками функций: параболами, прямыми, воспользовавшись материалами, опубликованными в [2].
Задание 6.
Перед Вами ландыш – , рыба — «, лицо клоуна – . Напишите формулы функций, которые их определили, если они выполнены с помощью только трафарета графика функции .
Замечание.
Рисунок ландыша выполнили графики 19 функций, рыбы – 16 функций; над изображением лица клоуна трудились графики 17 функций.
Список литературы
1. Алгебра: Учеб. для 9 кл. общеобразоват. учреждений / Под ред. С.А. Теляковского. – М.: Просвещение, 2002.
2. Цукарь А.Я. Рисуем графиками функций // Математика. – 1999. – № 7, № 22, № 23, № 24, № 25.
3. Цукарь А.Я. Рисуем графиками функций // Математика в школе. – 1999. – № 4. – С. 80-81.
Интересные графики (45 фото)
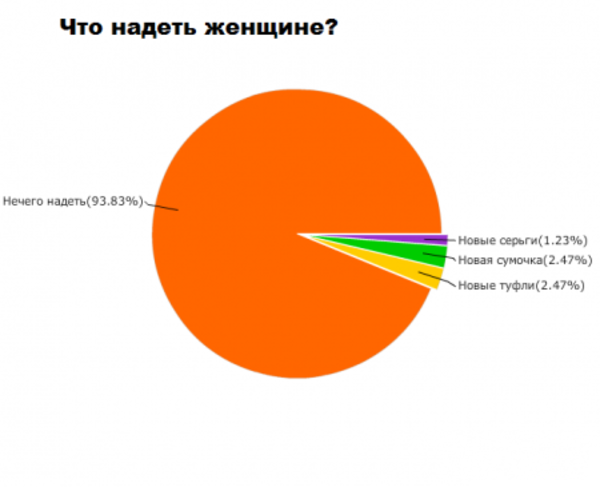
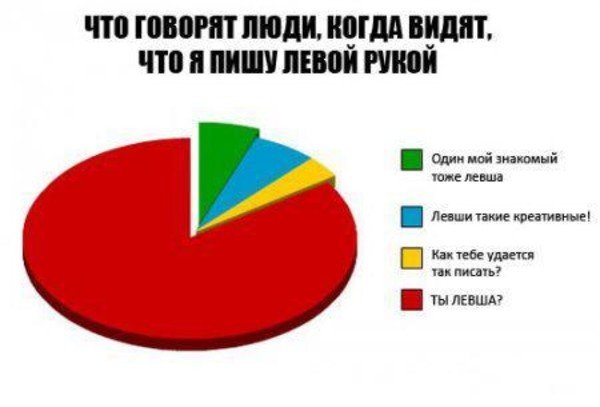
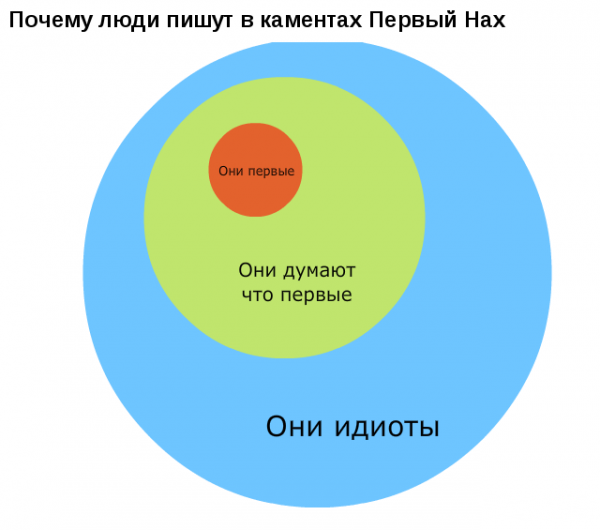
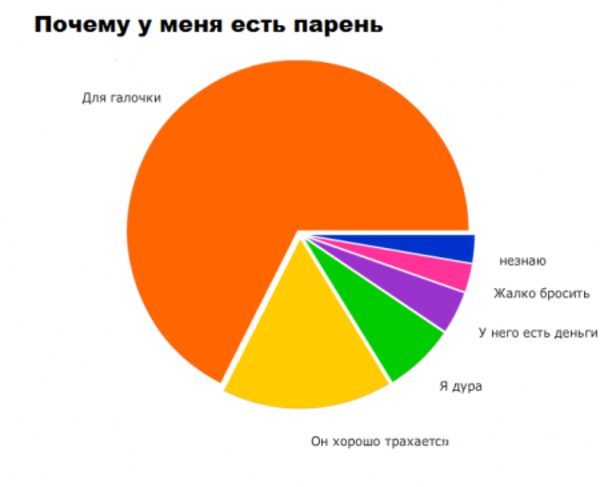
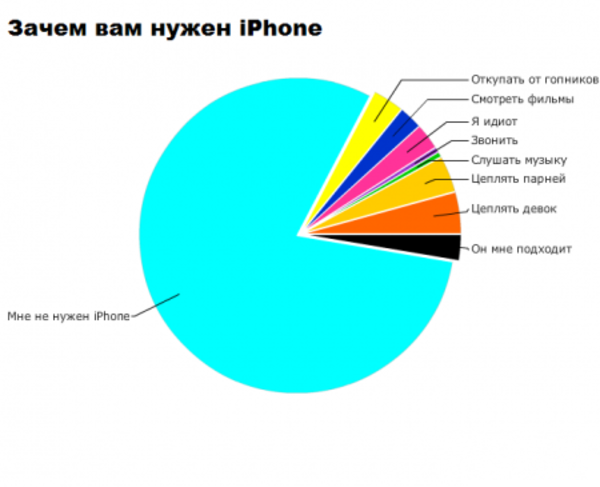
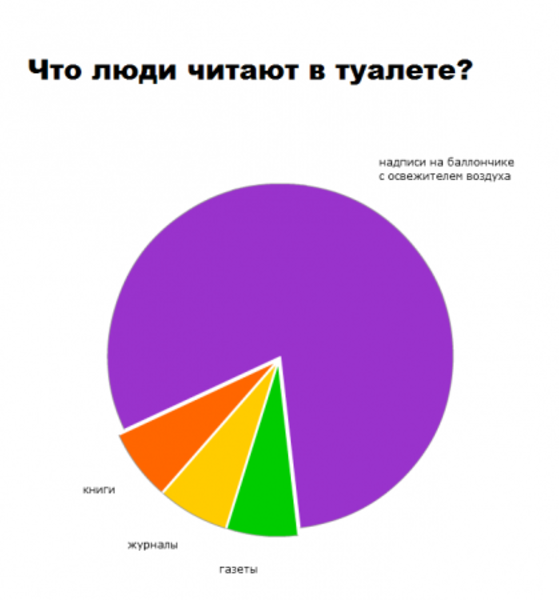
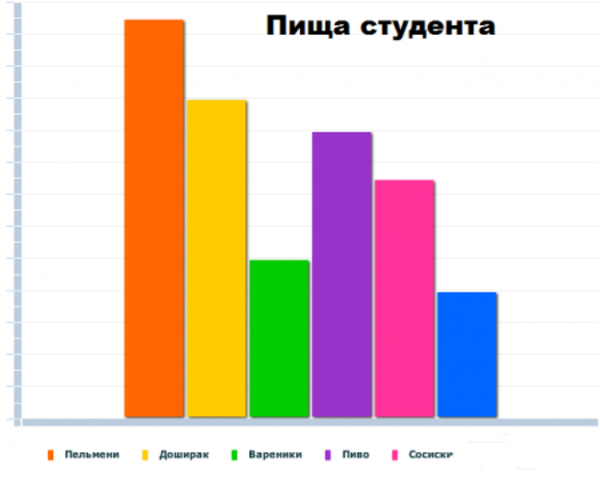
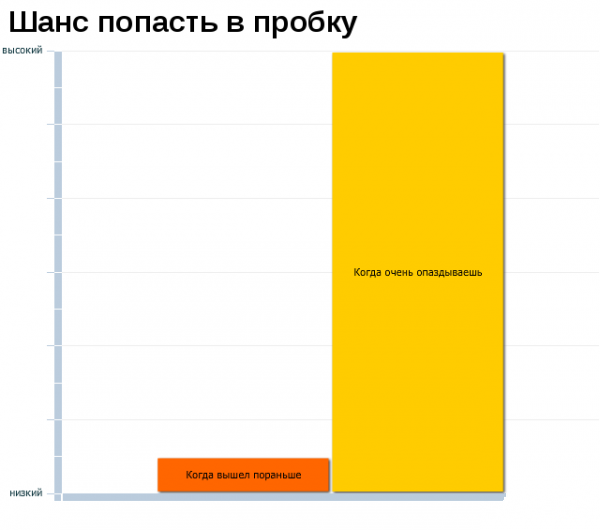
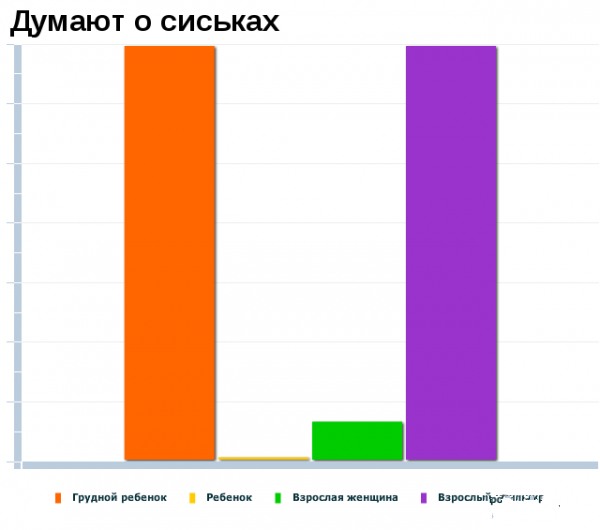
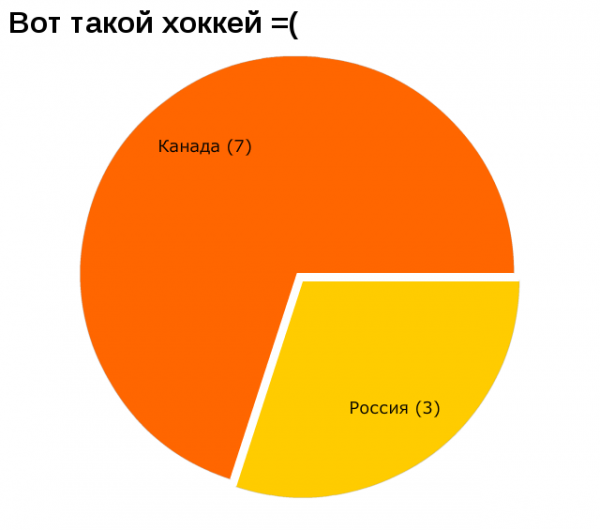
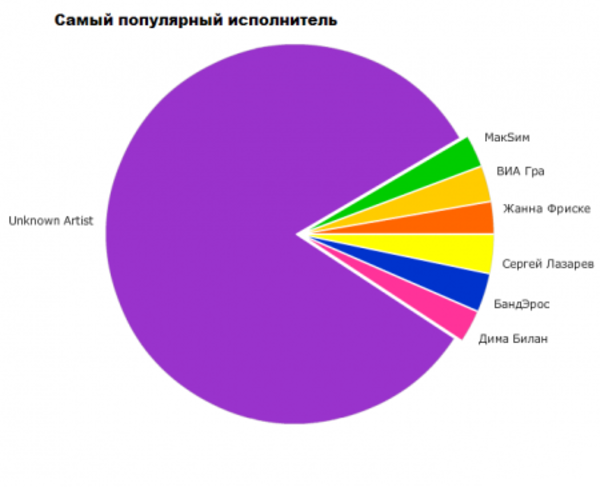
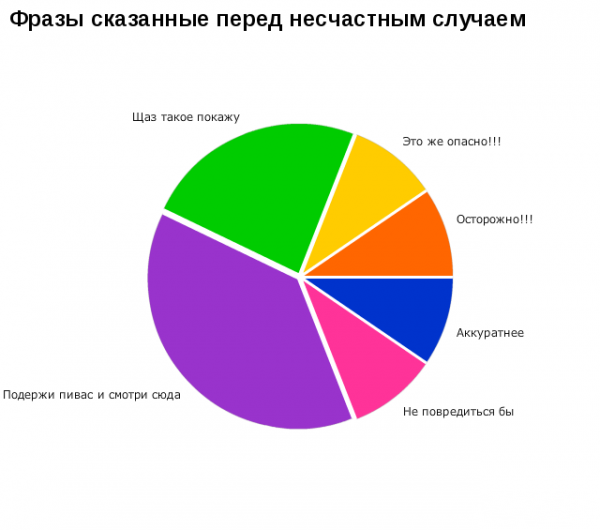
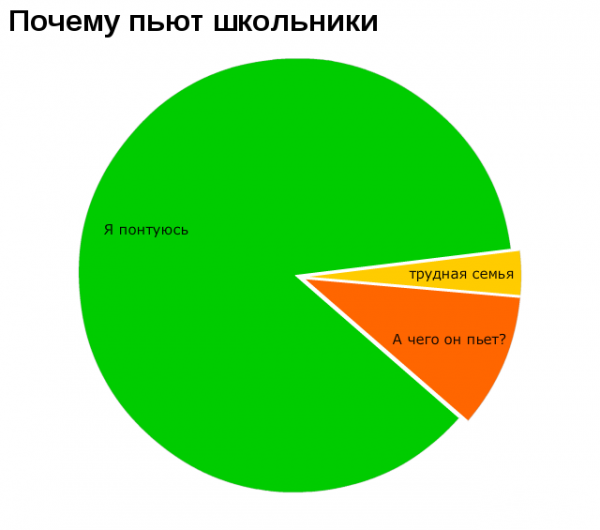
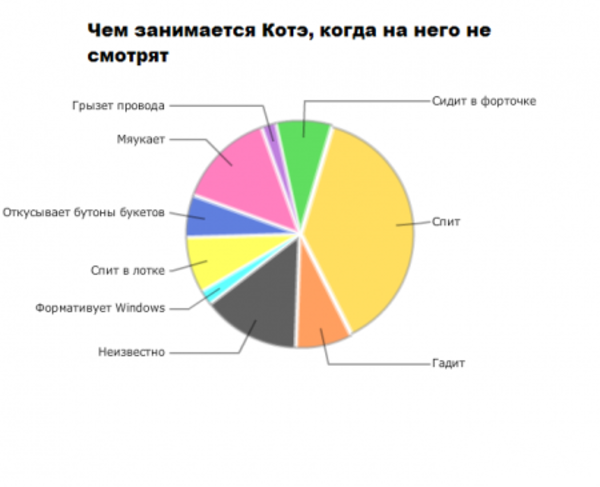
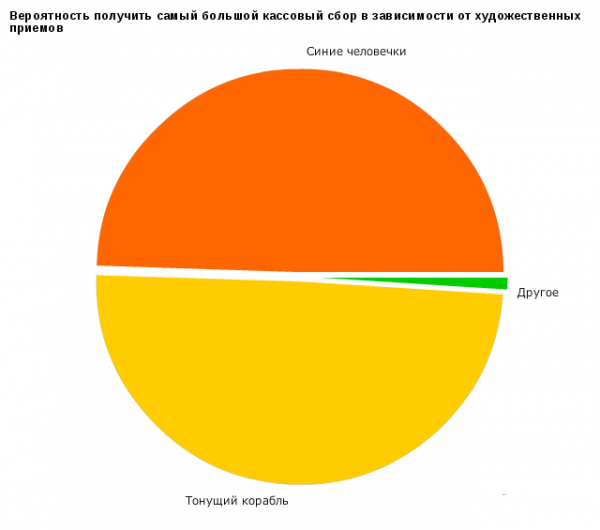
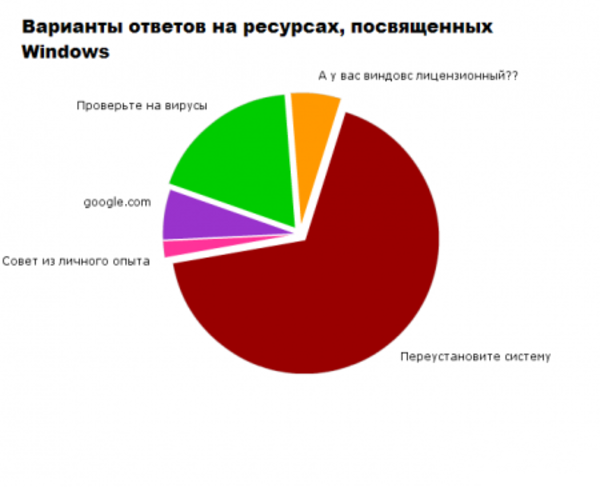
Немного забавной статистики.





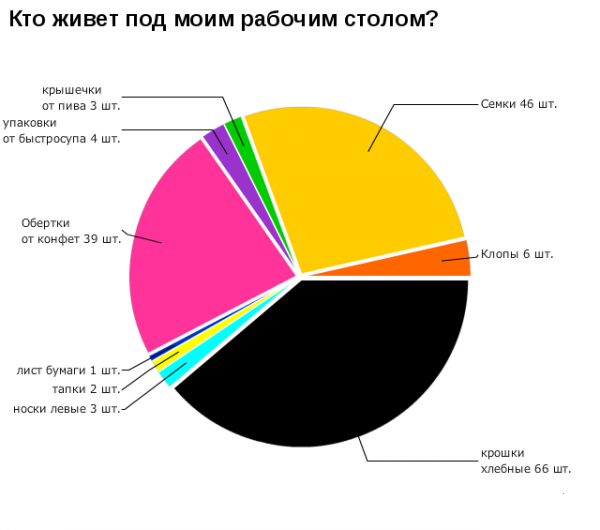

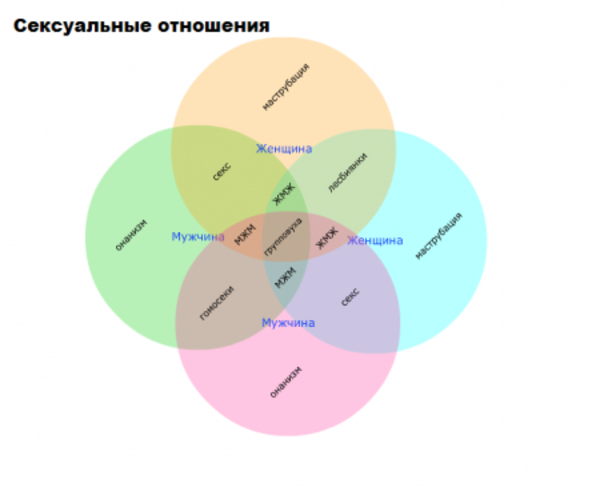
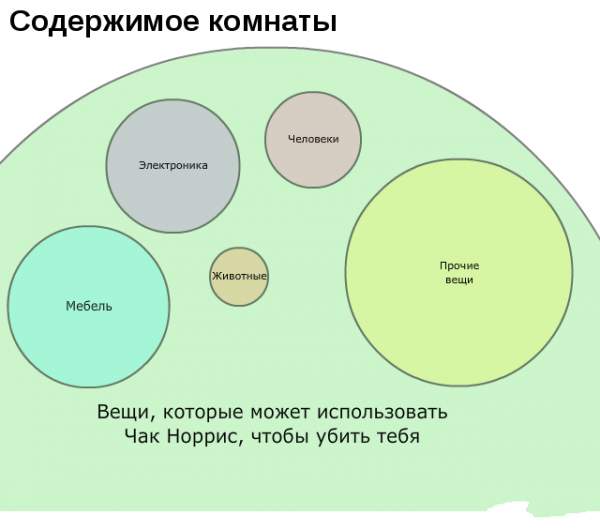

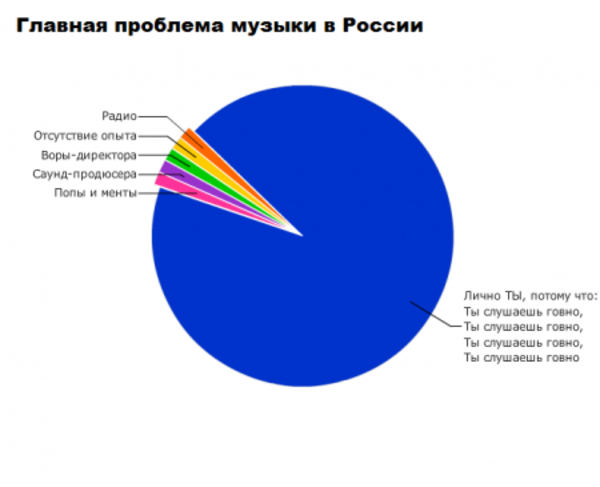
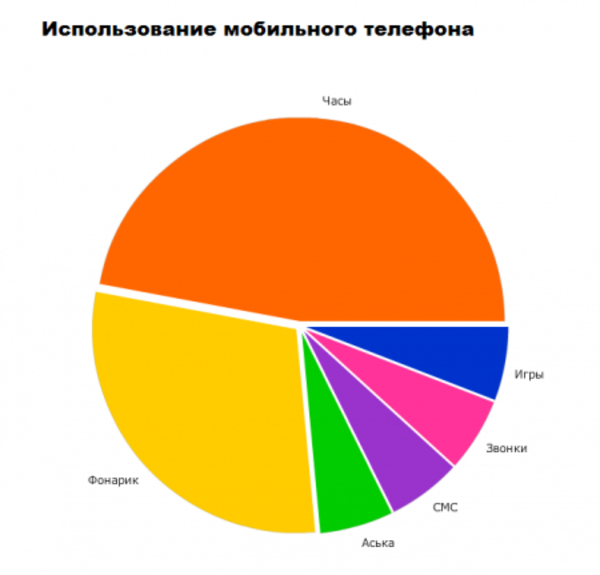

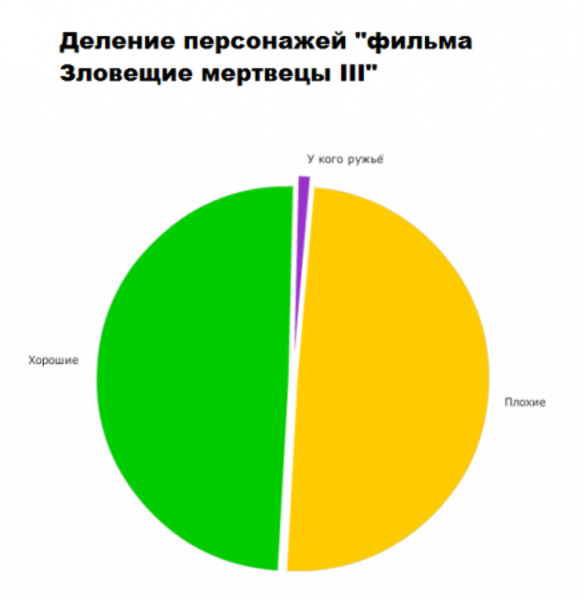
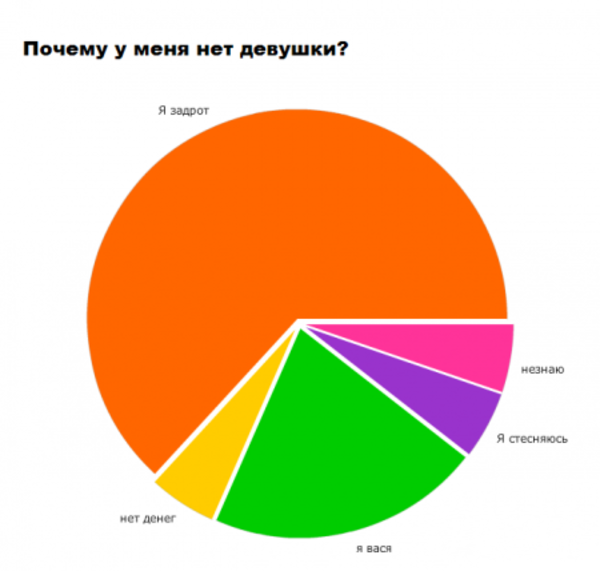
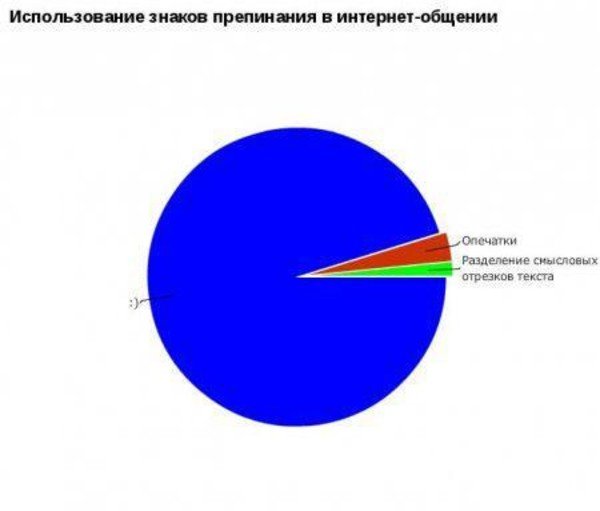

Мы рекомендуем Вам зарегистрироваться либо войти на сайт под своим именем.
Информация
Посетители, находящиеся в группе Гости, не могут оставлять комментарии на Загонах. Зарегистрируйтесь!
Комментарии 17
Режим «Картинка в картинке» на Android — как включить?
Как включить и пользоваться функцией «Картинка в картинке» на смартфонах и планшетах?
Картинка в картинке — удобный режим многозадачности, разработанный в 2017 году. Впервые опция стала доступной для пользователей YouTube, обладающих платными подписками. Впоследствии режим распространился на другие приложения в операционной системе Android. В середине 2018 года необходимость покупки платной подписки YouTube для использования функции Picture-in-Picture исчезла.
Зачем нужен режим «Картинка в картинке»?
Функция «Картинка в картинке» позволяет пользоваться одновременно несколькими приложениями. Например, можно запустить воспроизведение видео в YouTube и открыть любую другую программу. Перед пользователем отобразится небольшое окно, в котором отображается содержимое видеохостинга. При необходимости окно можно перетягивать пальцем и взаимодействовать с интерфейсом. Справа находится кнопка закрытия программы, выполненная в форме символа «X». После нажатия данной клавиши приложение будет закрыто.
Как включить режим «Картинка в картинке»?
Чтобы активировать режим в YouTube, нужно открыть «Общие настройки» и передвинуть переключатель напротив соответствующего пункта. После чего можно открыть интересующее видео и нажать кнопку «Домой». В результате отобразится небольшое плавающее окно, в котором будет проигрываться видео. Важно заметить — режим Picture-in-Picture не поддерживается при воспроизведении некоторых музыкальных клипов. Данная особенность связана с требованиями правообладателей.

Включить режим можно для других приложений, например, Google Maps. Управление настройками осуществляться в меню смартфона. Перейдите в раздел «Приложения и уведомления»— «Расширенные настройки» — «Специальный доступ». Затем выберете пункт «Картинка в картинке». В результате отобразится список всех программ, в которых можно пользоваться соответствующей опцией. Для изменения параметров необходимо передвинуть переключатель на странице программы.
Функция Picture-in-Picture позволяет взаимодействовать одновременно с несколькими программными интерфейсами. Например, пользователь способен переписываться в мессенджере и одновременно просматривать видео. Обратите внимание, что режим пока обладает определенными ограничениями. Невозможно запускать в окне некоторые программы или просматривать отдельные клипы с YouTube. Посмотреть список всех поддерживаемых приложений можно в настройках смартфона.
 Загрузка…
Загрузка…Функция «картинка в картинке». Что это такое?
У современных телевизоров такие технические характеристики, что им нельзя не удивляться. У любой новой модели много технологий, улучшающих качество изображения. И потому смотреть телевизор – одно удовольствие. Далее мы расскажем о такой функции, как «картинка в картинке».Львиная доля современных моделей имеет эту очень полезную технологию. И потому немало пользователей смогло по достоинству оценить то, насколько удобно ею пользоваться. Сразу подчеркнем, что у этой функции есть несколько разновидностей.
Picture in Picture
Эта функция, которую мы сейчас рассмотрим, именно так в оригинале и называется. При дословном переводе это означает «картинка в картинке». В редких случаях можно увидеть сокращенное обозначение функции – PiP.
Обращаем внимание на то, что именно в США примерно полвека назад смогли успешно реализовать такую идею: во время трансляции поделить экран на несколько независимых зон.
Встроенной в телевизор эта функция тогда не была. Телеканал, показывающий спортивные матчи, имел собственную техническую аппаратуру. И за счет нее он мог одновременно взять несколько изображений с разных частей стадиона, чтобы потом вывести их на экраны зрителей.Телезрителю хорошо знакомо это чувство, когда не знаешь, какой канал смотреть? Это такое своеобразное чувство неопределенности. Оно появляется, когда на одном канале показывают любимые мультики, а на втором транслируют соревнования по зимнему двоеборью.
Плюсы и минусы PiP
А ведь проблему-то можно решить, если задействовать именно функцию «картинка в картинке». Ведь она предоставляет возможность вести контроль сразу на нескольких каналах.
Это означает, что функция «картинка в картинке» предоставляет возможность телевизору действовать в специфическом режиме, когда зрителю на экране видно сразу пару картинок. Основная картинка занимает примерно 90% экрана. А еще появляется дополнительное маленькое окошко.
Пользователь может регулировать размер дополнительного окна. Но не только. И место, где оно будет расположено на основном дисплее. Если нужно, то можно с пультом в руках дополнительное и основное изображение менять местами.
У технологии «picture in picture» есть и недостатки. Основной недостаток, пожалуй, в том, что одно изображение всегда будет перекрывать другое. В этом есть своя логика. Однако надо признать, что это не всегда удобно.Есть проблема с выводом звука для изображения. Когда одновременно проводишь озвучивание пары каналов, то смысла в этом нет никакого. Обычно функциональные возможности телевизора таковы, что можно вывести звук только одного изображения. То есть или дополнительного, или основного.
Есть такие модели, в которых предусмотрена возможность передавать звук одновременно по разным каналам. Это может быть, например, разъем для наушников или акустическая система телевизора. Понятно, что это позволяет смотреть один телевизор, не мешая друг другу, сразу двум зрителям.
Функция «картинка в картинке» в телевизоре может быть воплощена по-разному. Все зависит от того, какова техническая составляющая конкретной модели. Сегодня уже делают телевизоры даже с парой встроенных тюнеров.
Успешное применение технологии «picture in picture» возможно в модели с одним тюнером. Однако для этого необходим дополнительный источник видеосигнала. Ведь тюнер принимает лишь один сигнал. Этим дополнительным источником может стать проигрыватель DVD, видеомагнитофон, компьютер. PiP позволяет смотреть фильм по DVD, а в маленьком окошке – телепередачу. Не получится смотреть две передачи на телевизоре с одним тюнером.
Для одновременного просмотра двух телевизионных программ требуется либо внешний тюнер, либо спутниковый ресивер. С ресивером в основном окне смотрят ТВ, а в дополнительном – спутниковую программу. В дорогих телевизорах с двумя тюнерами на одном экране сразу можно принимать несколько сигналов и транслировать несколько каналов.
В моделях телевизоров, поддерживающих функцию Multi PiP, можно вывести самую разную информацию на экран, где много дополнительных окон. Их может быть 16 и больше. Теперь о полезной функции — «мультиэкран», позволяющей выводить на экран изображение с переходом к полноэкранному просмотру.
Picture outside Picture
«Картинка вне картинки», или PoP. Когда используется эта технология, то на экране (в формате 4:3) выводится основное изображение. А в свободной зоне дисплея появляется не черный экран, а дополнительное окошко. В нем – трансляция другого телеканала.
Picture and Picture
«Картинка и картинка», или PaP. Технология делит дисплей на две равные частей. В них – отдельный канал. Эта функция нашла широкое применение в широкоформатных моделях.
Picture and Text
«Картинка и текст», или PaT. Функционально эта технология напоминает предыдущую. Экран также делится на пару частей. Однако на второй половине дисплея не отображение картинки, а телетекст. Значит, можно смотреть любимую передачу и в то же время узнавать свежие новости или получать информацию о том, как изменилась погода.