Диагональ 5 это сколько см: Диагональ телефона 5,5 дюймов — это сколько в сантиметрах? — Эксперт — интернет-магазин электроники и бытовой техники

Содержание

Размеры дисплея смартфона в дюймах, пикселях, сантиметрах

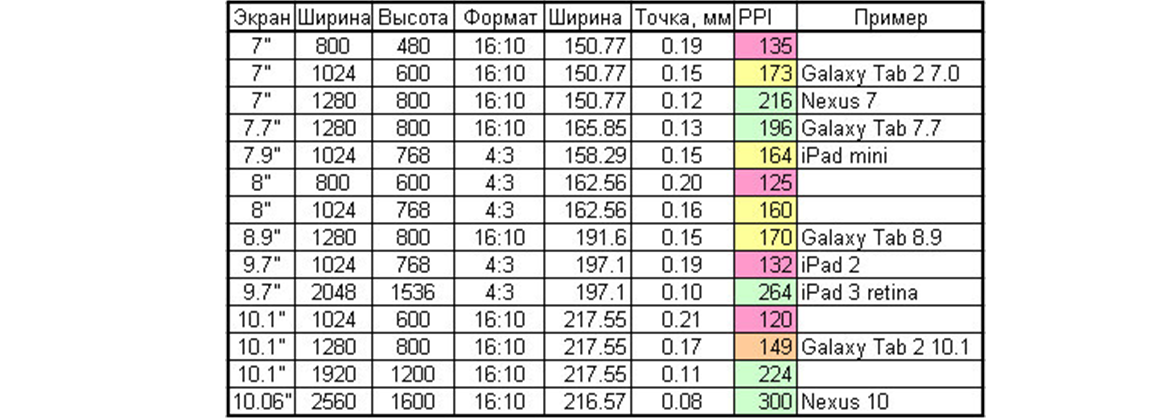
16:9 или 16:10 — соотношение сторон дисплея у основной массы смартфонов. Для описания таких характеристик экрана как диагональ принято использовать дюймы, а если речь идёт о чувствительности — пиксели.

Размеры экранов смартфонов в дюймах

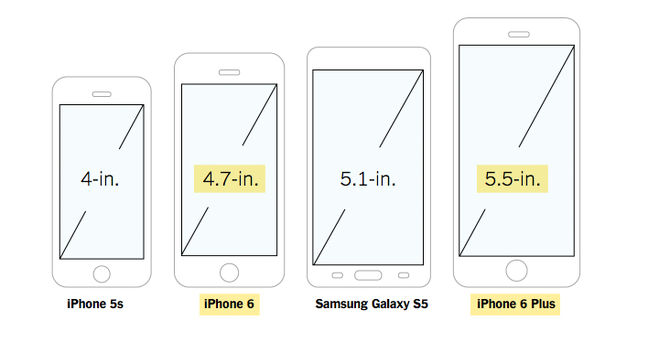
Рост размеров экранов смартфонов — процесс, похоже, непрерывный. Если в 2007 году нормой считалась диагональ равная 3-ём дюймам, то уже в 2012-ом он вырос до 4-ёх дюймов. Если у устройства экран меньше 3”, то его уже не считают смартфоном. Прошло несколько лет и отметка в 5″ уже перестала быть предельной. И изменения этой тенденции, похоже, ждать не стоит. Это объясняется растущей популярностью фаблетов.

Если кто не знает, так фаблетом называют гибрид, составными частями которого являются планшет и смартфон. Ещё их называют плафонами или планшетофонами. Его отличительной чертой является дисплей большого размера, превышающего все среднестатистические девайсы, представленные на рынке.

С ростом диагонали меняется и терминология. Если в 2011 году под определение фаблет подходил Galaxy Note то сегодня так называют исключительно устройства, чей экран имеет диагональ не меньше 5,5 дюймов.

Размылась чёткая грань, разделяющая фаблеты и планшеты. Тут всё зависит от производителей. По классификации Samsung даже Galaxy W, имеющий 7-дюймовый экран — телефон. А Huawei считает, что устройство, имеющее экран такого же размера надо считать мини-планшетом, со встроенным модулем, осуществляющим сотовую связь.

Размеры экранов смартфонов в сантиметрах

Для полного представления о физических размерах матрицы, есть возможность переведения дюймов в более привычные сантиметры, исходя из того, что одному дюйму равны 2, 54 см.

Пиксели в дисплее смартфона

Пиксели не используются для определения физического размера монитора. Ими отображается размер изображения, располагающегося на нём. Говоря о разрешении, имеют в виду количество точек располагающихся как по горизонтали, так и по вертикали.

Этот показатель вкупе с диагональю, измеряемой в дюймах, используется для расчёта плотности пикселей. Высокий показатель гарантирует более чёткую картинку.

Для пользователя, держащего девайс не ближе 30 см от глаз, сложно сконцентрироваться на отдельных точках, если ppi превышает отметку 300. Ещё в 20110 году такая плотность имелась только на Apple, изготовленных по технологии Retina. Однако уже в сегодняшних реалиях даже китайские фаблеты, относящиеся к среднему классу оборудованы экранами FullHD (1920 на 1080 пикселей).

Пятидюймовые смартфоны вполне могут иметь разрешение HD (1280 на 720 точек). Некоторыми производителями устанавливаются на выпускаемые смартфоны дисплеи, имеющие разрешение 2К (2560 на 1440) и 4К (3840 на 2160). Однако пользу от подобных инноваций можно увидеть только при ознакомлении с VR контентом.

Почему так важен размер экрана?

От него зависят габариты устройства. Но при этом девайс, даже имея большой экран, может иметь небольшую толщину.

В этом плане рекордсменом считается Vivo X5 Max, имеющий толщину 4,75 мм. Кроме того от величины экрана в прямой зависимости находится ширина корпуса. Фаблет позволяет со всеми удобствами просматривать фильмы, осуществлять наборы текста и серфинговать на просторах интернета.

И всё это при меньших, относительно планшета размерах. И к тому же он всегда в пределах досягаемости. Так думают и пользователи. Об этом говорит падение спроса на iPad после того, как был презентован первый планшет Apple. Оно составило 13% по результатам 4-го квартала 2014 года.

Есть ли у фаблетов минусы? Конечно. Их появление сделало невозможным одноручное управление смартфонном. Большому пальцу не удаётся достать все зоны экрана, если не выполнять перехват. А значит, создаются неудобства для пользования на ходу. И избавиться от этого неудобства можно только уменьшением полезной площади экрана.

В iOS есть возможность сдвинуть вниз интерфейс. Для этого выполняется двойной клик на Home — кнопки, на которой изображён логотип, принадлежащий системе. Благодаря особенностям некоторых ОС Android есть возможность одним жестом выполнить включение управление посредством руки.

От размера, который имеется у экрана, в прямой зависимости находится выбор смартфона. Предложение определяется трендом. Именно по этой причине в текущем году пользователи с непониманием воспринимают флагманские смартфоны, чей экран меньше 5,2 дюйма. В качестве исключения можно назвать iPhone и устройства, относящиеся к семейству Sony Xperia Z Compact. По некоторым сведениям компании планируют представлять модели, размер экрана которого будет равен 5 дюймам, и процессором А8.

Немалое значение уделяется соотношению между габаритами дисплея и величиной корпуса гаджета (screen-to-body ratio). Обладая диагональю в 5,7 дюйма, Xiaomi Mi Note имеет меньшие размеры, чем iPhone 6s Plus. Использование узких рамок, окаймляющих дисплей, является одной из самых популярных тенденций. Когда речь идёт о вопросах, связанных с конструированием смартфонов в предыдущем году.

И дело тут исключительно в эстетике.

Параллелограмм – свойства, признаки, определение

Научим решать сложные задачи о параллелограммах

Начать учиться

Геометрические фигуры изучают не только восьмиклассники и технари, но и представители творческих специальностей. Нестандартные четырехугольные формы можно встретить как в дизайне обуви, так и в современных зданиях. В этой статье расскажем о параллелограмме и его отличительных особенностях.

Определение параллелограмма

Параллелограмм — это четырехугольник, у которого противоположные стороны попарно параллельны и равны. Как выглядит параллелограмм:

Частные случаи параллелограмма: ромб, прямоугольник, квадрат.

Диагонали — отрезки, которые соединяют противоположные вершины.

Свойства диагоналей параллелограмма:

В параллелограмме точка пересечения диагоналей делит их пополам.

Любая диагональ параллелограмма делит его на два равных треугольника.

Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон.

Биссектриса угла параллелограмма — это отрезок, который соединяет вершину с точкой на одной из двух противоположных сторон и делит угол при вершине пополам.

Свойства биссектрисы параллелограмма:

Биссектриса параллелограмма отсекает от него равнобедренный треугольник.

Биссектрисы углов, прилежащих к одной стороне параллелограмма пересекаются под прямым углом.

Отрезки биссектрис противоположных углов равны и параллельны.

Как найти площадь параллелограмма:

S = a × h, где a — сторона, h — высота.

S = a × b × sinα, где a и b — две стороны, sinα — синус угла между ними. Для ромба формула примет вид S = a² × sinα.

Для ромба: S = 0,5 × (d1 × d2), где d1 и d2 — две диагонали.
Для параллелограмма: S = 0,5 × (d1 × d2) × sinβ, где β — угол между диагоналями.

Периметр параллелограмма — сумма длины и ширины, умноженная на два.

P = 2 × (a + b), где a — ширина, b — высота.

У нас есть отличные дополнительные курсы по математике для учеников с 1 по 11 классы!

Реши домашку по математике на 5.

Подробные решения помогут разобраться в самой сложной теме.

Свойства параллелограмма

Геометрическая фигура — это любое множество точек. У каждой фигуры есть свои свойства, которые отличают их между собой и помогают решать задачи по геометрии в 8 классе.

Рассмотрим основные свойства диагоналей и углов параллелограмма, узнаем чему равна сумма углов параллелограмма и другие особенности этой фигуры. Вот они:

Противоположные стороны параллелограмма равны.
ABCD — параллелограмм, значит, AB = DC, BC = AD.

Противоположные углы параллелограмма равны.
ABCD — параллелограмм, значит, ∠A = ∠C, ∠B = ∠D.

Диагонали параллелограмма точкой пересечения делятся пополам.
ABCD — параллелограмм, AC и BD — диагонали, AC∩BD=O, значит, BO = OD, AO = OC.

Диагональ делит параллелограмм на два равных треугольника.
ABCD — параллелограмм, AC — диагональ, значит, △ABC = △CDA.

Сумма углов в параллелограмме, прилежащих к одной стороне, равна 180 градусам.
ABCD — параллелограмм, значит, ∠A + ∠D = 180°.

В параллелограмме диагонали d1, d2 и стороны a, b связаны следующим соотношением: d1² + d2² = 2 × (a² + b² ).

А сейчас докажем теорему, которая основана на первых двух свойствах.

Теорема 1. В параллелограмме противоположные стороны и противоположные углы равны.

В любом выпуклом четырехугольнике диагонали пересекаются. Все, что мы знаем о точке их пересечения — это то, что она лежит внутри четырехугольника.

Если мы проведем обе диагонали в параллелограмме, точка пересечения разделит их пополам. Убедимся, так ли это:

AB = CD как противоположные стороны параллелограмма.

∠1 = ∠2 как накрест лежащие углы при пересечении секущей AC параллельных прямых AB и CD; ∠3 = ∠4 как накрест лежащие углы при пересечении секущей BD параллельных прямых AB и CD.

Следовательно, треугольник AOB равен треугольнику COD по второму признаку равенства треугольников, то есть по стороне и прилежащим к ней углам, из чего следует:
- CO = AO
- BO = DO

Теорема доказана.

Наше предположение верно.

Признаки параллелограмма

Признаки параллелограмма помогают распознать эту фигуру среди других четырехугольников. Сформулируем три основных признака.

Первый признак параллелограмма. Если в четырехугольнике две противолежащие стороны равны и параллельны, то этот четырехугольник — параллелограмм.

Докажем 1 признак параллелограмма:

Шаг 1. Пусть в четырехугольнике ABCD:

AB || CD
AB = CD

Чтобы назвать этот четырехугольник параллелограммом, нужно внимательно рассмотреть его стороны.

Сейчас мы видим одну пару параллельных сторон. Нужно доказать, что вторая пара сторон тоже параллельна.

Шаг 2. Проведем диагональ. Получились два треугольника ABC и CDA, которые равны по первому признаку равенства, то есть по по двум сторонам и углу между ними:

AC — общая сторона;

По условию AB = CD;

∠1 = ∠2 как внутренние накрест лежащие углы при пересечении параллельных прямых AB и CD секущей АС.

Шаг 3. Из равенства треугольников также следует:

∠3 = ∠4

Эти углы тоже являются внутренними накрест лежащими для прямых CB и AD. А это как раз и есть признак параллельности прямых. Значит, CB || AD и ABCD — параллелограмм.

Вот так быстро мы доказали первый признак.

Второй признак параллелограмма. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.

Докажем 2 признак параллелограмма:

Шаг 1. Пусть в четырехугольнике ABCD:

AB = CD
BC = AD

Шаг 2. Проведем диагональ AC и рассмотрим треугольники ABC и CDA:

AC — общая сторона;
AB = CD по условию;
BC = AD по условию.

Из этого следует, что треугольники ABC и CDA равны по третьему признаку, а именно по трем сторонам.

Шаг 3. Из равенства треугольников следует:

∠ DCA = ∠BAC
А так как эти углы — накрест лежащие при сторонах BC и AD и диагонали AC, значит, стороны BC и AD параллельны.
∠DAC = ∠BCA
Эти углы — накрест лежащие при сторонах AB и CD и секущей AC. Поэтому стороны AB и CD тоже параллельны. Значит, четырехугольник ABCD — параллелограмм, ЧТД.

Доказали второй признак.

Третий признак параллелограмма. Если в четырехугольнике диагонали точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.

Докажем 3 признак параллелограмма:

Шаг 1. Если диагонали четырехугольника ABCD делятся пополам точкой O, то треугольник AOB равен треугольнику COD по двум сторонам и углу между ними:

CO = OA;
DO = BO;
углы между ними равны, как вертикальные, то есть угол AOB равен углу COD.

Шаг 2. Из равенства треугольников следует, что CD = AB.

Эти стороны параллельны CD || AB, по равенству накрест лежащих углов: ∠1 = ∠2 (следует из равенства треугольников AOB и COD).

Значит, ABCD является параллелограммом по первому признаку, который мы доказали ранее. Что и требовалось доказать.

Теперь мы знаем свойства параллелограмма и то, что выделяет его среди других четырехугольников — признаки. Так как они совпадают, эти формулировки можно использовать для определения параллелограмма. Но самое распространенное определение все-таки связано с параллельностью противоположных сторон.

Шпаргалки для родителей по математике

Все формулы по математике под рукой

Лидия Казанцева

Автор Skysmart

К предыдущей статье

414.4K

Натуральные числа

К следующей статье

302. 8K

Обыкновенные дроби

Получите план обучения, который поможет понять и полюбить геометрию

Премиум

На вводном уроке с методистом

Проверим знание геометрии и других разделов математики, выявим пробелы
Подберём курс
Познакомим с интерактивной платформой

Если диагонали ромба равны 12 см и 16 см, найдите длину каждой стороны…

Перейти к

Понимание фигур. Специальные типы четырехугольников. Упражнение 17.1.
Понимание фигур. Специальные типы четырехугольников. Упражнение 17.2.
Понимание фигур. Специальные типы четырехугольников. Упражнение 17.3.

Рациональное число
Полномочия
Квадраты и квадратные корни
Куб и кубические корни
Игра с числами
Алгебраические выражения и тождества
Факторизация
Отдел алгебраических выражений
Линейное уравнение с одной переменной
Прямые и обратные варианты
Время и работа
Процент
Скидка на убыток и налог на добавленную стоимость
Сложные проценты
Понимание многоугольников фигур
Понимание фигур Четырехугольники
Понимание фигур Специальные типы четырехугольников
Практическая геометрия
Визуализация фигур
Площадь трапеции и многоугольника
Объем Площадь Прямоугольный Куб
Площадь поверхности и объем правого кругового цилиндра
Классификация и табулирование данных
Классификация и табулирование данных Графическое представление данных в виде гистограмм
Графическое представление данных в виде круговых диаграмм или круговых диаграмм
Вероятность обработки данных
Введение в графики

Главная > РД Шарма Решения Класс 8 Математика > Глава 17. Понимание фигур. Специальные типы четырехугольников. > Понимание фигур. Специальные типы четырехугольников. Упражнение 17.2. > Вопрос 6

Вопрос 6 Понимание фигур Особые типы четырехугольников Упражнение 17.2

Если диагонали ромба равны 12 см и 16 см, найдите длину каждая сторона.

Ответ:

Мы знаем в диагонали ромба пересекаются под прямым углом пополам.

In ΔAOB

AO = 12/2 = 6 см, BO = 16/2 = 8 см

Использование теоремы Пифагора в ΔAOB

AB2 = AO2 + BO2

AB2 = 62+ 82

AB2 = 36 + 64

AB2 = 100

AB =√100 = 10см

∴Каждая сторона ромба равна 10см.

Стенограмма видео

«Здравствуйте, дети, добро пожаловать на небольшое домашнее задание. И вот вопрос, связанный с ромбом. Вопрос в том, если диагонали арки ромба, ну сантиметр и 16 сантиметров найти длину каждой стороны здесь. ABCD — это ромб. Хорошо, посмотрите артефакты IMDb, прежде чем мы начнем, это будет трудно понять очень важное свойство ромба, которое заключается в том, что диагонали ромба перпендикулярны и делят друг друга пополам. Это заданный вопрос. У нас есть длина диагонали как допустим 12 сантиметров и 16 сантиметров.Вся длина это длина диагонали 12 сантиметров.Тогда каждая из них будет 6 сантиметров.Это будет 6 сантиметров.Так же будет 6 сантиметров.Если мы возьмем другую диагональ то DB равно 16 сантиметрам, тогда Dio будет 8 сантиметрам, а OB будет 8 сантиметрам, так как здесь диагональ делит пополам, поэтому мы можем написать это здесь. АС равен 12 сантиметрам ДБ равна 16 сантиметрам, отсюда. Можно сказать, что ты — половина моря. Эта диагональ, делящая пополам оао, становится половиной АС, поэтому она будет равна половине 12 сантиметров, что равно 6 сантиметрам. Точно так же OB или Bo будут равны половине TB. Это Бо — половина чая. Таким образом, это будет равно Половина от 15, что равно 8 сантиметрам. Теперь мы также знаем, что диагонали ромба здесь являются перпендикулярными приемами пищи. это 90 градусов, поэтому здесь можно применить теорему Пифагора. Так Угол входа aob Применим теорему Пифагора, тогда квадрат a b будет равен квадрату a0 + квадрату OB. Квадрат EB будет равен записи значения Mu, равной 6, поэтому 6 квадратов + значение OB. У нас получилось 8 это будет 8 кв. Квадрат A b равен 36 плюс 64? Так отсюда А б квадрат 400 У нас будет квадратный корень из которого будет равен. Надеюсь, вы поняли, как мы решили эту задачу, применив здесь свойство и применив свойства ромба. Мы использовали теорему Пифагора, чтобы получить этот ответ. Если у вас есть какие-либо вопросы, оставьте комментарий ниже и подпишитесь на этот канал, чтобы увидеть больше видео. Большое спасибо за просмотр.»

Связанные вопросы

Какие из следующих утверждений верны для ромба? (i) Он имеет две пары параллельных сторон. (ii…

Заполните пропуски в каждом из следующих так, чтобы утверждение было верным: (i) Ромб — это па…

Диагонали параллелограмма не перпендикулярны, это ромб? Почему или почему нет?

Диагонали четырехугольника перпендикулярны друг другу. Всегда ли такой четырехугольник является р…

ABCD — ромб. Если ∠ACB = 40°, найдите ∠ADB.

Постройте ромб, диагонали которого равны 10 см и 6 см.

Фейсбук WhatsApp

Копировать ссылку

Было ли это полезно?

Упражнения.

Рациональные числа

Степени

Квадраты и квадратные корни

Куб и Кубические корни

Игра с числами

Алгебраические выражения и тождества

Факторизация

Деление алгебраических выражений

Линейное уравнение с одной переменной

Прямые и обратные вариации

900 02 Время и труд

Процент

Скидка на убыток и налог на добавленную стоимость

Сложные проценты

Понимание фигур, многоугольников

Понимание фигур, четырехугольников

Понимание фигур, специальных типов четырехугольников

Практическая геометрия

Визуализация фигур

Площадь трапеции и многоугольника

Объемная площадь поверхности прямоугольного куба

Площадь поверхности и объем прямого кругового цилиндра

Классификация и табулирование данных

Классификация и табулирование данных Графическое представление данных В виде гистограмм

Графическое представление данных в виде круговых диаграмм или круговых диаграмм

Вероятность обработки данных

Введение в графики

Курсы

Быстрые ссылки

Условия и политика

Как найти длину прямоугольника, длина диагонали которого равна 10 см, а ширина равна 5 см?

Алгебра

Наука

Анатомия и физиология
астрономия
Астрофизика
Биология
Химия
наука о планете Земля
Наука об окружающей среде
Органическая химия
Физика

Математика

Алгебра
Исчисление
Геометрия
Преалгебра
Предварительный расчет
Статистика
Тригонометрия

Гуманитарные науки

Английская грамматика
История США
Всемирная история